本文最后更新于:2024年5月7日 下午
本文简要总结之前傅里叶变换系列文章,梳理脉络,总结应用场景。
课件展示
理论基础
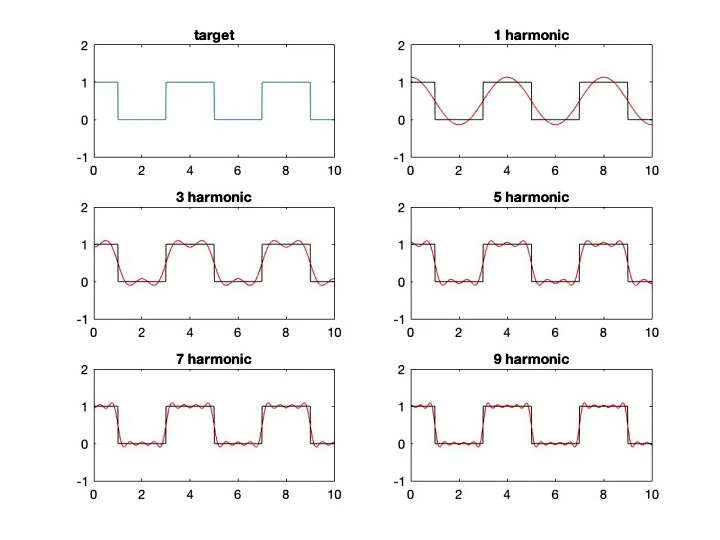
傅里叶级数
- 对周期信号进行分解的方式
$$
\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos \frac{n \pi x}{l}+b_{n} \sin \frac{n \pi x}{l}\right) , l>0, n=1,2, \cdots
$$
$\frac{a_{0}}{2}$ 直流分量,$n$ 为使用的正弦波的下标, $a_n,b_n$ 为幅度
傅里叶级数正交性
$$
\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos \frac{n \pi x}{l}+b_{n} \sin \frac{n \pi x}{l}\right) , l>0, n=1,2, \cdots
$$
- 不同频率的正弦波在任意 $2l$ 周期内积分为 0
- 证明:需要证明 cos sin 两两之间的积分为零,因为道理相同,这里以 cos cos 为例:
时域信号基
- 对于自然界存在的信号,在时域时可以理解为此信号的基为不同时刻的冲击函数,基是一族冲击激信号 $ {\delta(x-n)} $
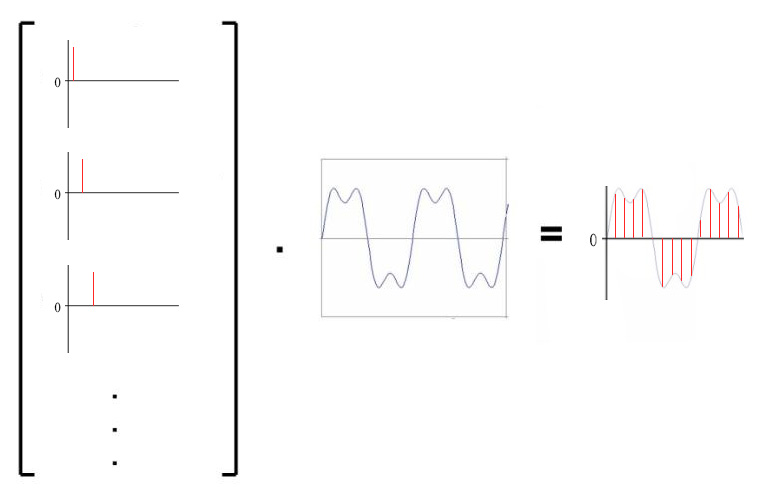
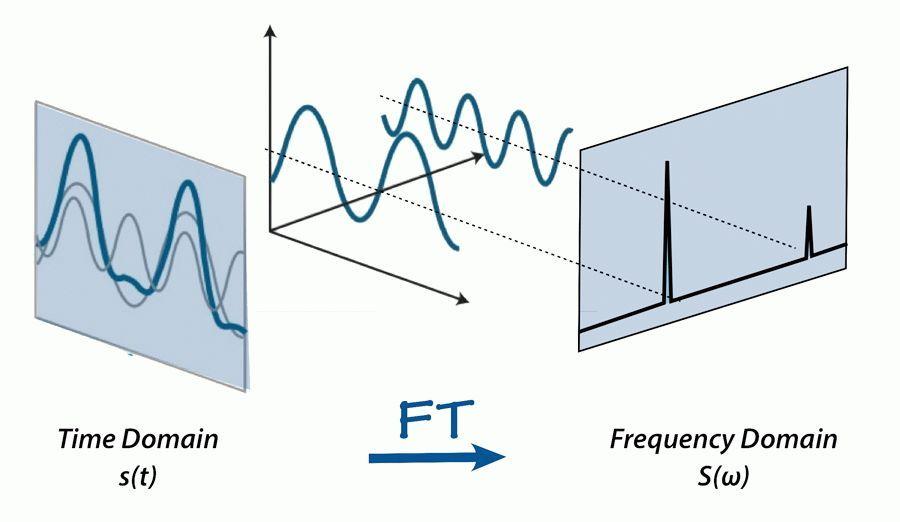
傅立叶变换
-
傅立叶变换是一种基于傅里叶级数的分析信号的方法, 用正弦波作为信号的成分。
-
当选择无限个不同频率不同振幅的正弦、余弦波的集合作为信号的基时, 信号就转换到了频域。
-
在频域中,基是 $ \left\{e^{j w x}\right\} $ ,而且这组基是正交基(基于傅里叶级数)
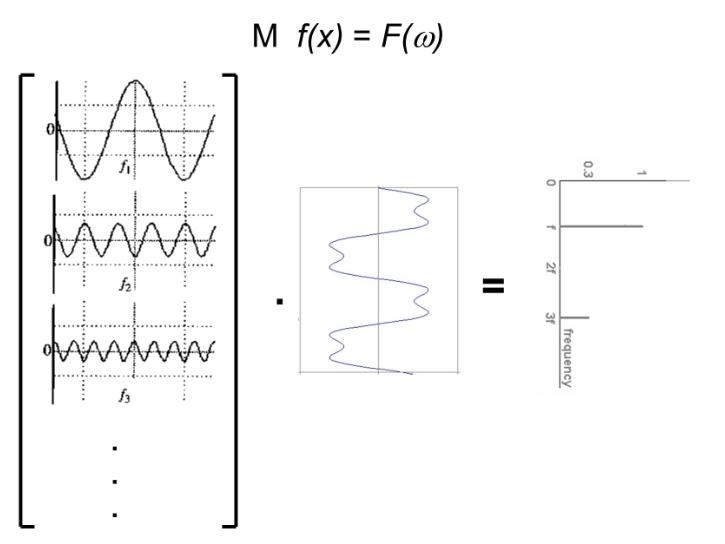
一维傅里叶变换
- $f(x)$ 为时域信号,一维傅里叶变换的定义为:
$$
F(w)=\int_{-\infty}^{+\infty} f(x) e^{-j w x} d x
$$
-
$ F(\omega) $ 叫做 $ {f}(\mathrm{t}) $ 的象函数, $ {f}({t}) $ 叫做$ {F}(\omega) $ 的象原函数。
$ F (\omega) $ 是 $ {f}(\mathrm{t}) $ 的象, $ \mathrm{f}({t}) $ 是$F(\omega)$原象。
-
一维傅里叶变换是将一个一维的信号分解成若干个复指数波 $ e^{j w x} $ 。而由于 $ e^{j w x}=\cos (w x)+i \sin (w x) $ ,所以可以将每一个复指数波 $ e^{j w x} $ 都视为是 $余弦波 +\mathrm{j} {\times} 正弦波$ 的组合。
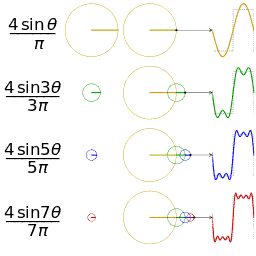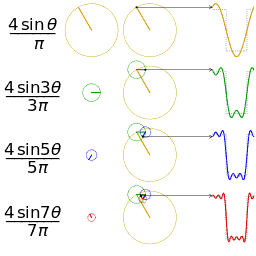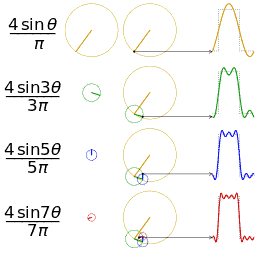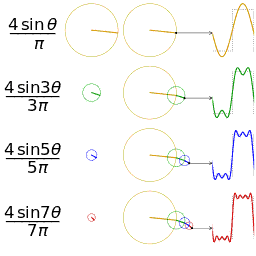
一维傅里叶反变换
- 傅里叶变换可以通过逆变换将象函数变换为象原函数
$$
f(t)=\mathcal{F}^{-1}[F(\omega)]=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{i w t} d \omega
$$
- 证明:
一维傅里叶变换中的正弦波表示
- 对于一个正弦波而言,需要三个参数来确定它:
- 频率 $w$ ,幅度 $A$ ,相位 $φ$
- 因此在频域中,一维坐标代表频率,而每个坐标对应的函数值也就是 $F(w)$ 是一个复数,其中它的幅度 $|F(w)|$ 就是这个频率正弦波的幅度 $A$ ,相位 $∠F(w)$ 就是 $φ$ 。
- 右侧展现的是幅度图,在信号处理中用到更多的也是幅度图。
一维离散傅里叶变换
- 设 $x(n)$ 是一个长度为 $M$ 的有限长序列,则定义 $x(n)$ 的 $N$ 点离散傅里叶变换为
$$
X(k)=\operatorname{DFT}[x(n)]=\sum_{n=0}^{N-1} x(n) W_{N}^{k n} \quad k=0,1, \cdots, N-1
$$
- $X(k)$ 的离散傅里叶逆变换(Inverse Discrete Fourier Transform, IDFT)为
$$
x(n)=\operatorname{IDFT}[X(k)]=\frac{1}{N} \sum_{k=0}^{N-1} X(k) W_{N}^{-k n} \quad n=0,1, \cdots, N-1
$$
式中, $W_{N}=\mathrm{e}^{-j\frac{2\pi}{N}}, N$ 称为 $\mathrm{DFT}$ 变换区间长度, $(N \geqslant M)$ 通常称上述两式为离散傅里叶变换对。
二维傅里叶变换
- 一维信号是一个序列,傅里叶变换将其分解成若干个一维的正弦函数之和。
- 二维傅里叶变换将一个图像分解成若干个复平面波 $ e^{j 2 \pi(u x+v y)} $ 之和。
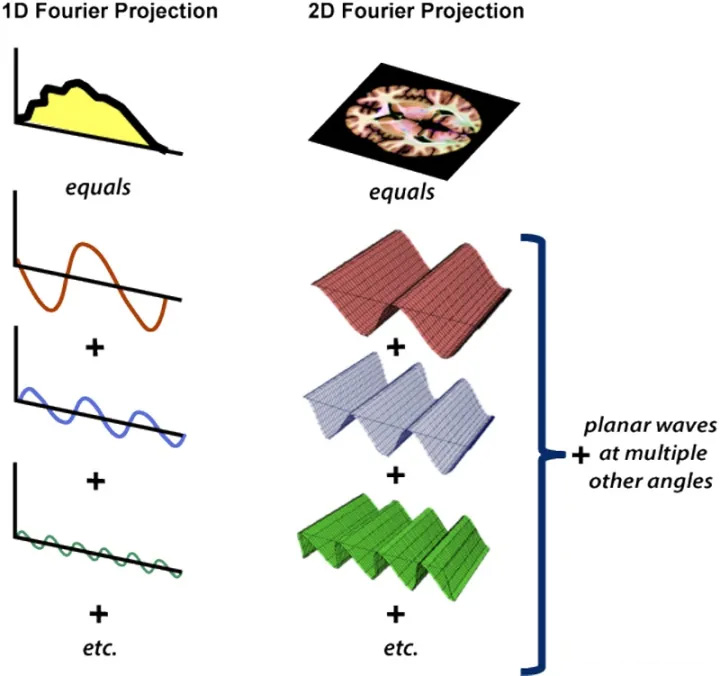
- 对于正弦平面波,可以这样理解,在一个方向上存在一个正弦函数,在法线方向上将其拉伸。前面 说过三个参数可以确定一个一维的正弦波。哪几个参数可以确定一个二维的正弦平面波呢?
- 答案是 四个,其中三个和一维的情况一样 (频率 $ w $, 幅度 $ A $ ,相位 $ \varphi $ ),但是具有相同这些参数的平面波 却可以有不同的方向 $ \vec{n} $ 。
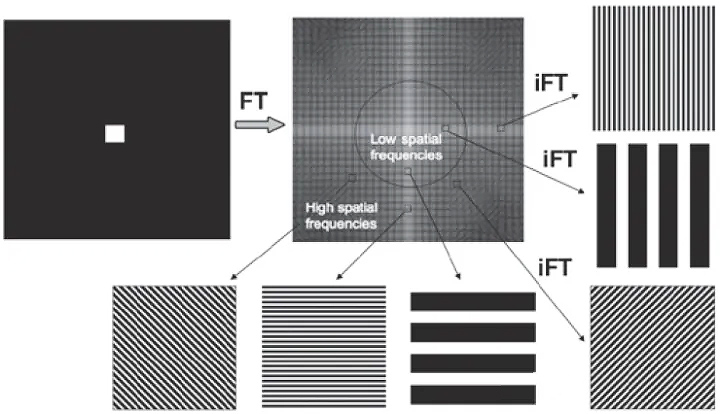
二维连续傅里叶变换
- $f(x, y) $ 为二维时域信号,二维连续傅里叶变换公式为:
$$
F(u, v)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) e^{-j 2 \pi(u x+v y)} d x d y
$$
- 通过公式,我们可以计算出,每个平面波在图像中成分是多少。
- 从公式也可以看到,二维傅里叶变换就是将图像与每个不同频率的不同方向的复平面波做内积,也就是一个求在基 $ \left\{e^{-j 2 \pi(u x+v y)}\right\} $ 上的投影的过程。
二维离散傅里叶变换
-
令 $f(x, y)$表示一幅大小为 $M\times N$像素的数字图像,其中 $x=0,1,2,…,M-1,y=0,1,2,…,N-1$。
-
其二维离散傅里叶变换(DFT)为:
$$
F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) e^{-j 2 \pi(u x / M+v y / N)}
$$
- 离散傅里叶反变换(IDFT)为:
$$
f(x, y)=\frac{1}{M N} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) e^{j 2 \pi(u x / M+v y / N)}
$$
频域乘法代替空域卷积
-
频域是时域整体的表达,频域上信号的一个点,对应的是整个时域信号该对应频率的信息
-
因此,在频域中的乘法,自然就对应了时域整段所有不同频率信号乘法的叠加,这就相当于计算了时域卷积
-
频域乘法理论上可以代替空域卷积运算
卷积 与 互相关 (概念澄清)
- 神经网络的卷积介绍中经常可以看到这样的示意图,称之为卷积
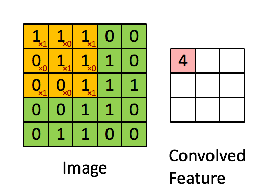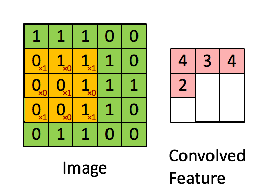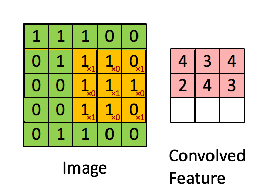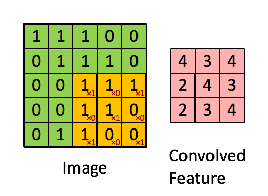
- 在信号处理中的卷积定义为:
$$
S(i, j)=(I * K)(i, j)=\sum \sum I(m, n) K(i-m, j-n)
$$
也就是说 $K$ 的二维信号是左右、上下翻转后再平移求向量点积的,与神经网络中表示的卷积概念有一点出入,只是在不同场合的说法不同。
- 这样设计的好处是使得卷积操作拥有了可交换性,即上式可以等价地写作:
$$
S(i, j)=(K * I)(i, j)=\sum \sum I(i-m, j-n) K(m, n)
$$
- 在信号处理中有一个概念叫互相关, 定义为:
$$
S(i, j)=(I * K)(i, j)=\sum_{m} \sum_{n} I(i+m, j+n) K(m, n)
$$
- 互相关操作的定义和神经网络中的卷积相同。
- 该操作不可交换,但其物理含义在图像处理中很重要,由于是向量直接平移后的点积计算,正好可以表示图像的相关性。
频域乘法代替空域卷积
- 频域乘法理论上可以代替空域卷积运算
- 设两时域信号$f(t), g(t)$ , 对于卷积有:
$$
f(t) * g(t)=\int_{-\infty}^{\infty} f(\tau) * g(t-\tau) d \tau
$$
- 其傅里叶变换为:
- 因此卷积可以通过下式计算:
$$
f(t) * g(t)=F^{-1}(F[f(t) * g(t)])=F^{-1}(F(w) G(w))
$$
事实上也有空域乘法相当于频域卷积的结论
频域乘法代替空域互相关
- 设两时域信号$f(t), g(t)$ , 对于互相关有:
$$
f(t) \otimes g(t)=\int_{-\infty}^{\infty} f(\tau) * g(t+\tau) d \tau
$$
- 按照同样方法推导其在频域的样子:
- 因此互相关可以通过下式计算:
- 在离散傅里叶变换中也有相同结论
快速计算空域互相关/卷积
卷积结果的傅里叶变换为信号傅里叶变换乘积这一结论为空域卷积快速计算提供了可能。- 考虑 $N\times N$ 维数据 $x$ , $M \times M$卷积核 $y$,$N \ge M$,我们需要计算二者的互相关结果
- 在空域计算时时间复杂度为 $O(N ^ 2M ^ 2)$
- 运用频域乘法计算时
- 频域乘法要求尺寸相同,因此需要将小卷积核 $Y$ pad 到和 $X$ 同样大小 ($N\times N$)
- 空域转换为频域,可以使用 FFT 加速,时间复杂度为$O(N^2logN)$,得到两组 $N\times N$ 的频域信号
- 频域数据相乘,运算复杂度为$O(N^2)$
- 因此复杂度为 $O(N^2logN)$
- 因此若 $logN < M^2$ 时会极大地减少运算量,也就是说当卷积核和数据尺寸接近时,使用频域计算卷积可以大幅加速
循环卷积
- 对于 $N\times N$ 维数据 $x,y$,当利用傅里叶变换计算互相关/卷积时,输出结果维度仍为 $N\times N$
- 那么在时域该卷积是如何 pad 的?

相位相关
- 对于两个互为循环平移的一维信号 $g_a, g_b$,维度为 $M$
$$
g_{b}(x) \stackrel{\text { def }}{=} g_{a}((x-\Delta x) \bmod M)
$$
- 信号的离散傅里叶变换将相对移位:
- 然后可以通过计算,得出相位差:
- 该频谱表示的就是时域信号中 $ \delta(x+\Delta x) $ 的傅里叶变换,因此其反变换就可以得到位移的位置了。
一维傅里叶变换的应用
计算一维周期信号的周期/频率
-
可以应用在一维周期信号的特征提取
-
给出一幅图像,我们求出图像中圆形的周期和相位

- 去均值一维信号
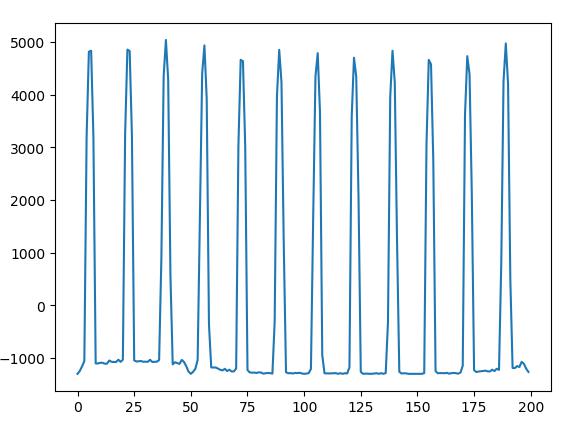
- 离散傅里叶变换,计算模长
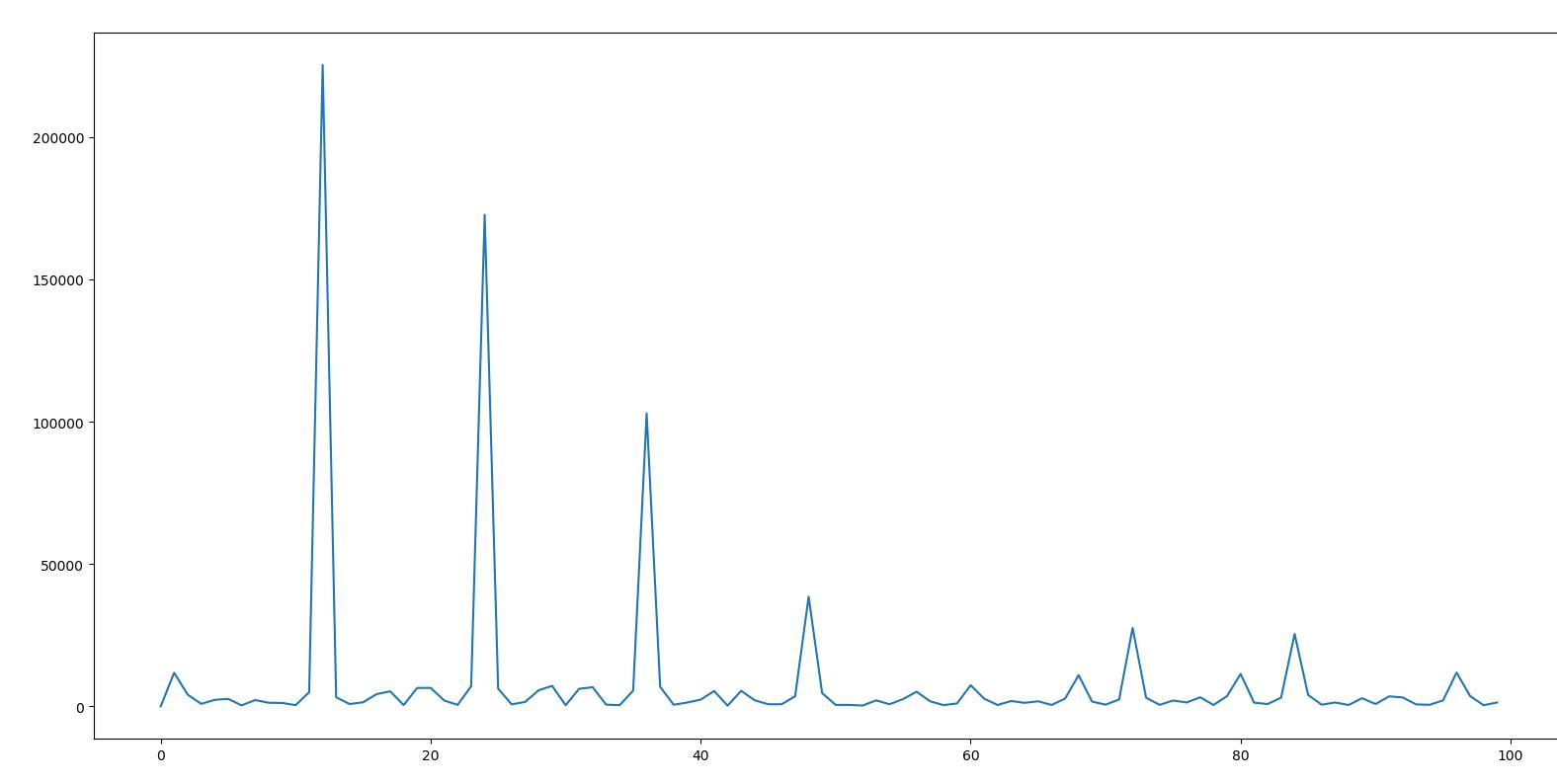
其中能量最大的就是信号的频率 12,与实际相符
- 通过计算频域复数在 12 这一点的角度,可以得到周期信号的起始相位
计算图像旋转角度
Halcon 实例:
determine grid rotation fft
- 对于图像对


- 统计二者的梯度方向累计直方图,可以发现由于旋转产生的位移偏差
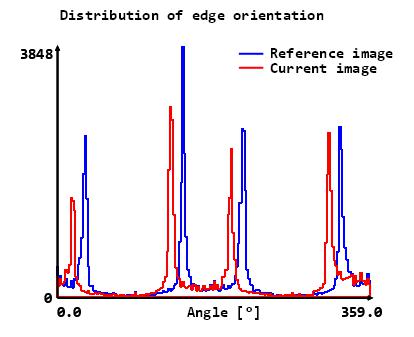
- 这样我们得到了两个循环移位的一维信号
- 此时可以用傅里叶变换求得互相关结果,选择相关性最高的点作为角度变换结果
- 也可以利用相位相关,求得信号位移在时域上的冲击相应位置,求得旋转角度
二维傅里叶变换的应用
图像压缩
- 自然图像往往有邻域强相关的特性,因此低频分量承载了更多的图像信息
- 可以运用此性质在保存图像数据时适当丢弃部分高频数据,以实现图像压缩(JPEG)

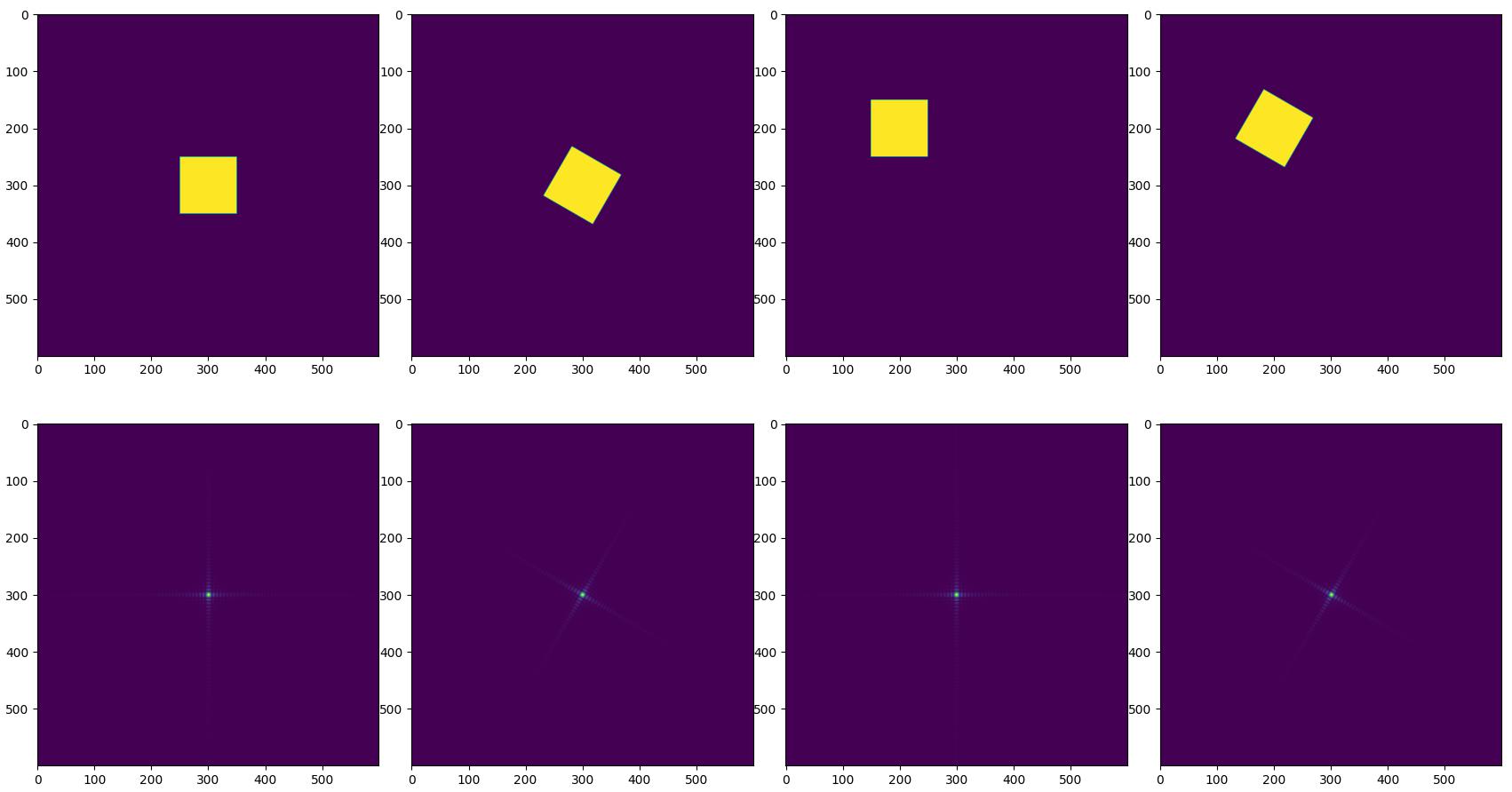
旋转和平移
- 如果旋转时域图像,由于旋转没有改变平面波的幅度相位,只是将所有的平面波都旋转了一个角度,那么频域图像也会旋转相应的角度。
- 平移时域图像,相当于周期信号没有变,仅是相位发生了变化,因此在频域中的表示是相位变化,而能量谱不变。
去掉周期性噪声
- 对于周期的背景信号,在频域空间中就会产生规律的亮点,如果将这些亮点去掉则可以起到去噪的效果


快速计算互相关
- 假设要求两幅图像 $I,T$ 的互相关结果$S$,如果二者尺寸接近,可以通过傅里叶变换的方法加速计算互相关:
相位相关计算平移参数
- 该应用常用于平移图像的平移距离搜索,通过相位相关可以计算得到平移距离:

互相关和相位相关
-
维基百科上说:
This result could have been obtained by calculating the cross correlation directly. The advantage of this method is that the discrete Fourier transform and its inverse can be performed using the fast Fourier transform, which is much faster than correlation for large images.
-
但是事实上相位相关和互相关在时域的表现差异很大,而且二者都可以通过 FFT 加速:
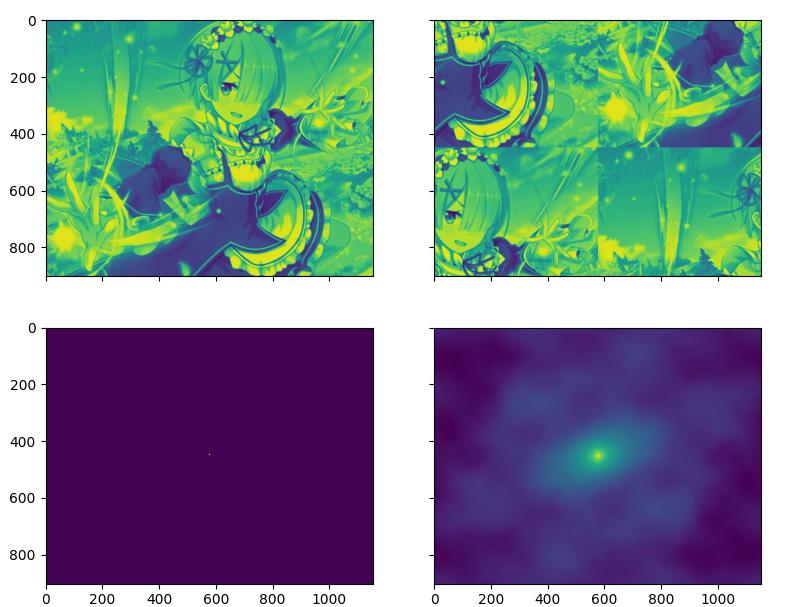
- 一个是冲击信号,一个是相关度计算的结果,在实际应用中相位相关在处理位移搜索时表现也更加鲁棒。
- 但是相位相关的问题是最大值的含义并不明确,讲道理最大值应该是 1(理想情况),但实际应用时忽大忽小,不如互相关能给出分值可解释
- 因此可以采用使用相位相关计算出的位置,定位后计算两幅图像的相关度,结合鲁棒性和可解释性给出结果。
参考资料
-
https://www.zywvvd.com/notes/study/math/fourier-transform/fourier-transform/
-
https://www.zywvvd.com/notes/study/math/fourier-transform/fourier-conv/fourier-conv/
-
https://www.zywvvd.com/notes/study/math/fourier-transform/2d-dft-corr/2d-dft/
-
https://www.zywvvd.com/notes/study/math/fourier-transform/2d-dft-corr/2d-dft-corr/
文章链接:
https://www.zywvvd.com/notes/study/math/fourier-transform/fourier-summary/fourier-summary/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付