本文最后更新于:2024年5月7日 下午
2D DFT变换在数字图像处理中有着重要应用,本文记录图像频域处理中的卷积、相关等内容。
简介
- 傅里叶变换 是一种分析信号的方法, 2D 离散傅里叶变换在数字图像处理领域可以在频域完成很多时序需要的功能。
- 常见的频域操作有卷积、互相关和相位相关操作。
卷积
- 信号处理中的卷积和神经网络中的卷积事实上并不是一个概念,在神经网络的卷积介绍中经常可以看到这样的示意图,称之为卷积,事实上是一种广义的称呼
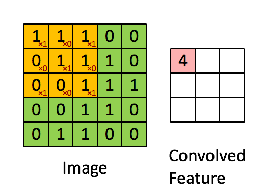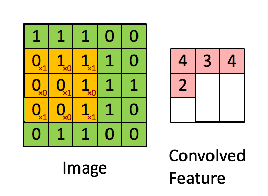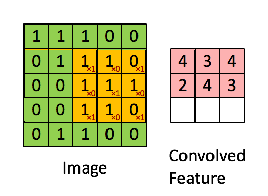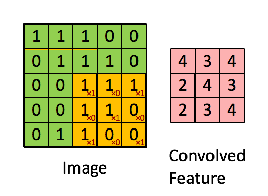
- 在信号处理中的卷积定义为:
$$
S(i, j)=(I * K)(i, j)=\sum \sum I(m, n) K(i-m, j-n)
$$
-
也就是说 $K$ 的二维信号是左右、上下翻转后再平移求向量点积的。
这点和神经网络中的卷积概念有些出入,在不同场合稍加注意就好。
-
这样设计的好处是使得卷积操作拥有了可交换性,即上式可以等价地写作:
$$
S(i, j)=(K * I)(i, j)=\sum \sum I(i-m, j-n) K(m, n)
$$
- 那么该卷积和频域信号处理有什么关系呢,事实上神奇的是时域的卷积操作相当于频域的乘法操作,一维信号我们层级有过证明,二维信号可以直接类比得到相同的结论
- 因此有:
$$
F{f(x,y)*g(x,y)}=F(x,y)G(x,y)
$$
- 那么如果我们要求两幅图像$I,T$时域卷积的结果$C$,可以通过频域乘法来做:
$$
C=IFFT(FFT(I)*FFT(T))
$$
- 其中 $FFT$ 为快速傅里叶变换,$IFFT$ 为快速傅里叶反变换
周期卷积
- 在神经网络的卷积中会有 Full, Valid, Same 等 Padding 设置,目的是在卷积过程中定义超出图像边界的计算方式。那么通过上述频域操作算出来的卷积是如何 Pad 的呢?
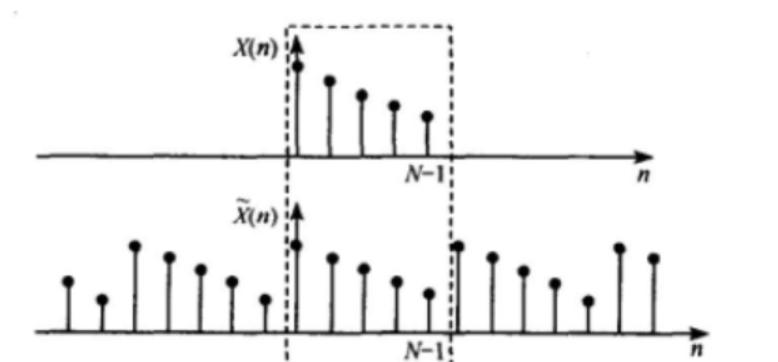
- 在 2D 傅里叶变换处理图像数据时,将图像看成了一个周期信号,将图像复制平铺铺满整个世界,计算卷积时在一张图像范围内依次卷积,也就是说左上角和右下角的值在信号计算的结果上是相邻的
互相关
- 互相关操作的定义和神经网络中的卷积相同:
$$
S(i, j)=(I * K)(i, j)=\sum_{m} \sum_{n} I(i+m, j+n) K(m, n)
$$
- 该操作不可交换,但其物理含义在图像处理中很重要,由于是向量直接平移后的点积计算,正好可以表示图像的相关性。
- 在频域中的计算推导与卷积基本相同,结果上需要改变一下相位的符号
- 假设要求两幅图像 $I,T$ 的互相关结果$S$,可以通过如下方法:
- 其中 $FFT^*(T)$ 表示 $T$ 的傅里叶变换的共轭
- 因为二者不可交换如果要计算 $T,I$ 的互相关需要反过来:
$$
S=IFFT(FFT^*(I)*FFT(T))
$$
- 此处的 Pad 处理和计算卷积时是相同的
相位相关
- 该应用常用与平移图像的平移距离搜索,通过相位相关可以计算得到平移距离:

原理
- 该方法基于傅里叶移位定理。 设图像 $g_a,g_b$ 是相互循环移位的两幅图像,尺寸为 $M\times N$:
$$
g_{b}(x, y) \stackrel{\text { def }}{=} g_{a}((x-\Delta x) \bmod M,(y-\Delta y) \bmod N)
$$
- 然后,图像的离散傅里叶变换将相对移位:
- 然后可以计算归一化互功率谱,以计算出相位差:
-
该频谱表示的就是空域信号中 $ \delta(x+\Delta x, y+\Delta y) $ 的傅里叶变换,因此其反变换就可以得到位移的位置了。
-
维基百科上说:
This result could have been obtained by calculating the cross correlation directly. The advantage of this method is that the discrete Fourier transform and its inverse can be performed using the fast Fourier transform, which is much faster than correlation for large images.
-
但是事实上相位相关和互相关在时域的表现差异很大:
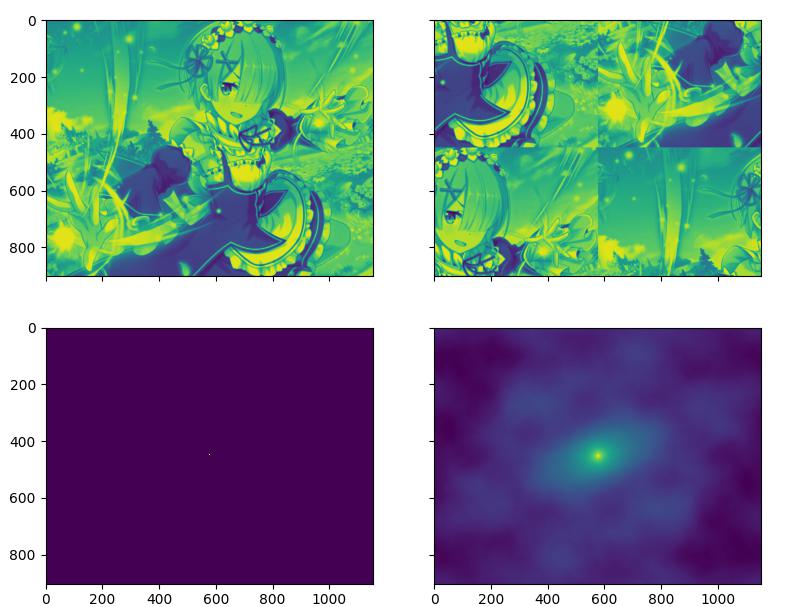
- 一个是冲击信号,一个是相关度计算的结果,分明就是不同的东西,在实际应用中相位相关在处理位移搜索时表现也更加鲁棒。
- 但是相位相关的问题是最大值的含义并不明确,讲道理最大值应该是 1(理想情况),但实际应用时忽大忽小,不如互相关能给出分值可解释
- 因此可以采用使用相位相关计算出的位置,定位后计算两幅图像的相关度,结合鲁棒性和可解释性给出结果。
参考资料
- https://en.wikipedia.org/wiki/Phase_correlation
- https://www.cnblogs.com/IllidanStormrage/p/16206837.html
- https://www.zywvvd.com/notes/study/math/fourier-transform/fourier-conv/fourier-conv/
- https://www.robots.ox.ac.uk/~az/lectures/ia/lect2.pdf
文章链接:
https://www.zywvvd.com/notes/study/math/fourier-transform/2d-dft-corr/2d-dft-corr/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付