本文最后更新于:2024年5月7日 下午
傅立叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。本文梳理基本知识。
概述
Fourier transform或Transformée de Fourier有多个中文译名,常见的有“傅里叶变换”、“付立叶变换”、“傅立叶转换”、“傅氏转换”、“傅氏变换”、等等。
- 傅立叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。所谓信号,从狭义上说可以认为是自然界中作为信息载体的各类波,一般来说简谐震动产生的正弦波是最常见的研究对象。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅立叶变换用正弦波作为信号的成分。
- 对于自然界存在的所有波,我们可以利用所谓的傅立叶级数展开法将它们分解为有限或无限个不同频率不同振幅的正弦、余弦波的集合
定义
连续傅里叶变换
- $f(t)$是$t$的周期函数,如果$t$满足狄里赫莱条件:在一个以 $2T$ 为周期内$f(X)$连续或只有有限个第一类间断点,附$f(x)$单调或可划分成有限个单调区间,则$F(x)$以$2T$为周期的傅里叶级数收敛,和函数$S(x)$也是以$2T$为周期的周期函数,且在这些间断点上,函数是有限值;在一个周期内具有有限个极值点;绝对可积。
- 则有下式成立,称为积分运算$f(t)$的傅立叶变换:
$$
F(\omega)=\mathcal{F}[f(t)]=\int_{-\infty}^{\infty} f(t) e^{-i w t} d t
$$
$ F(\omega) $ 叫做 $ {f}(\mathrm{t}) $ 的象函数, $ {f}({t}) $ 叫做$ {F}(\omega) $ 的象原函数。
$ F (\omega) $ 是 $ {f}(\mathrm{t}) $ 的象, $ \mathrm{f}({t}) $ 是$F(\omega)$原象。
- 傅里叶变换可以通过逆变换将象函数变换为象原函数
$$
f(t)=\mathcal{F}^{-1}[F(\omega)]=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{i w t} d \omega
$$
其中$F(ω)$叫做$f(t)$的象函数,$f(t)$叫做$F(\omega)$ 的象原函数。 $\mathrm{F}(\omega)$ 是 $f(\mathrm{t})$ 的象。 ${f}({t})$ 是 $\mathrm{F}(\omega)$ 原象。
- 傅立叶逆变换证明:
$$
\begin{array}{c}
\int_{-\infty}^{\infty} F(\omega) e^{i w t} d \omega
&=&\int_{-\infty}{\infty}\left[\int_{-\infty}{\infty} f(x) e^{-j w x} d x\right] e^{j w t} d w\
&=& \int_{-\infty}{\infty}\left[\int_{-\infty}{\infty} e^{-j w(x-t)} d w\right] f(x) d x \
&=& \int_{-\infty}^{\infty}[2 \pi \delta(x-t)] f(x) d x \
&=& 2 \pi f(t)
\end{array}
$$
离散傅里叶变换
傅里叶级数适用于周期时间连续且无限长度的信号处理。但是我们需要对待处理信号进行采样,并且信号常常并非是周期的,同时采样时间也不可能是无穷长,这就意味着我们需要一个能够处理非周期离散时间信号的变换公式。
- 设 $x(n)$ 是一个长度为 $M$ 的有限长序列,则定义 $x(n)$ 的 $N$ 点离散傅里叶变换为
$$
X(k)=\operatorname{DFT}[x(n)]=\sum_{n=0}^{N-1} x(n) W_{N}^{k n} \quad k=0,1, \cdots, N-1
$$
- $X(k)$ 的离散傅里叶逆变换(Inverse Discrete Fourier Transform, IDFT)为
$$
x(n)=\operatorname{IDFT}[X(k)]=\frac{1}{N} \sum_{k=0}^{N-1} X(k) W_{N}^{-k n} \quad n=0,1, \cdots, N-1
$$
式中, $W_{N}=\mathrm{e}^{-j\frac{2\pi}{N}}, N$ 称为 $\mathrm{DFT}$ 变换区间长度, $(N \geqslant M)$ 通常称上述两式为离散傅里叶变换对。
为了叙述简洁,常常用 ${DFT[x(n)]} _ { N}$ 和 $IDFT[X(k)]_{N}$ 分别表示 $N$ 点离散傅里叶变换和 $N$ 点离散傅里叶逆变换。
相关概念
虽然讲了定义,相信没人能直接看懂,了解一些相关概念明白一下傅里叶变换是在干嘛。
时域
是描述数学函数或物理信号对时间的关系。例如一个信号的时域波形可以表达信号随着时间的变化。是真实世界,是惟一实际存在的域。因为我们的经历都是在时域中发展和验证的,已经习惯于事件按时间的先后顺序地发生。
频域
频域(frequency domain)是描述信号在频率方面特性时用到的一种坐标系。在电子学,控制系统工程和统计学中,频域图显示了在一个频率范围内每个给定频带内的信号量。频域,尤其在射频和通信系统中运用较多,在高速数字应用中也会遇到频域。频域最重要的性质是:它不是真实的,而是一个数学构造。时域是惟一客观存在的域,而频域是一个遵循特定规则的数学范畴,频域也被一些学者称为上帝视角。
时域频域的关系
时域分析与频域分析是对模拟信号的两个观察面。时域分析是以时间轴为坐标表示动态信号的关系;频域分析是把信号变为以频率轴为坐标表示出来。一般来说,时域的表示较为形象与直观,频域分析则更为简练,剖析问题更为深刻和方便。信号分析的趋势是从时域向频域发展。然而,它们是互相联系,缺一不可,相辅相成的。
- 傅里叶正变换和反变换,就是将信号在二者之间变换。
- 不同频率的正弦波相互正交,构成了频域空间上的基
- 傅里叶正变换就是当前的信号与所有频率不同相位的正弦信号计算点积,得到各个频率波上的分量,叠加构成当前的时域信号
实际应用
- 给出一幅图像,我们求出图像中圆形的周期和相位

- 将图像极坐标变换
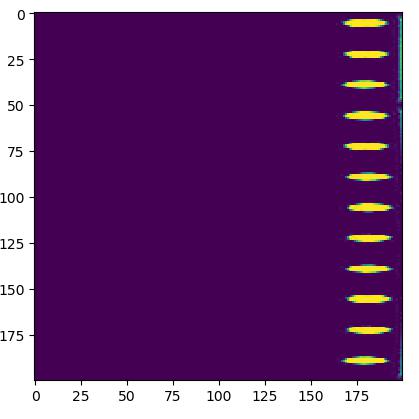
- 叠加减去均值得到时域信号:
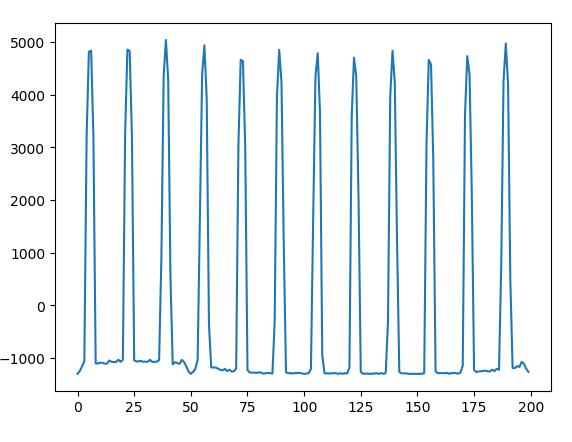
- 离散傅里叶变换,计算模长
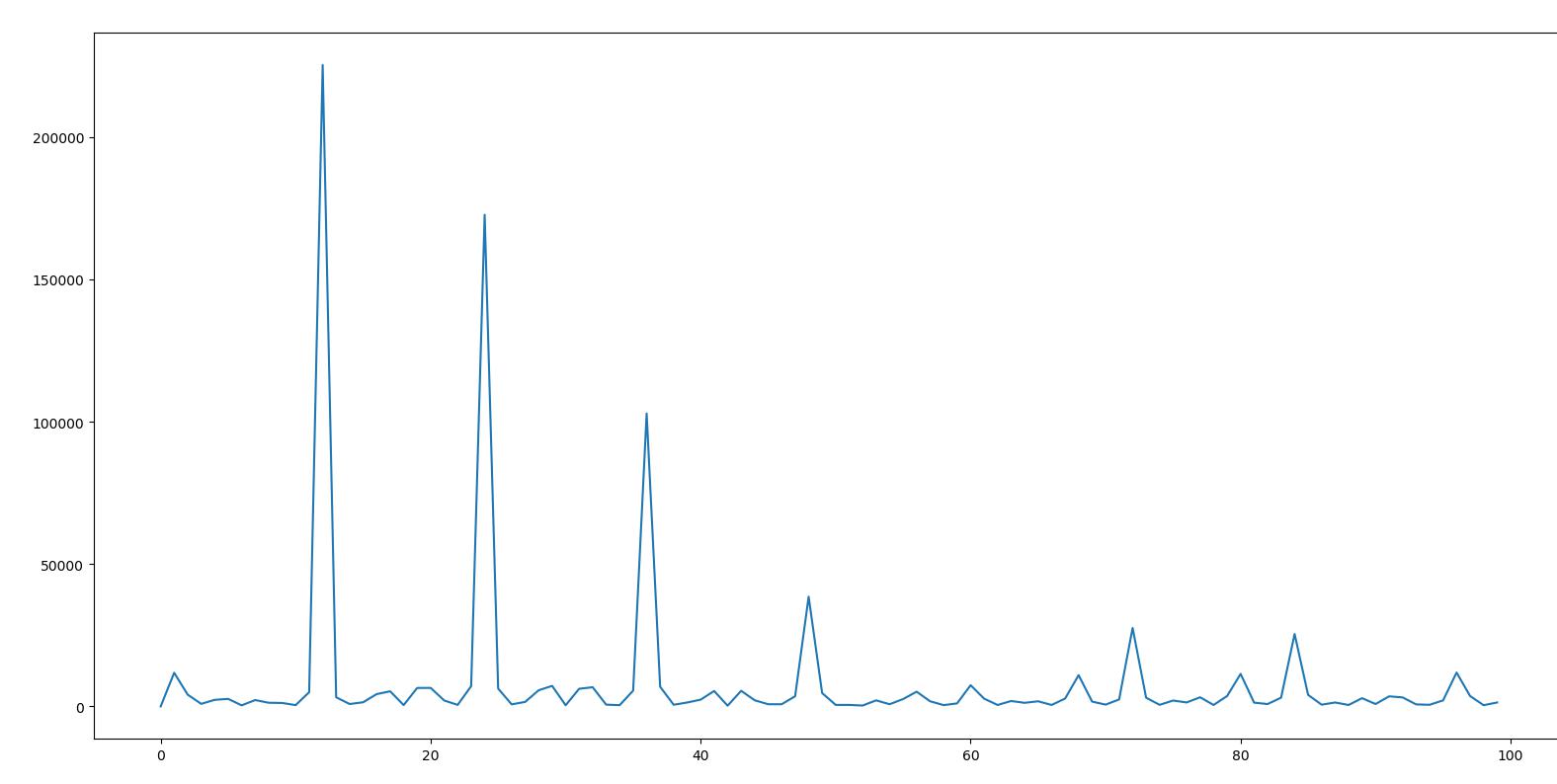
-
其中能量最大的就是信号的周期 12,与实际相符
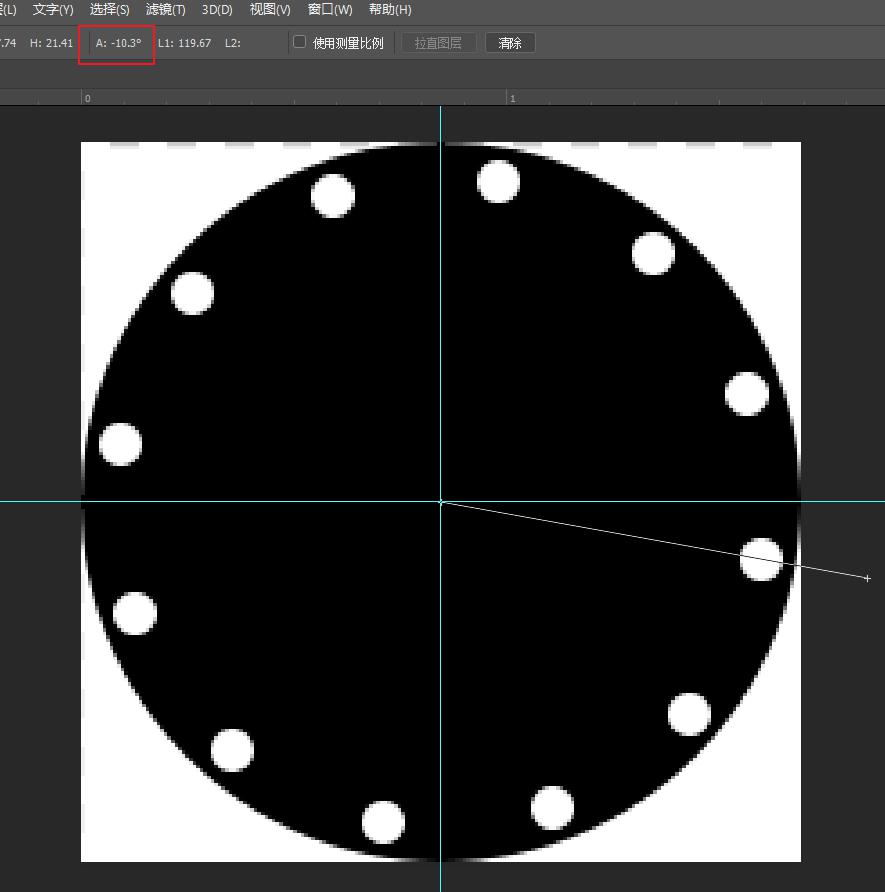
-
计算频率为12的相位,得到 -10.279644688897708,与实际相符
参考代码
1 | |
参考资料
- https://baike.baidu.com/item/傅里叶变换/7119029?fr=aladdin
- https://www.cnblogs.com/amanlikethis/p/3505248.html
- https://www.zhihu.com/question/21040374
- https://baike.baidu.com/item/时域频域/9399325?fr=aladdin
- https://zhuanlan.zhihu.com/p/77345128
- https://zhuanlan.zhihu.com/p/426411907
文章链接:
https://www.zywvvd.com/notes/study/math/fourier-transform/fourier-transform/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付