2D 离散傅里叶变换

本文最后更新于：2024年5月7日下午

2D DFT变换在数字图像处理中有着重要应用，本文记录相关概念和简单应用。

简介

傅里叶变换是一种分析信号的方法，将时域信号在频域的基中重新表示，而在频域中可能会有时域难以实现的操作效果。
对于数字图像处理来说，离散的 2D 傅里叶变换是更加实用的理论，根据傅里叶变换的性质我们可以使用傅里叶变换进行时域的卷积、相关等操作

2D 傅里叶变换

1D 傅里叶变换是将时域信号用频域空间的基——不同频率的正弦、余弦波表示后的结果，那么 2D 傅里叶变换本质是什么呢

一维傅里叶变换

回顾一维傅里叶变换：

$$
F(w)=\int_{-\infty}^{+\infty} f(x) e^{-j w x} d x
$$

通俗来讲，一维傅里叶变换是将一个一维的信号分解成若干个复指数波 $ e^{j w x} $ 。而由于 $ e^{j w x}=\cos (w x)+i \sin (w x) $ ，所以可以将每一个复指数波 $ e^{j w x} $ 都视为是 $余弦波 +\mathrm{j} {\times} 正弦波$ 的组合。

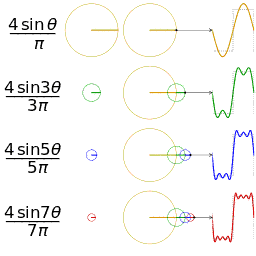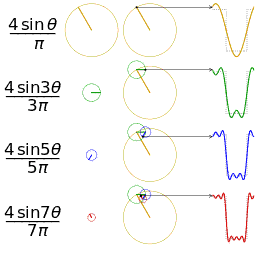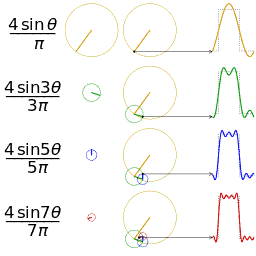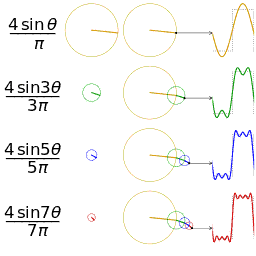
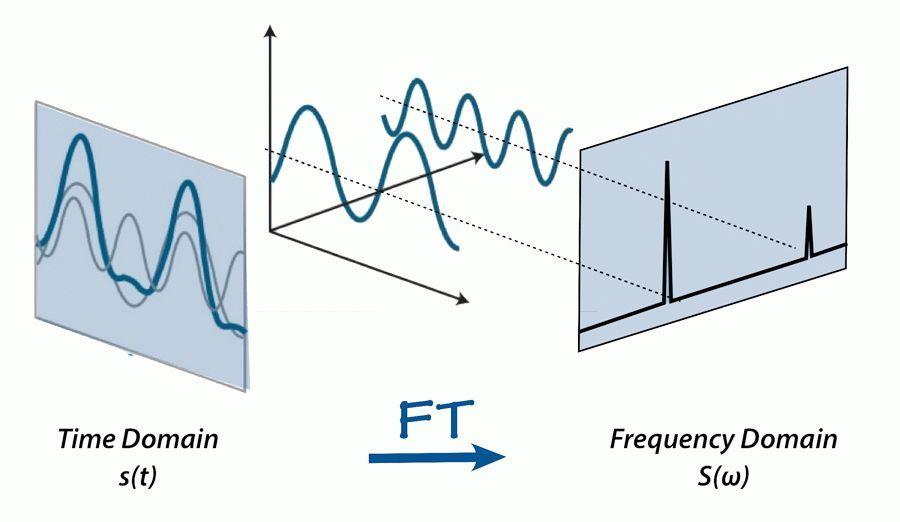
对于一个正弦波而言，需要三个参数来确定它：频率 $w$ ,幅度 $A$ ，相位 $φ$ 。因此在频域中，一维坐标代表频率，而每个坐标对应的函数值也就是 $F(w)$ 是一个复数，其中它的幅度 $|F(w)|$ 就是这个频率正弦波的幅度 $A$ ，相位 $∠F(w)$ 就是 $φ$ 。下图右侧展现的只是幅度图，在信号处理中用到更多的也是幅度图。

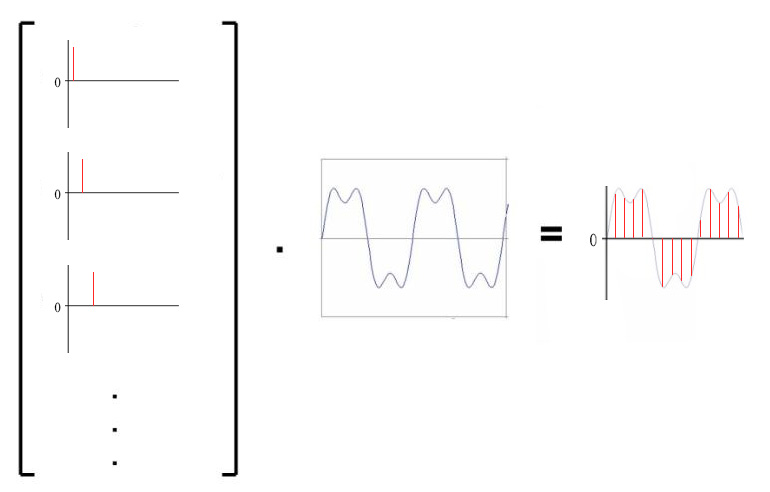
一维傅里叶变换就是一个基变换，在时域中，基是一族冲激信号 $ {\delta(x-n)} $

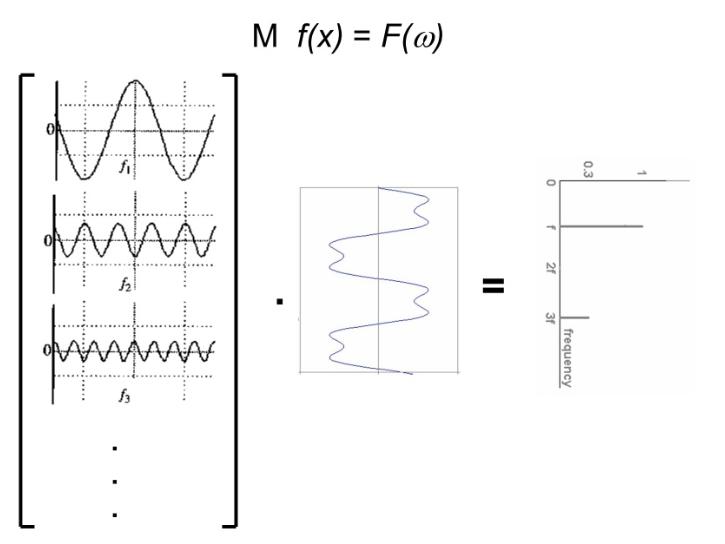
在频域中; 基是 $ \left\{e^{j w x}\right\} $ ，而且这组基是正交基。

类比：从一维到二维

一维信号是一个序列，傅里叶变换将其分解成若干个一维的简单函数之和。

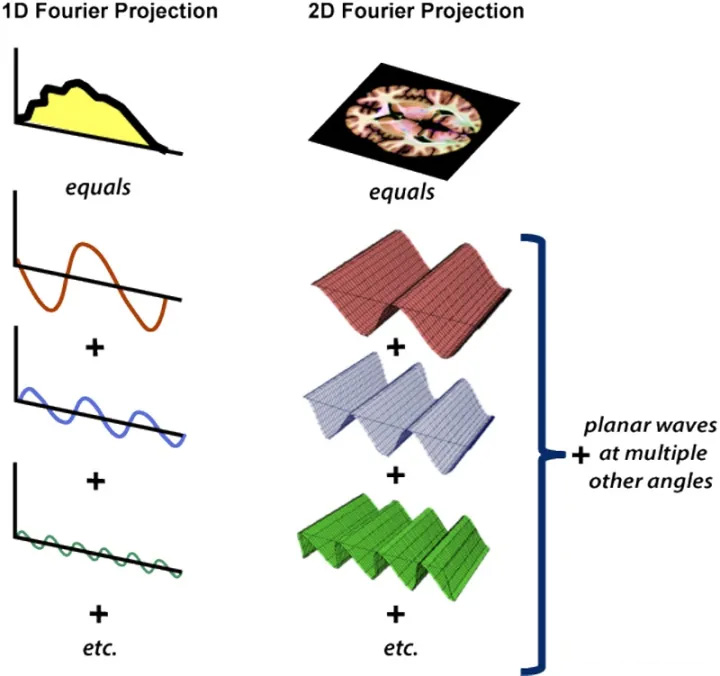
二维的信号可以说是一个图像，类比一维，那二维傅里叶变换是不是将一个图像分解成若干个简单的图像呢？

事实上二维傅里叶变换将一个图像分解成若干个复平面波 $ e^{j 2 \pi(u x+v y)} $ 之和。

二维连续傅里叶变换的公式:

$$
F(u, v)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) e^{-j 2 \pi(u x+v y)} d x d y
$$

通过公式，我们可以计算出，每个平面波在图像中成分是多少。从公式也可以看到，二维傅里叶变换就是将图像与每个不同频率的不同方向的复平面波做内积，也就是一个求在基 $ \left\{e^{-j 2 \pi(u x+v y)}\right\} $ 上的投影的过程。

应该知道 $ \frac{\vec{a} \cdot \vec{b}}{|\vec{a}|} $ 是b在a上的投影，只不过这里的|a|的值被设为 1 , 所以只有内积。

二维频域 K-SPACE （K空间）

对于正弦平面波，可以这样理解，在一个方向上存在一个正弦函数，在法线方向上将其拉伸。前面说过三个参数可以确定一个一维的正弦波。哪几个参数可以确定一个二维的正弦平面波呢? 答案是四个，其中三个和一维的情况一样 (频率 $ w $, 幅度 $ A $ ，相位 $ \varphi $ )，但是具有相同这些参数的平面波却可以有不同的方向 $ \vec{n} $ 。如下图所示:

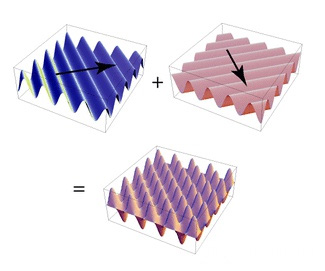
类比一维中，幅度和相位可以用一个复数表示，它可以作为我们存储的内容。但是还有两个：一个频率一个方向。这时想到向量是有方向的，也是有长度的。所以我们用一个二维的矩阵的来保存分解之后得到的信息。这个矩阵就是K空间。（一般用k来表示空间频率)
就是说一个二维矩阵点 $ (u, v) $ 代表这个平面波的法向量 $ \vec{n} $ ，这个向量的模$ \sqrt{u^{2}+v{2}} $ 代表这个平面波的频率 $ w $ ，这个点里面保存的内容复数就是此平面波的幅度和相位。下面这个图很好的体现了这一点:

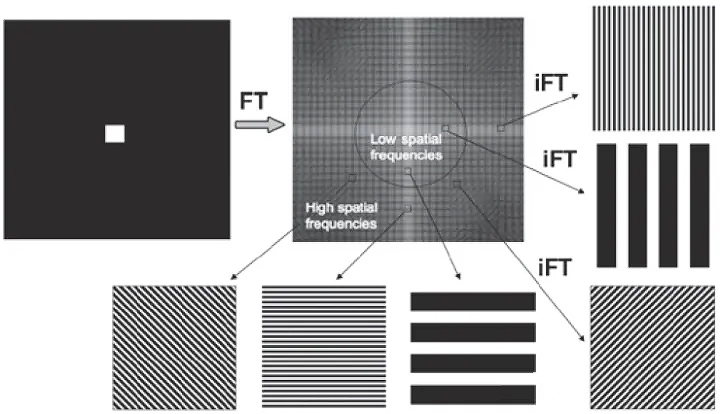
也因比K空间的中心对于低频，周围对于高频。如下图，K空间中只有(0,0)处有值，也就是信号都是直流即不存在变化，所以实空间就是一张白纸。

中心低频贡献了图像的主体，周围高频提供图像的细节和边缘。

k空间的每一个位置存储诸的数代表了所在位置复平面波在图像中占多少成分，我们就河以用每个系数 $\times$ 所代表的平面波相加得到原来的图像。所以k空间和对应图像储存的信息含量是一样的，只不过表现形式不同，或者说基不同。

旋转和平移

如果旋转时域图像，由于旋转没有改变平面波的幅度相位，只是将所有的平面波都旋转了一个角度，那么频域图像也会旋转相应的角度。
平移时域图像，相当于周期信号没有变，仅是相位发生了变化，因此在频域中的表示是相位变化，而能量谱不变。

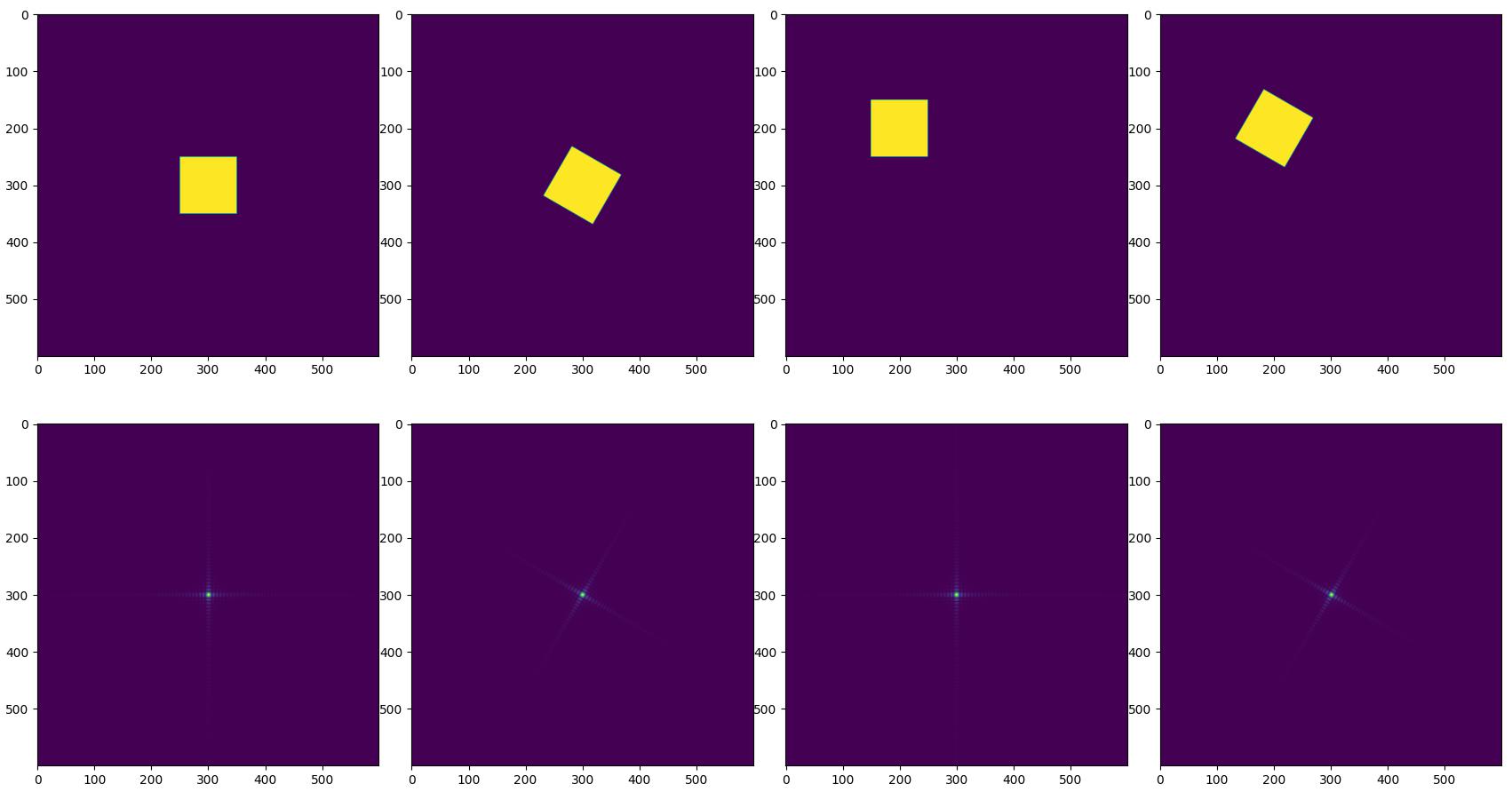
生成代码

import numpy as np
import mtutils as mt


if __name__ == '__main__':

    golden_img = np.zeros([600, 600])
    golden_img[250:350, 250:350] = 255

    H, W = golden_img.shape[:2]

    gloden_fft = np.fft.fft2(golden_img)
    ori_fft_res = np.abs(np.fft.fftshift(gloden_fft))

    rotate_img = mt.img_rotate(golden_img, 30)
    rotate_fft = np.fft.fft2(rotate_img)
    rotate_fft_res = np.abs(np.fft.fftshift(rotate_fft))

    roi = [100, 100, W+100, H+100]
    moved_img = mt.crop_data_around_boxes(golden_img, roi)
    moved_fft = np.fft.fft2(moved_img)
    moved_fft_res = np.abs(np.fft.fftshift(moved_fft))

    roi = [100, 100, W+100, H+100]
    moved_rotated_img = mt.crop_data_around_boxes(rotate_img, roi)
    moved_rotated_fft = np.fft.fft2(moved_rotated_img)
    moved_rotated_fft_res = np.abs(np.fft.fftshift(moved_rotated_fft))

    mt.PIS(golden_img, rotate_img, moved_img, moved_rotated_img, ori_fft_res, rotate_fft_res, moved_fft_res, moved_rotated_fft_res, row_num=2)