斯特林公式(Stirling's approximation)

本文最后更新于：2024年5月7日下午

斯特林公式（Stirling’s approximation）是一条用来取n的阶乘的近似值的数学公式。

简介

斯特林公式（Stirling’s approximation）是一条用来取 $n$ 的阶乘的近似值的数学公式。一般来说，阶乘的计算复杂度为线性。当要为某些极大的 $n$ 求阶乘时，常见的方法复杂度不可接受。斯特林公式能够将求解阶乘的复杂度降低到对数级。而且，即使在 $n$ 很小的时候，斯特林公式的取值已经十分准确。

公式

$$
n ! \approx \sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}
$$

极限形式
$$
\lim _{n \rightarrow+\infty} \frac{n !}{\sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}}=1
$$

证明

对 $n!$ 取对数
$$
\ln (n !)=\ln 1+\ln 2+\ln 3+\ldots+\ln n
$$
上式同时减去 $\frac{\ln ⁡n}{2}$

$$ \begin{array}{c} \ln (n !)-\frac{\ln n}{2} &=\ln 1+\ln 2+\ln 3+\ldots+\ln n-\frac{\ln n}{2}\\ &= \frac{\ln 1+\ln 2}{2}+\frac{\ln 2+\ln 3}{2}+\ldots+\frac{\ln (n-1)+\ln n}{2} \end{array} $$

之所以构造这个形式是为了构造积分梯形法则，考虑函数 $f(x)=\ln x$ ，在其中做梯形面积累加：

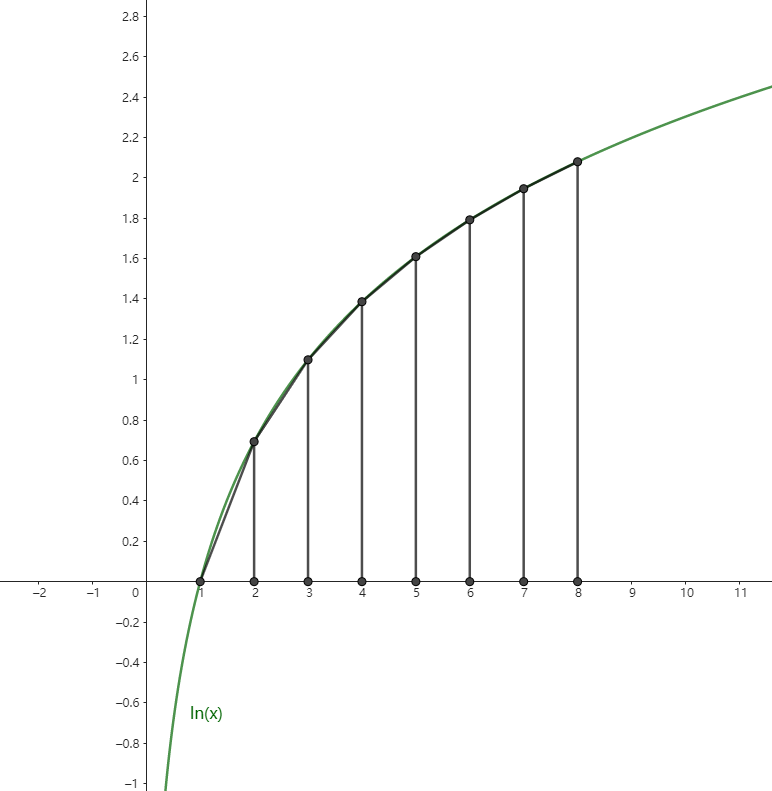
令梯形面积和为 $ G(n)=\ln (n !)-\frac{\ln n}{2} $

令积分面积和为:

$$ \begin{array}{l} H(n)&=\int_{1}^{n} \ln x d x \\ &=\int_1^n d(x\ln x-x)\\ &=x\ln x-x|^n_1\\ &=n\ln n-n+1 \end{array} $$

运用积分梯形法则，由于有 $n-1$ 个梯形，二者误差 $E(n)$ 为
$$
E(n)=G(n)-H(n)=-\sum_{i=2}^{n} \frac{f^{\prime \prime}(\xi_i)}{12}
$$
因为 $ f^{\prime \prime}(\xi_i)$ 描述的是第 $i$ 个小梯形内部的某个取值

又 $f’'(\xi)=-\frac{1}{\xi^2}$

因此 $ f''(\xi_i)\in\left[-\frac{1}{(i-1)^{2}},-\frac{1}{i^{2}}\right] $

对于任意小的正数 $\epsilon $ ，总能找到正整数 $M$，记 $S(M) = \sum_{i=2}^{M} \frac{f^{\prime \prime}(\xi_i)}{12}$ ，$L(M) = \sum_{i=M}^{+\infty} \frac{f^{\prime \prime}(\xi_i)}{12}$，有：

$$ L(M) = \sum_{i=M}^{+\infty} \frac{f^{\prime \prime}(\xi_i)}{12} \leq \sum_{i=M}^{+\infty}\frac{\sup \left\{\left|f^{\prime \prime}(\xi_i)\right|\right\}}{12}=\sum_{i=M}^{+\infty}\frac{1}{12(M-1)^2}<\epsilon $$

因此对于给定的任意一组$M$和$\epsilon$ :
$$
E(n)=S(M)+L(M)<S(M) +\epsilon
$$
因此 $E(n)$ 有上界。

并且 $E(n)$ 作为累积误差单调递增，因此 $E(n)$ 会收敛于某个常数 $c$
$$
\lim _{n \rightarrow \infty} E(n)=c
$$
于是，在 ${n \rightarrow \infty} $ 时：

$$ \begin{array}{l} G(n)-H(n)&=c\\ \ln (n!)-\frac{\ln n}{2}-n\ln n +n -1&=c\\ \ln (n !)-\frac{\ln n}{2}&=(n \ln n-n)+c \\ \frac{n !}{\sqrt{n}}&=\left(\frac{n}{e}\right)^{n} e^{c} \\ n !&=\sqrt{n}\left(\frac{n}{e}\right)^{n} e^{c} \end{array} $$

由 Wallis 公式

$$
\sqrt{\pi}=\lim _{n \rightarrow \infty} \frac{(2 n) ! !}{\sqrt{n}(2 n-1) ! !}
$$
即

$$ \begin{aligned} \sqrt{\pi} & =\lim _{n \rightarrow \infty} \frac{2^{n} n !(2 n-2) ! !}{\sqrt{n}(2 n-1) !}\\ &=\lim _{n \rightarrow \infty} \frac{2^{n} n ! 2^{n-1}(n-1) !}{\sqrt{n}(2 n-1) !} \\ & \stackrel{\frac{n !}{\sqrt{n}}=\left(\frac{n}{e}\right)^{n} e^{c}}{=}\lim _{n \rightarrow \infty} \frac{2^{2 n-1}(n-1) !\left(\frac{n}{e}\right)^{n} e^{c}}{(2 n-1) !} \\ & \stackrel{n !=\sqrt{n}\left(\frac{n}{e}\right)^{n} e^{c}}{=} \lim _{n \rightarrow \infty} \frac{2^{2 n-1} \sqrt{n-1}\left(\frac{n-1}{e}\right)^{n-1} e^{c}\left(\frac{n}{e}\right)^{n} e^{c}}{\sqrt{2 n-1}\left(\frac{2 n-1}{e}\right)^{2 n-1} e^{c}} \\ & =\lim _{n \rightarrow \infty} \frac{2^{2 n-1}e^{c} \sqrt{n-1} \left(\frac{n-1}{e}\right)^{n-1} \left(\frac{n}{e}\right)^{n}}{\sqrt{2 n-1}\left(\frac{2 n-1}{ e}\right)^{2n-1}} \\ &=\lim_{n \rightarrow \infty} e^{c}\frac{\sqrt{n-1}}{\sqrt{2n-1}}\frac{\frac{(2n-2)^{n-1}(2n)^n}{e^{2n-1}}}{\frac{(2n-1)^{2n-1}}{e^{2n-1}}} \\ & =\lim _{n \rightarrow \infty} \frac{e^{c}}{\sqrt{2}} \end{aligned} $$

因此
$$
\lim _{n \rightarrow \infty} e^{c}=\sqrt{2 \pi}
$$
得斯特林公式， $ n \rightarrow \infty $ 时
$$
n !=\sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}
$$

斯特林公式的精度

斯特林公式在 $n$ 不大的时候已经很精准了，我们尝试计算其精度

上界

根据上文的梯形法则计算原理，结合$\ln x$ 函数二阶导为负数的事实，可以知道 $[1,n]$ 内梯形面积和永远小于原始函数积分面积，因此有：

$$ \begin{array}{l} G(n) < H(n) \\ \ln (n !)- \frac{\ln n}{2} < n\ln n-n+1\\ \ln (n !) < (n+\frac{1}{2}) \ln n -n +1 \end{array} $$

下界

考虑传统的积分放缩法

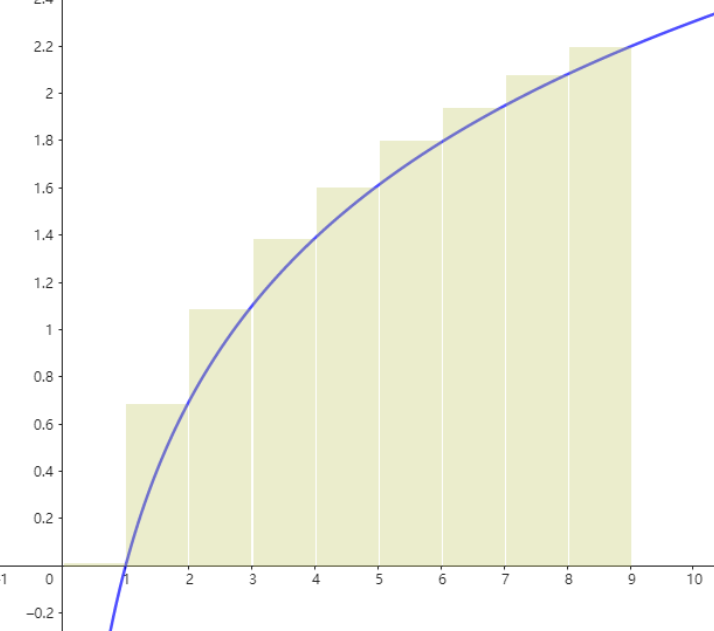
可以得到：
$$
\ln (n !) \ge \int_1^n \ln xdx
$$
但是由这个不等式推出的结论不够紧致，为了得到更紧致的估计，我们将所有的矩形向右平移 0.5

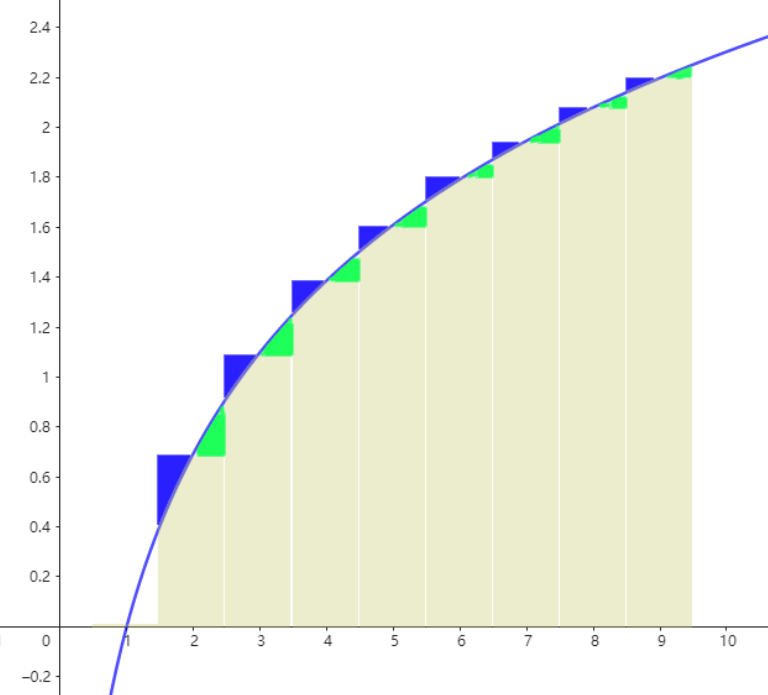
这样对于每个矩形区域，矩形面积和在该矩形横坐标覆盖范围内的积分的大小关系取决于图中同一个矩形内蓝色和绿色面积的大小关系。

由于 $\ln x$ 的二阶导为负数，以矩形中点为界，向左、向右的两个面积区域中，距离中点距离相等的两个点来说，蓝色区域内的高度会大于绿色区域内的高度。

因此对于每个矩形，形成的蓝色面积要大于绿色面积，因此矩形面积大于积分面积，有：
$$
\ln (n !) \ge \int_{1.5}^{n+0.5} \ln xdx
$$
根据 $H(n)$ 的计算方式可以推得：

$$ \begin{array}{l} \int_{1.5}^{n+0.5} \ln xdx&=x\ln x-x|^{n+0.5}_{1.5}\\ &=(n+\frac{1}{2})\ln (n+\frac{1}{2}) - n-\frac{1}{2}-\frac{3}{2}\ln\frac{3}{2}+\frac{3}{2}\\ &=(n+\frac{1}{2})\ln (n+\frac{1}{2})-n+1-\frac{3}{2}\ln\frac{3}{2} \end{array} $$

因此
$$
\ln (n !) \ge (n+\frac{1}{2})\ln (n+\frac{1}{2})-n+1-\frac{3}{2}\ln\frac{3}{2}>(n+\frac{1}{2})\ln n-n+1-\frac{3}{2}\ln\frac{3}{2}
$$
综上可得
$$
(n+\frac{1}{2})\ln n-n+1-\frac{3}{2}\ln\frac{3}{2}<\ln (n !) < (n+\frac{1}{2})\ln n -n +1
$$
而 $\frac{3}{2}\ln\frac{3}{2} \approx 0.61$，因此该公式会将 $n!$ 限制在很小的区间范围内，得到很高的计算精度。