本文最后更新于:2023年12月5日 下午
放缩法的基本原理是通过找到一个上界和一个下界来限定积分的范围,本文记录相关内容。
描述 一
对于函数的某段单调区间上的积分计算,用分段的矩形面积近似积分结果,不同划分矩形的方式得到的结果与积分真实结果存在固定的大小关系。
以递增函数为例。
RHS
从 $f(x)$ 向左绘制矩形区域
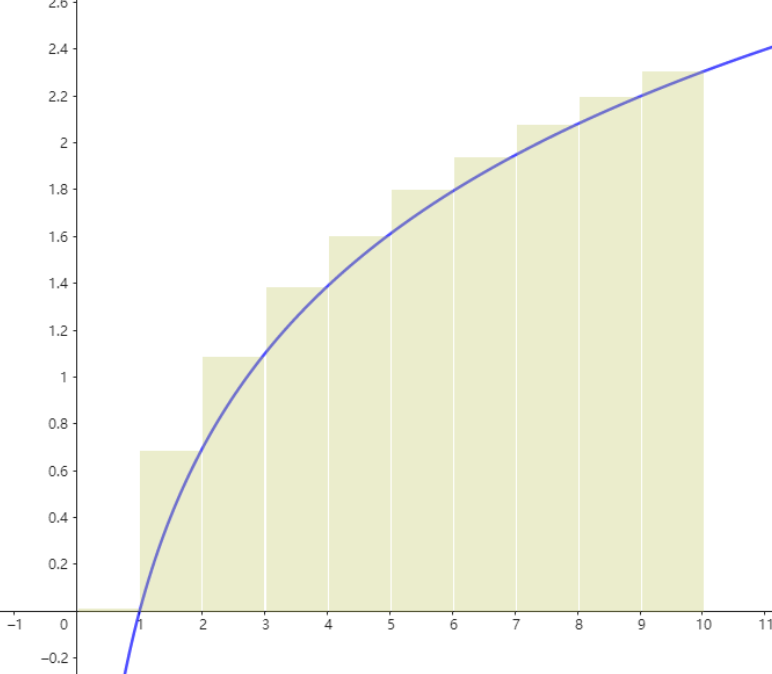
如此划分的矩形面积和大于积分结果:
$$
\int_1^{n}f(x)dx \le \sum _{i=2}^nf(i)
$$
LHS
从 $f(x)$ 向右绘制矩形区域
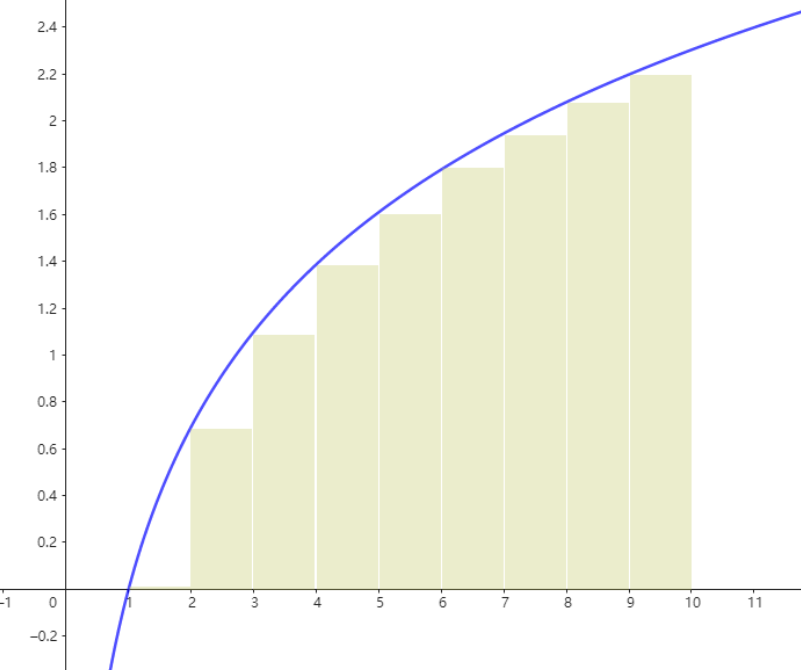
如此划分的矩形面积小于积分结果
$$
\int_1^{n}f(x)dx \ge \sum _{i=1}^{n-1}f(i)
$$
得到在这种情况下:
$$
\sum _{i=1}^{n-1}f(i) \le \int_1^{n}f(x)dx \le\sum _{i=2}^nf(i)
$$
描述 二
在函数的单调区区间上,函数值与矩形积分之间存在固定的大小关系
以递减函数为例。
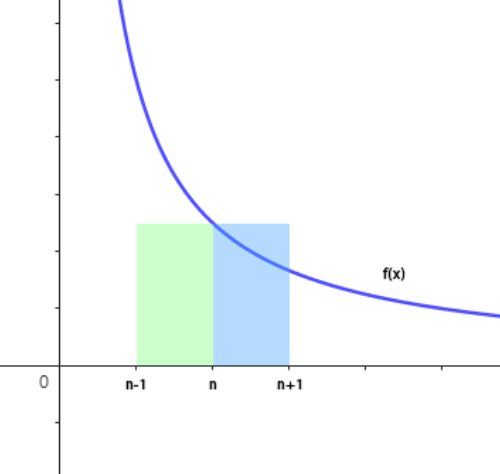
LHS
在 $[n,n+1]$ 上的积分小于等于矩形面积:
$$
\int_n^{n+1}f(x) \le f(n)
$$
RHS
在 $[n-1, n]$ 上的积分大于等于矩形面积:
$$
f(n) \le \int_{n-1}^{n}f(x)
$$
因此有:
$$
\int_n^{n+1}f(x) \le f(n)\le \int_{n-1}^{n}f(x)
$$
参考资料
文章链接:
https://www.zywvvd.com/notes/study/math/integral-scaling/integral-scaling/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付