本文最后更新于:2024年5月7日 下午
梯形法则是采用梯形来估计曲线下方面积,这等同将被积函数近似为直线函数,被积的部分近似为梯形,本文记录相关内容。
简介
梯形法则是采用梯形来估计曲线下方面积,这等同将被积函数近似为直线函数,被积的部分近似为梯形,要求得较准确的数值,可以将要求积的区间分成多个小区间。
一阶牛顿-柯特斯闭型积分公式称为梯形法则(trapezoidal rule),下面先介绍牛顿-柯特斯公式。
牛顿-柯特斯公式
牛顿-柯特斯公式(Newton-Cotes formulas)是一种常用的数值积分公式。它的基本策略是用另一个易于积分的近似函数替换被积函数或表格型数据,即
$$
I=\int_{a}^{b} f(x) d x \cong \int_{a}^{b} f_{n}(x) d x
$$
其中,$ f_{n}(x) $ 是具有如下形式的多项式
$$
f_{n}(x)=a_{0}+a_{1} x+\ldots+a_{n-1} x^{n-1}+a_{n} x^{n}
$$
$n$ 为多项式的系数。
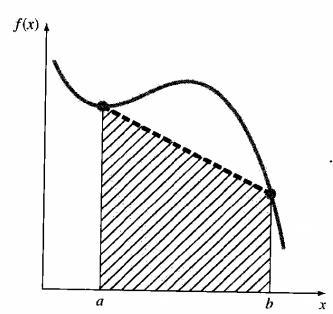
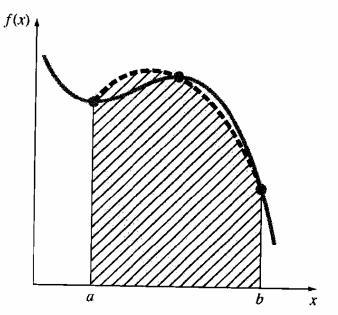
也可以将整个积分区间分成若干个等距的子区间,每个子区间上使用分段多项式来逼近函数或等距间隔的数据。
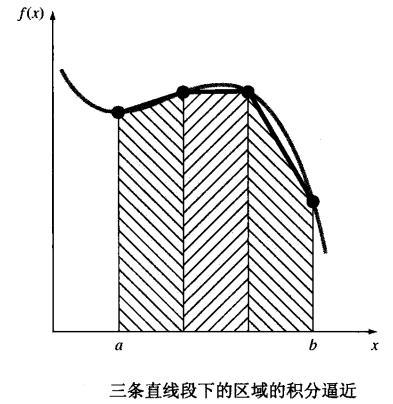
牛顿-柯特斯公式分为闭型(closed forms)和开型(open forms)两类。在积分过程中,如果积分区间两端的数据点是已知的,则称为闭型积分,反之,若积分区间超出了数据范围,则称为开型积分 。这里主要介绍闭型积分公式。
梯形法则
一阶牛顿-柯特斯闭型积分公式称为梯形法则(trapezoidal rule),即使用一次多项式
$$
I=\int_{a}^{b} f(x) d x \cong \int_{a}^{b} f_{1}(x) d x
$$
直线可以表示为
$$
f_{1}(x)=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)
$$
用这条直线下的面积作为积分 $ \int_{a}^{b} f(x) d x $ 的估计值
$$
I=\int_{a}^{b}\left[f(a)+\frac{f(b)-f(a)}{b-a}(x-a)\right] d x
$$
积分的结果为
$$
I=(b-a) \frac{f(a)-f(b)}{2}
$$
此公式称为梯形法则。
从几何上看,梯形法则相当于用连接$f(a)$和$f(b)$的直线与坐标轴所围梯形的面积来逼近积分。
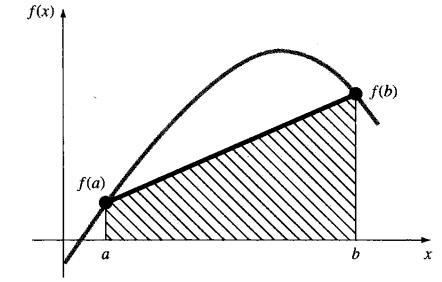
梯形法则的误差
很明显,在使用直线段下的积分逼近曲线积分的过程中,不可避免地会引入误差 。 对于单应用型梯形法则,对于单应用型梯形法则,近似局部截断误差为
$$
E_{t}=-\frac{1}{12} f^{\prime \prime}(\xi)(b-a)^{3}
$$
其中 $ (a \leq \xi \leq b) $,即
$$
\int_{a}^{b} f(x) \mathrm{d} x-\frac{b-a}{2}(f(a)+f(b))=-\frac{(b-a)^{3}}{12} f^{\prime \prime}(\xi)(a \leq \xi \leq b)
$$
引理证明
首先我们先证明一个引理 :
- 对 $ \forall x \in[a, b] , \exists \xi=\xi(x) \in(a, b) $ 使得
$$
f(x)-\frac{x-b}{a-b} f(a)-\frac{x-a}{b-a} f(b)=\frac{f^{\prime \prime}(\xi)}{2}(x-a)(x-b)
$$
也就是说,左边这串其实是 $f(x)$ 与其一次多项式插值函数 $p(x)$ 的差,$p(x)$ 我们记为 $ \frac{x-b}{a-b} f(a)+\frac{x-a}{b-a} f(b) $,需要证明的式子变为:
$$
f(x)-p(x)=\frac{f^{\prime \prime}(\xi)}{2}(x-a)(x-b)
$$
可以用数学分析中处理中值问题常用的技巧k值法来解决这个问题。
假设 $k$ 满足
$$
f(x)-p(x)=\frac{k}{2}(x-a)(x-b)
$$
令
$$
F(t)=f(t)-p(t)-\frac{k}{2}(t-a)(t-b)
$$
那么 $ F(a)=F(b)=F(x)=0 $,$ F’(a)=F’(b)$
应用罗尔定理
$$
\exists \xi \in(a, b) \rightarrow F^{\prime \prime}(\xi)=f^{\prime \prime}(\xi)-k=0
$$
引理得证。
证明
对 $f(x)-\frac{x-b}{a-b} f(a)-\frac{x-a}{b-a} f(b)=\frac{f^{\prime \prime}(\xi)}{2}(x-a)(x-b)$ 两边在 $a$ 到 $b$ 上积分:
$$
\int_{a}^{b} f(x) \mathrm{d} x-\frac{b-a}{2}(f(a)+f(b))=\int_{a}^{b} \frac{f^{\prime \prime}(\xi)}{2}(x-a)(x-b) \mathrm{d} x
$$
根据 积分中值定理 , $\exists \eta \in[a, b] $ 使得,
$$
\int_{a}^{b} \frac{f^{\prime \prime}(\xi)}{2}(x-a)(x-b) \mathrm{d} x=\frac{f^{\prime \prime}(\eta)}{2} \int_{a}^{b}(x-a)(x-b) \mathrm{d} x=-\frac{(b-a)^{3}}{12} f^{\prime \prime}(\eta)
$$
梯形公式的误差公式得证。
多段梯形误差
考虑积分中常用的多段梯形近似
$$
\int_{a}^{b} f(x) d x \approx \sum_{i=1}^{n} \frac{1}{2}\left[f\left(x_{k-1}\right)+f\left(x_{k}\right)\right] \Delta x_{k}
$$
那么在某一段上它的误差为
$$
\begin{aligned} g\left(\Delta x_{k}\right) & =\frac{\Delta x_{k}}{2}\left[f\left(x_{k-1}\right)+f\left(x_{k-1}+\Delta x_{k}\right)\right] -\int_{x_{k-1}}^{x_{k-1}+\Delta x_{k}} f(x) d x\end{aligned}
$$
根据上文的结论,该误差可以写为
$$
g\left(\Delta x_{k}\right) =-\frac{\Delta x_{k}^{3}}{12} f^{\prime \prime}(\eta)
$$
若多段梯形为 $[a,b]$ 区间内均分为 $n$ 份的情况,那么 $\Delta x_k=\frac{b-a}{n}$,有
参考资料
文章链接:
https://www.zywvvd.com/notes/study/math/trapezoid-rule/trapezoid-rule/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付