图割 Graph Cut

Graph Cut 是一种用于 $n$ s维图像数据的边界优化和区域分割的分割技术，本文记录相关内容。

简介

• Graph Cut 通过交互式的或自动的定位一个或多个代表“物体”的点以及一个或多个代表“背景”的点来进行初始化—这些点被称作种子（Seed并被用于分割的硬约束（hard constraints）。另外的软约束（soft constraints）反映了边界和/或区域信息。

原理

• 每个像素视作二维平面上的节点，虚拟源、目标节点 $S, T$，图边分为两类，虚拟节点和每个图像像素的边，每个图像像素与其周围像素也有边连接，两种边权重定义如图：

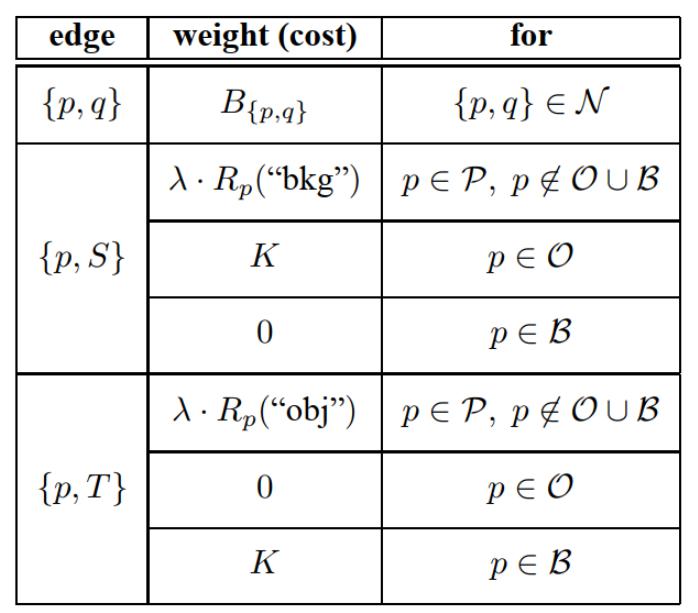
• 其中：

$$ K = 1+\max _{p \in \mathcal{P}} \sum_{q:\{p, q\} \in \mathcal{N}} B_{\{p, q\}} $$

• 将图像中所有像素 $p$ 的邻域边权值算出并求和，结果有像素个结果。选取最大结果再加1作为 $K$。而最大和在这里可粗略认为是聚类中的中心点，因为像素 $p$ 在此处邻域和最大，可认为 $p$ 点在此处与周围相邻像素及其相似，从而确保权值 $K$ 为最大权值）。

• ${p,q}$ 边表示相邻像素之间产生的边，边的权值为 $B{p,q}$，在上文中已经提到，当像素 $p$ 和 $q$ 相似时，产生的边的权值很大，反之产生的边的权值很小。当 $p,q$ 为两个相似像素时，边的权值很大，为了使得到的能量函数最小，因此该边不适合作为割边，因此符合逻辑。

• ${p,T}$ 边和 ${p,S}$ 边分为三种情况：

  1. $ p \in \mathcal{P}, p \notin \mathcal{O} \cup \mathcal{B} $ ，需要注意的是这里的 $O$ (前景）和 $B$ （背景）都是种子点，可认为是交互式方法划定的像素点，这类像素点需要软约束决定像素的归属。因此，边的权值应由软约束公式给出 $λ · R_p (bkg)$，注意这里求边 ${p,S}$ 边的权值
  2. $p ∈ O$，即 $p$ 是 $O$ 集合中的点，是交互式方法给定的前景像素点，这里我们可认为这个点就是前景的点，本文将前景种子点 $p$ 与 $S $ 的边的权值设为 $K$。即前景点与前景相连的边的权值为 $K$，$K$ 在这里是一个比1大的数。
  3. $p ∈ B$，即 $p$ 是 $B$ 集合中的点，是交互式方法给定的背景像素点，这里我们可以认为这个点就是背景点，本文将背景种子点与前景 $S$ 的边的权值设为0，可认为这个边权值是最小的，是可以作为割边的，事实上，这个边也是必定需要被割开的。

• 图的构造已经完全确定。我们通过对图的最小割确定图像中背景与前景的边界。

• 使用Graph Cut 算法时，给定需要分割的图像，在图像中定义前景像素区域，定义背景像素区域，至此形成了图，可以按照最小割的路径得到图像的分割结果。

原始论文

参考资料

• https://blog.csdn.net/webzhuce/article/details/99174355?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166838797016782425115550%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=166838797016782425115550&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allsobaiduend~default-2-99174355-null-null.142v63opensearch_v2,201v3control,213v2t3_control2&utm_term=graph%20cut&spm=1018.2226.3001.4187
• https://blog.csdn.net/lut609921895/article/details/56665368
• https://www.zywvvd.com/notes/study/algorithm/graph/max-flow-min-cut/max-flow-min-cut/

文章链接：
https://www.zywvvd.com/notes/study/image-processing/graph-cut/graph-cut/