本文最后更新于:2024年5月7日 下午
问题描述
- 假设我们有来自某一未知分布 $p$ 的随机变量观测样本集 $X$,如何从 $X$ 获取 $p$?
构造生成器还是评估器
- 对于某个分布,有两种方式可以描述这一分布
- 构造生成器:获取一个生产样本的生成器$g$,$g$ 生成的样本和 $p$ 的样本来源相同(不可区分)
- 构造评估器:构造一个样本评估器 $e$ ,对于给定的样本 $x$,$e$ 可以产生和 $p$ 相同的概率密度, $e(x) = p(x)$
直接构造评估器路线
-
解决上述问题的直观想法是构造一个关于参数 $\alpha$ 的分 $p_\alpha$,从其中选择与 $p$ 最接近的,那么就让他们作为评估器,给定相同样本输出与 $p$ 相同的概率密度就好啦~
-
但问题是我们不知道样本 $x$ 的真实概率密度 $p(x)$,而且难以保证对于所有可能的 $x$ 组成的集合 $X_{all}$,我们的 $\sum_{x\in {X_{all}}} p_\alpha(x) = 1$,这应该是不可能完成的约束,因此直接构造评估器的路线并不现实
ELBO 路线
-
如果我们有一组关于参数 $\beta$ 的生成器族 $g_\beta$,可以不断生成和 $x$ 维度相同的数据, 优化 $\beta$ 使得生成的数据和 $p$ 生成的数据难以区分,我们就可以说得到了 $p$ 的近似分布,GAN 基本上就延用了这个思路
-
如果我们觉得直接用模型描述 $X$ 分布困难或过于暴力,我们可以引入带有隐变量 $z$ 的概率分布,也就走上了 ELBO 的生成模型 道路
-
在ELBO 的生成模型中,我们为了描述复杂的概率分布引入了 $z$,建立了 $X,Z$ 的联合分布,但是这个 $z$ 却是个大麻烦,因为我们的目标是 $p$,这个分布和 $Z$ 无关,仅和 $X$ 有关,我们还得把 $z$ 消掉
-
直接的想法是对 $z $ 积分,$ p_{\theta}(x)=\int p_{\theta}(x \mid z) p(z) d z $,可以蒙特卡洛积分计算,但是如果要求精度会很慢,因此我们转向贝叶斯的思路,也就走上了 ELBO 贝叶斯评估器 的道路
-
ELBO 的神奇之处在于同时结合了生成器和评估器的分布描述方式,在多处受阻的境况中巧妙运用贝叶斯公式找到了一种可以参数化、可以优化、贪心最大化变量 (ELBO) 的方法
VAE
-
我理解 VAE 是对 ELBO 的直接实现
-
VAE 具象化了 ELBO 推导中的分布
-
$$
p(z) = N(0,1)
$$ -
$$
p(z|x)=N(z;\mu (x), diag(\sigma(x)^2))
$$
-
-
直接优化 ELBO
$$ \begin{aligned} ELBO &=\int_{z} q(z \mid x) \log \left(\frac{P(x \mid z) P(z)}{q(z \mid x)}\right) d z \\ &=\int_{z} q(z \mid x) \log \left(\frac{P(z)}{q(z \mid x)}\right) d z+\int_{z} q(z \mid x) \log P(x \mid z) d z \\ &=-K L(q(z \mid x) \| P(z))+\int_{z} q(z \mid x) \log P(x \mid z) d z \\ &=-K L(q(z \mid x) \| P(z))+E_{q(z \mid x)}[\log (P(x \mid z))] \end{aligned} \tag{12} $$ -
加入重参数化技巧实现训练过程
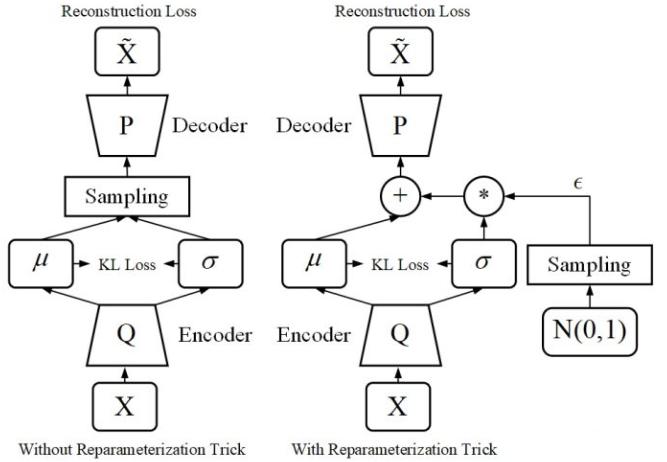
- 当训练完成时,生成器(解码器)可以依赖 $N(0,I)$ 上的采样生成近似 $X$ 的样本,也就得到了近似 $p$ 的生成器,以此近似描述 $p$ 的分布
实现
- 以瑞士卷(Swiss Roll) 数据作为目标分布 $p$
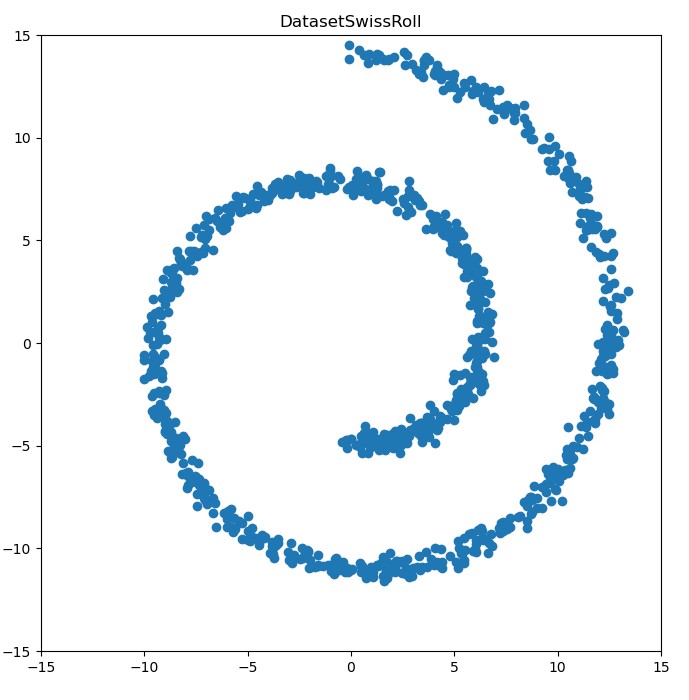
- 在
瑞士卷数据集上实现 VAE,构造模仿瑞士卷分布的数据生成器
核心代码
1 | |
代码仓库
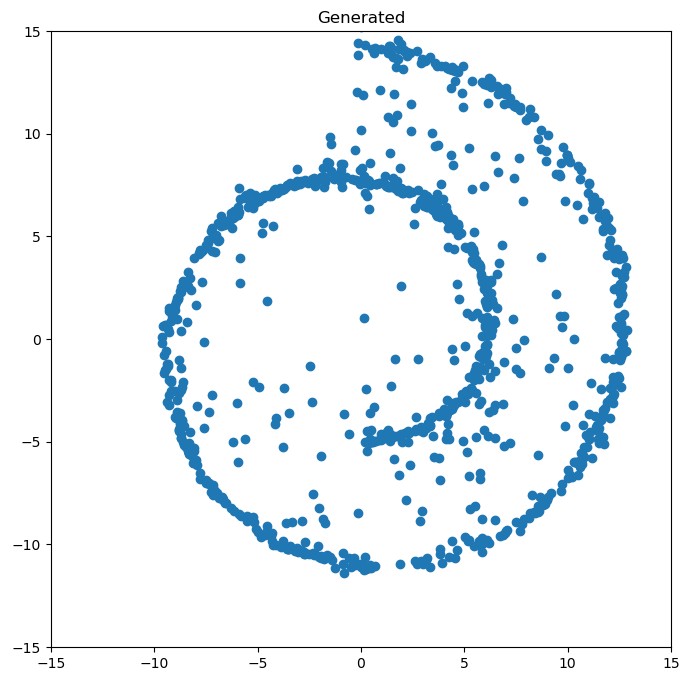
效果展示
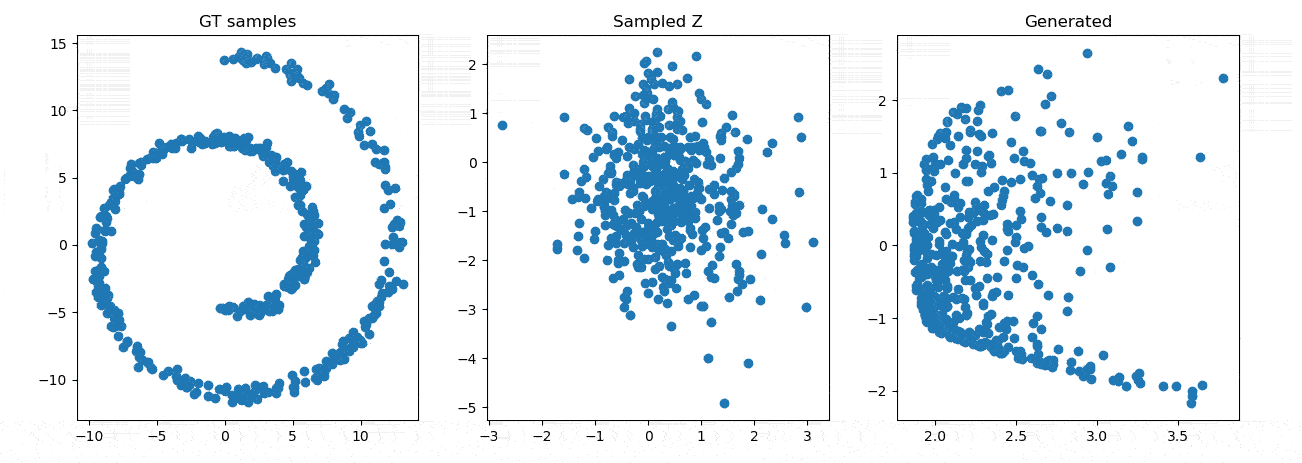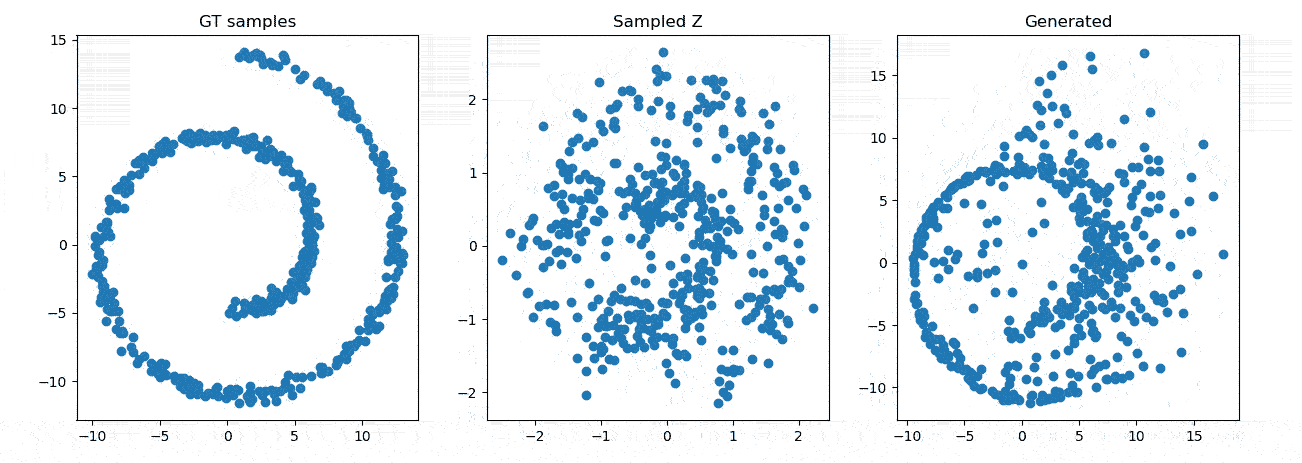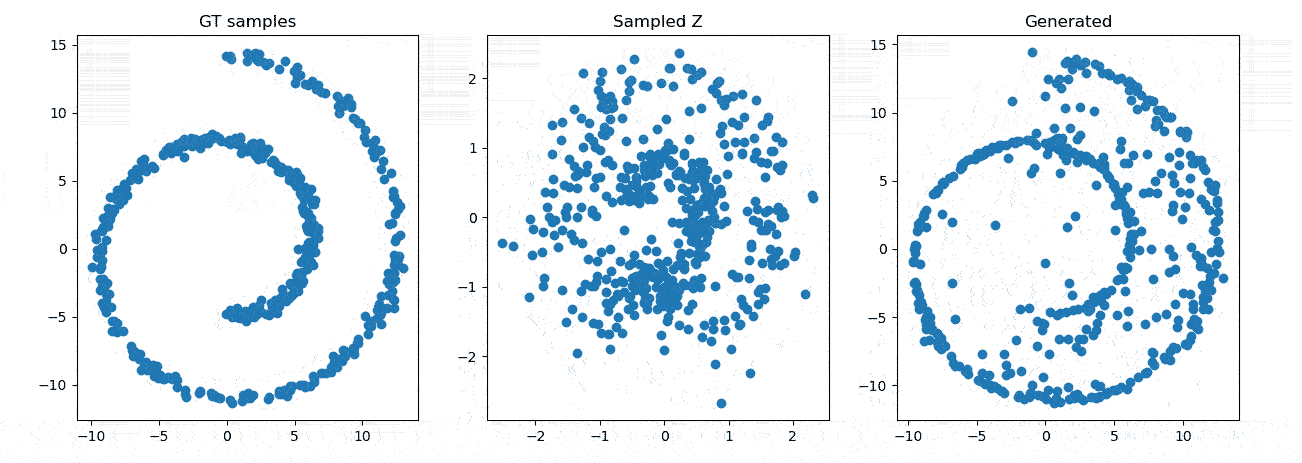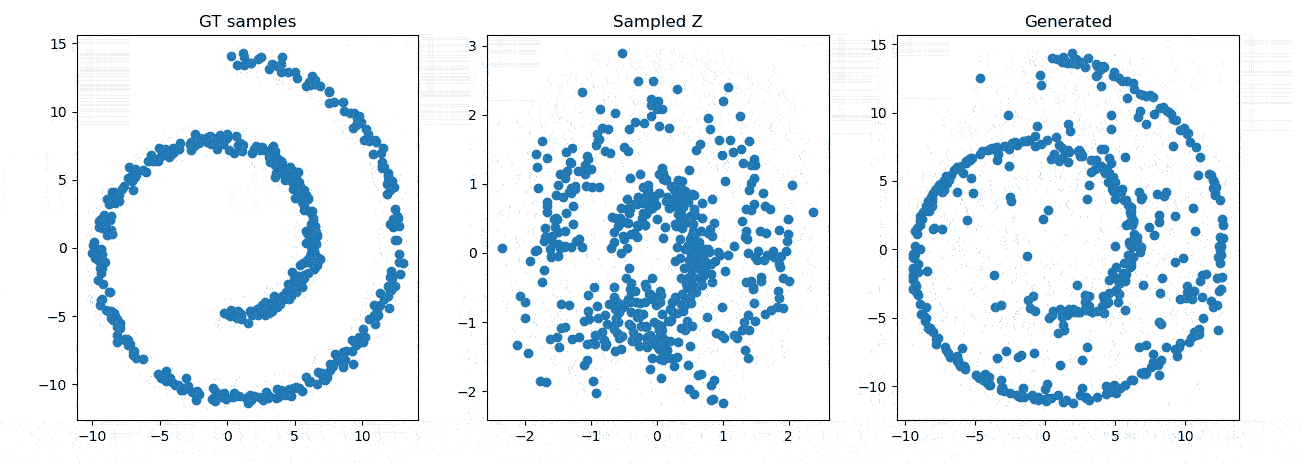
参考资料
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/generation/vae/vae-demo/vae-demo/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付