积分中值定理

本文最后更新于：2023年12月5日下午

在一元积分理论中，积分中值定理包括积分第一中值定理和积分第二中值定理.它们都是微积分学中的基本定理，本文介绍相关内容。

极值定理

极值定理也叫最大最小值定理，它的含义非常直观：如果函数 $f(x)$ 在区间 $[a,b]$ 上连续的函数，必然存在最大值和最小值，并且取到最大值和最小值至少一次。

我们假设 $m$ 和 $M$ 分别是区间 $[a, b]$上函数 $f(x)$ 的最小值和最大值，那么根据极值定理，可以得到以下式子成立：
$$
m(b-a) \leq \int_{a}^{b} f(x) d x \leq M(b-a)
$$

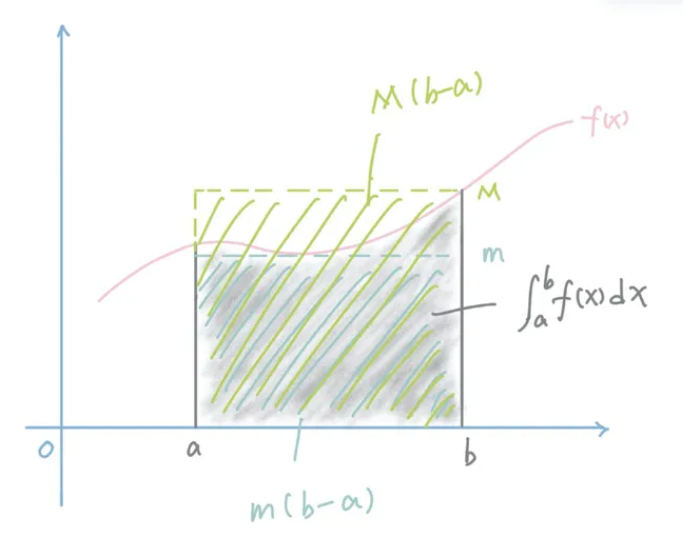
上图当中灰色阴影部分就是定积分的结果，蓝色的矩形面积是 $m(b-a)$，大的矩形面积是 $M(b-a)$。

由于m和M分别是最小值和最大值，所以我们可以得到
$$
\int_{a}^{b} m d x \leq \int_{a}^{b} f(x) d x \leq \int_{a}^{b} M d x
$$

第一积分中值定理

定义：
$$
\frac{1}{b-a} \int_{a}^{b} f(x) d x=f(\xi), \quad(a \leq \xi \leq b)
$$

证明

上述不等式两边同时除以 $b-a$，可以得到：
$$
m \leq \frac{1}{b-a} \int_{a}^{b} f(x) d x \leq M
$$
它的值位于函数在区间的最大值和最小值之间。根据连续函数的介值定理，我们一定可以在 $[a, b]$ 上找到一点$\xi $，使得 $ \mathrm{f}(\mathrm{x}) $ 在 $ \xi $ 这点的取值与这个数值相等，也就是说：
$$
\frac{1}{b-a} \int_{a}^{b} f(x) d x=f(\xi), \quad(a \leq \xi \leq b)
$$
上面这个式子就是积分中值定理了，这里有两点要注意:

函数必须是一个连续函数，否则的话，可能刚好函数在 $ \xi $ 点处没有定义。这个也是定理成立的先决条件。
连续函数的介值定理，它的含义是说对于一个在区间 $[a, b]$ 上连续的函数，对于任一在其最大值和最小值之间的常数，我们必然可以在区间 $[a, b]$ 上找到一点，使得该点的函数值等于这个常数。

也可以写成：
$$
(b-a) f(\xi)=\int_{a}^{b} f(x) d x, \quad(a \leq \xi \leq b)
$$

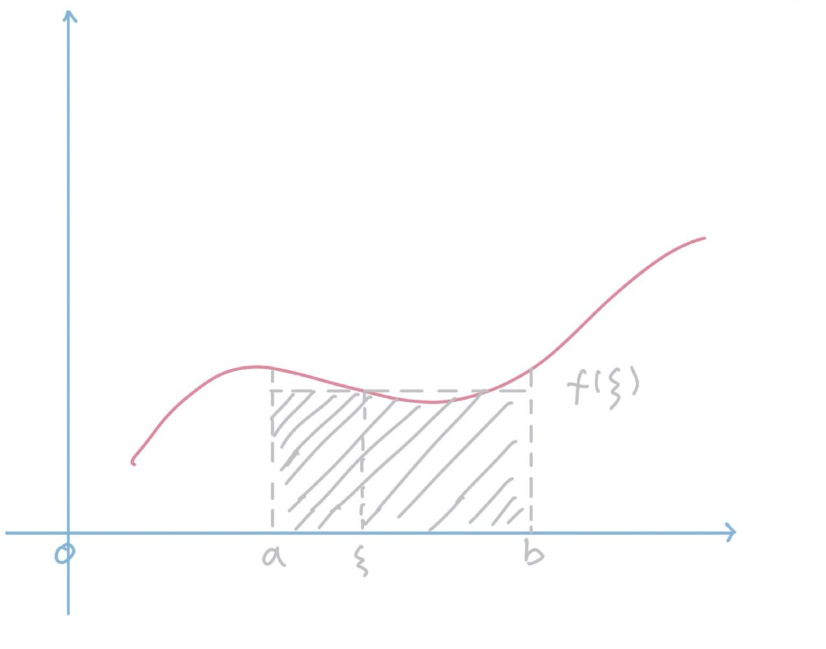
也就是说以 $ \alpha f(\xi) $为高的矩形面积和函数围成的曲形面积相等，所以它既是矩形的高，也是函数在 $[a, b]$ 上的平均值。

第一积分中值定理的推广

若函数 $f(x)$ 与 $g(x)$ 在闭区间 $[a，b]$ 上连续，函数 $g(x)$ 在 $[a，b]$ 上可积/连续且不变号，则 $[a，b]$ 在上至少存在一点$ξ$，使得
$$
\int_{a}^{b} f(x) g(x) d x=f(\xi) \int_{a}^{b} g(x) d x
$$

证明

由于 $g(x)$ 连续不变符号，不妨设 $g(x) \ge 0$

$f(x)$ 连续，则在 $[a,b]$ 区间内存在最大值 $M$，和最小值 $m$，则有：
$$
m\int_{a}^{b} g(x) d x \leq \int_{a}^{b} f(x) g(x) d x \leq M\int_{a}^{b} g(x) d x
$$
根据连续函数的介值定理，我们一定可以在 $[a, b]$ 上找到一点$\xi $，使得 $ \mathrm{f}(\mathrm{x}) $ 在 $ \xi $ 这点的取值与这个数值相等：
$$
m\int_{a}^{b} g(x) d x \leq \int_{a}^{b} f(x) g(x) d x=f(\xi)\int_{a}^{b} g(x) d x \leq M\int_{a}^{b} g(x) d x
$$

第二积分中值定理

各种形式的积分第二中值定理叙述如下：

设函数 $f(x)$ 与 $g(x)$ 在 $[a，b]$上可积

函数 $f(x)$ 在 $[a，b]$ 上单调增加且非负，则存在 $ \xi \in[a, b] $ ，使 $ \int_{a}^{b} f(x) g(x) d x=f(b) \int_{\xi}^{b} g(x) d x $.
函数 $f(x)$ 在 $[a，b]$ 上单调增减且非负，则存在 $ \xi \in[a, b] $ ，使 $ \int_{a}^{b} f(x) g(x) d x=f(a) \int_{a}^{\xi} g(x) d x $.
函数 $f(x)$ 在 $[a，b]$ 上单调，则存在$ \xi \in[a, b] $ ，使 $ \int_{a}^{b} f(x) g(x) d x=f(a) \int_{a}^{\xi} g(x) d x+f(b) \int_{\xi}^{b} g(x) d x $.