二值图拓扑性质 —— 多个物体

我们将处理视野中出现多个物体的情况：并且，我们还要开发一些更成熟的方法，用于从二值图中恢复信息。

概述

图像处理时，视野中经常会出现多个物体，对于图像中的各个区域，我们必须将它们以某种方式标注出来，然后，分别计算：各个区域的面积、一阶矩和二阶矩。

标注图像中的物体

特征函数

特征函数又被称为示性函数，即：给图像中的不同区域赋予不同的数值，数学上，特征函数可以被表示为：如果$ x \in \Omega_{i} $ ，那么，$I(x)=i$,其中$ \Omega_{i} $表示：图像中的第$i$个区域。

连通区域

如果我们可以找到：连接二值图中的两个点的一条路径，并且，在这条路径上，特征函数的取值是常数，那么，我们认为：这两个点是连通的。因此，在图中点A与点B是连通的，但是，它们都不与点C相连通。二值图中的连通区域是一个：关于连通点的最大的集合，也就是说，

1. 对于这个集合中的任意两点，都可以找到一条路径将它们连接起来;

2. 所有的连通点都包含在这个集合之中。

在图中，除了背景以外，总共有4个连通区域和4个洞。

标注

在离散二值图中，一种对“物体”进行标注的方法是：选取一个 $b_{ij}=1$ 的点，并且，赋予这个点以及和它连接在一起的点一个标记；下一步，对所有与这些标记点相邻的点（除了那些已经被标注的点以外）进行标注；然后，不断地重复下去。当这个递归过程完成以后，这个图像区域就被标注完毕了。紧接着，我们可以继续选择一个新的起始点，然后，对下一个图像区域进行标注。为了能够找到一个新的未标记区域，我们可以使用一种“对称”的方式，来对图像进行简单扫描。一旦发现：没有被标注的、并且 $b_{ij}=1$ 的点，我们就以该点作为新的起始点，然后，（对图像区域）进行标注。如果在对所有图像单元(即：像素点)进行扫描以后，还没有发现这样的点，那么，我们就完成了对二值图像中所有“物体”的标注。

连通性

首先，我们必须认真考虑：术语近邻点（具体）意思。假设我们使用正方形作为基本单元来对图像进行剖分，那么，在这种情况下，我们可以粗略地将近邻点“认为是”：和给定图像单元（即：像素点）的四条边相连接的四个图像单元。但是，我们应该如何看待：和给定像素点的四个角相连的四个像素点呢？因此，对近邻点的定义存在两种可能的情况，也就是说：

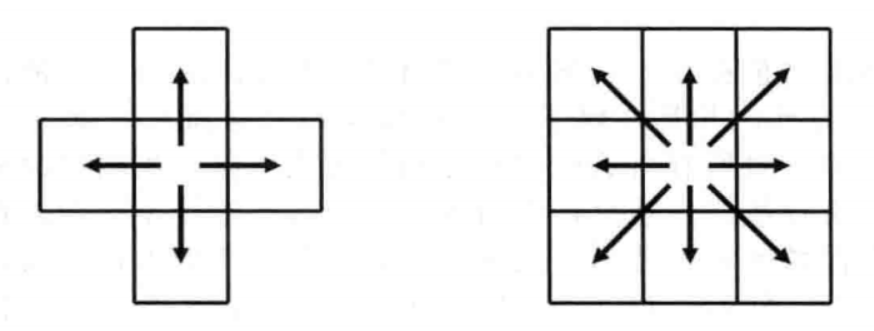
• 4一连接：只有和给定图像单元(即：像素点)的(4条)边相连的(4个)像素点，才被认为是（给定像素点）的近邻点。
• 8一连接：和给定图像单元的(4个)角相连的(4个)像素点，也被认为是（给定像素点）的近邻点。

事实上，这两种定义方式都不能完全令人满意。要看出这一点，我们需要明确的一点是：从背景中，我们也可以“分割出”一个连通区域。我们希望：对于离散二值图，我们从连续二值图中得出的、关于连通区域的直观感觉仍然适用。

我们可以用一条简单（不打结）的闭合曲线，将图像分割为两个简单的连通区域。这个结论被称为Jordan曲线定理。

现在，让我们来考虑一个包含4个值为1的像素点的简单图像。图中每一个值为1的像素点和中心像素点的边相连；而中心像素点的值为0，即：

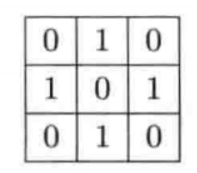
对于这种二值图，这是一个通过：去除“十字形”的中心点，从而形成的图形。如果我们选择使用4一连接，那么，我们会得到四个彼此不相连的物体区域。

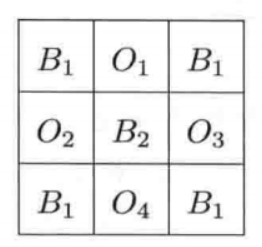
这四个彼此不相连的物体，肯定无法形成一条闭合曲线。然而，采用4一连接的方法，中间的那个作为背景的像素点($B_2$)，并不和其他的背景像素点($B_1$)相连，这与我们的直观感觉是相符的。因此，采样 4连接 的方法，我们得到了两个背景区域，但是，没有得到一条闭合曲线！

相反的，如果我们选择使用8一连接的方法，那么，图中的这4个(值为1的)像素点确实形成了一条闭合曲线，但是，中间的那个作为背景的像素点，却和其他四个背景像素点连接在了一起。我们得到了一条闭合曲线，但是，所得到的背景区域却只有一个，即：

解决这个悖论的一种方法是：对于物体使用4一连接，但是，对于背景使用8一连接（或者反过来）。这种对于物体和背景处理上的“不对称”，可能是我们所不希望看到的。我们可以通过：引入另外一种“不对称”，来避免：这种对物体和背景处理上的“不对称”。

1. 和给定像素点的4条边相连的四个像素点
2. 和给定像素点的4个角相连的4个像素点中的两个，定义为某一给定像素点的近邻点，即：

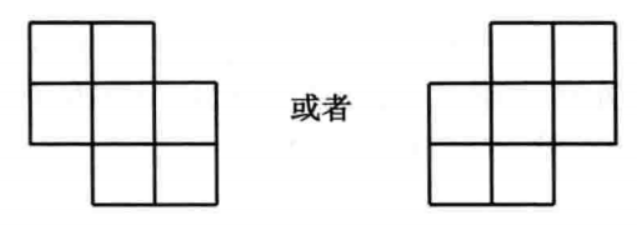
这两个和给定像素点的角相连的像素点，必须在同一条对角线上。这样做是为了保证像素点之间相互关系的对称，也就是说，如果像素点A是像素点B的近邻点，那么，像素点区域B也是像素点A的近邻点。从现在开始，我们将使用：上面所介绍的关于近邻点的两种定义方式中的第一个（即上图中的第一个），来确定像素点之间的连接关系。也就是说，我们将：给定像素点的上方、右方、右下方、下方、左方、左上方等6个方向上的、与该给定像素点相邻的6个像素点，定义为该给定像素点的近邻点。这种连接方式被称为 6一连接。

对于物体和背景，我们都使用6一连接的定义方式，就不会产生：使用4一连接和8一连接时所产生的、和连续二值图（的直观感觉）不一致的情况。如果我们使用正方形作为基本单元，来对图像进行剖分，那么，我们将使用这种6一连接的定义方式。

如果我们使用正六边形来对图像进行剖分，那么，问题就会变得简单得多。和某一个给定像素点相连的所有像素点，都是该给定像素点的近邻点，因此，不会出现“含混不清”的情况。我们上面的操作(即：关于6一连接的定义)可以被看作是：对正方形格栅进行简单扭曲，从而将其变为正六边形格栅的过程。为了看出这一点，我们将图像中某一特定行的上面一行像素点，整体向右移动半个像素宽度，然后，再将该特定行的下一行像素点，整体向左移动半个像素宽度，从而得到一个新的结构。现在，对于该特定行上的每一个像素点，其周围都正好有六个像素点与它相邻接，并且，这六个像素点正好是：上面所介绍的6一连接方式所确定的六个邻接点，如下图所示：

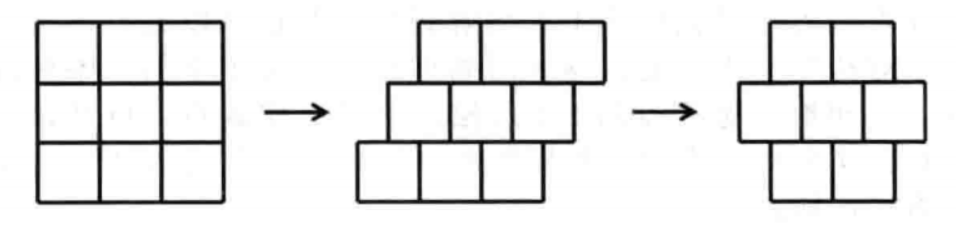
串行标注算法

现在，我们要介绍一种标注算法，这种标注算法更适于对图像进行串行扫描，并且，它不需要使用递归操作。我们约定：

1. 对图像进行逐行扫描，并且，行的编号顺序是从上到下的；
2. 对于每一行，我们按照从左到右的顺序，对该行中的像素点进行扫描。

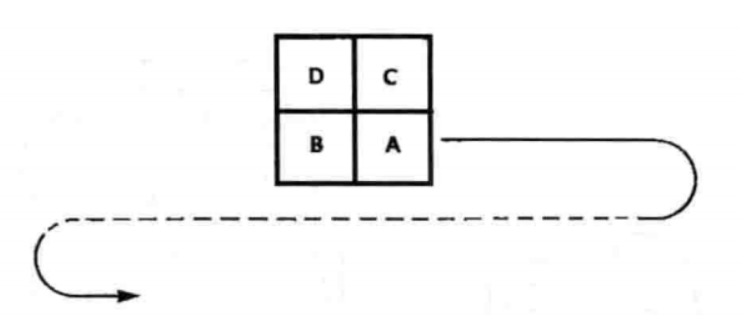
根据我们事先约定的扫描顺序，当我们扫描到某一个像素点A时，A点左边的像素点B已经被标注过了，并且，A点正上方的像素点C也被标注过了；此外，根据6一连接的定义，B点正上方的像素点D也是和A相连的，因此，我们还需要考虑D的标注结果。

为了简化问题，我们只对图像中的物体进行标注。如果A是0那么，我们不需要进行任何操作：如果A是1，并且，D点也被标注了(也就是说，D是（图像中的）物体上的点），那么，我们需要将D的标注结果(简称：标签)赋给A。类似的，如果点B或者点C也被标注了，那么，我们同样也需要将B或者C的标签复制给A.如果点B和C都没有被标注，并且，A是1，那么，我们必须选取一个新的标签，来对A进行标注。这表示：从A点开始，我们对一个新的物体进行标注。还有一种可能性是：B和C都被标注了。

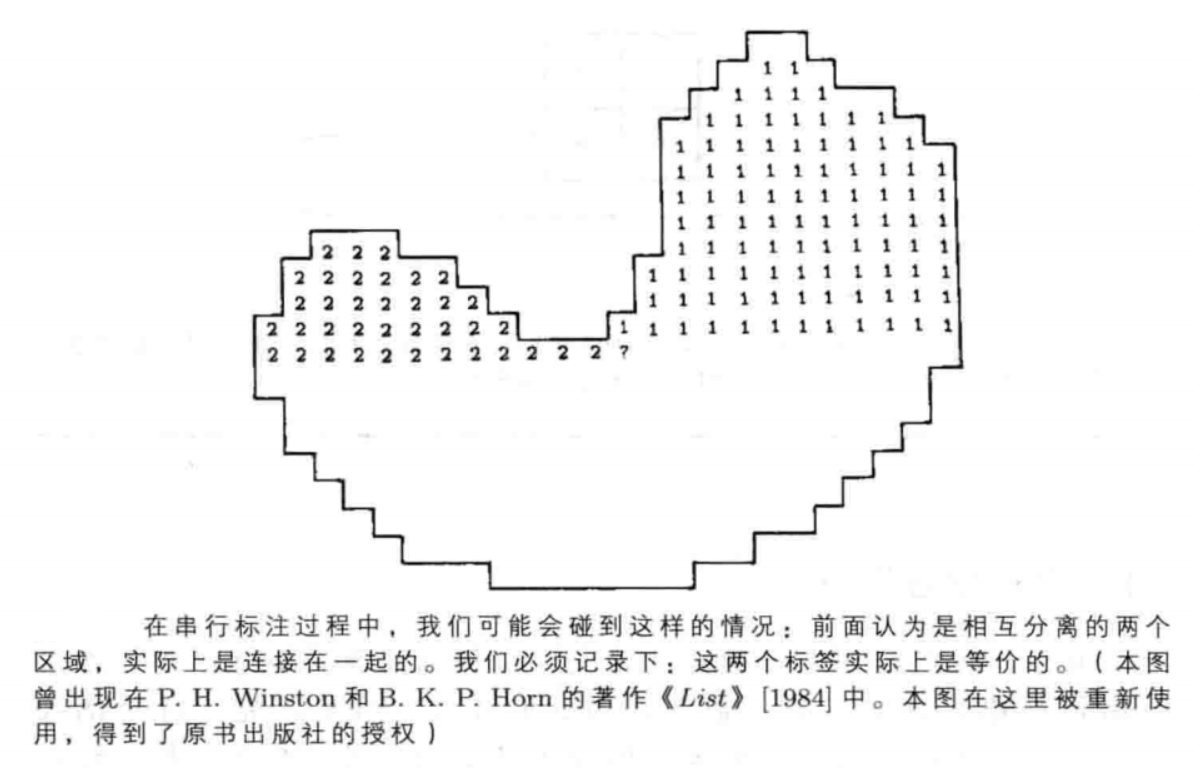
如果B和C的标签是相同的，那么，这并不会产生任何问题：但是，在我们关于6一连接的约定中，B和C是不相邻的，因此，B和C的标签有可能不同。对于这种情况，我们会将两个不同的标签赋予同一个物体。这意味着图像中的两个区域通过A点连接在了一起。此时，我们必须在A点做上新的“记号”，用来表示：A点上的这两个标签(即：B和C的标签)是等价的：然后，我们任意选取其中一个标签，来对A进行标注。对于串行标注算法，我们无法避开这个问题，这是串行标注算法必须付出的“代价”。

串行扫描结束后，我们需要将：图像中具有等价标签的各个区域，合并在一起。如果我们的目的是：计算区域的零阶矩、一阶矩以及二阶矩的总量，那么，我们甚至可以绕过区域合并这一步，而只需要简单地将：等价标签所对应的各个（等价）区域的零阶矩、一阶矩、二阶矩的计算结果，分别对应地加在一起即可。

如果我们想要让图像中的各个区域都具有唯一的标签，那么，我们需要对串行扫描结果进行二次扫描，从而将同一个具有代表性的标签赋予：具有等价标签的多个区域。我们可以从该区域所拥有的多个等价标签中，随机选取出的一个标签，来作为该等价区域的标签。

参考资料

• 伯特霍尔德・霍恩著 BERTHOLDKLAUSPAULHORN. 机器视觉[M]. 中国青年出版社, 2014.

文章链接：
https://www.zywvvd.com/notes/study/image-processing/robot-vision/chapter-4/multi-obj/multi-obj/