二值图拓扑性质 —— 局部计数

本文最后更新于：2024年1月14日晚上

为了提高速度和充分利用大规模积分电路的性能，我们同时还需要考虑：通过将局部算子并行地作用于二值图，我们可以对什么量进行计算。

局部计数

对于一个二值轮廓，我们可以通过对局部像素点的值求和来确定轮廓的面积，通过局部特征求和我们还可以得到图像的周长。我们只需简单地累计：图中和值为1的像素点相连接的、并且值为0的像素点的个数，就可求出图中区域的周长。

相应的局部算子有两个：一种用于检验“行”中的相邻像素点，另一种用于检验“列”中的相邻像素点。每一种局部算子的输出都是：两个输入值的异或运算$(α⊕b)$的结果。对所有局部算子的输出结果进行求和，我们就得到了一个关于（图像区域的）周长的估计值。

除了面积和周长以外，通过使用局部计数方法，我们还可以计算Euler数。Euler数的定义为：“体”的个数减去“洞”的个数。

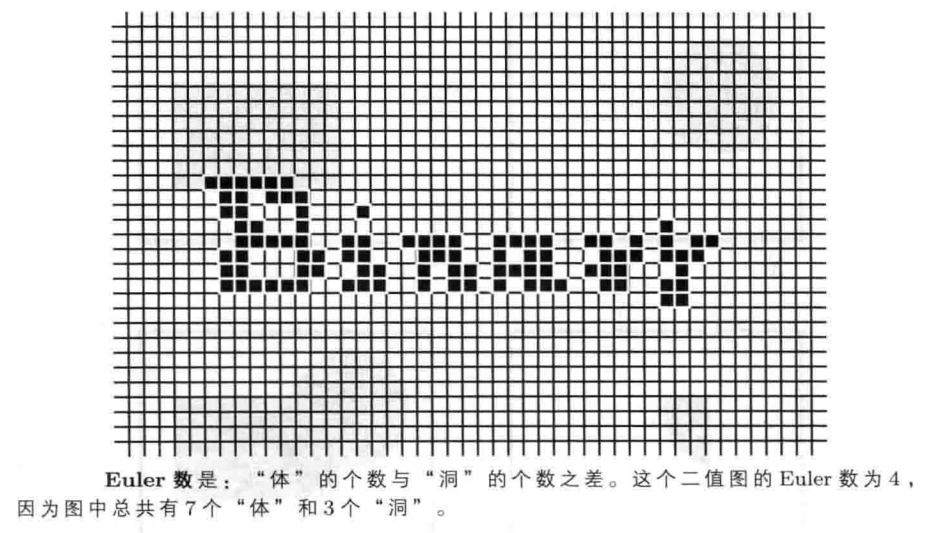
例如，大写字母“B”的Euler数为-1，因为它包含：一个“体”和两个“洞”：而小写字母“i”的Euler数为2：小写字母“n”的Euler数为1,等等。我们可以通过局部求和来计算Euler数，这个结论看起来似乎很奇怪。因为，无论是“体”的数目还是“洞”的数目，都无法通过局部求和计算出来，但是，对于它们的差(即：Euler数)，却是可以通过局部求和计算出来的。

集合可加性

我们可以通过一些方法，将二值图组合在一起。例如，我们可以对它们取“或”，其结果是：这两个图像区域的“合并”：我们也可以对它们取“与”，其结果是：两个图像区域的“重合”部分。一个有趣的问题是：经过这些组合操作所得到的图像的性质，和原始图像的性质比起来，有多大的区别？我们之所以对这个问题感兴趣，其中的一个原因是：我们希望将图像分解成很多小的部分；然后，对这些（小的）部分进行并行处理；最后，再将这些并行处理的结果合并在一起。如果我们用X和Y来表示原始图像，并且，将X和Y的逻辑或(V)和逻辑与(A)分别记为：$X∩Y$ 和 $X∪Y$ ，那么，它们之间的面积关系满足：
$$
A(X)+A(Y)=A(X \cup Y)+A(X \cap Y)
$$
这是因为，X和Y的面积总和等于：它们“合并”后的（图像区域的）面积再加上它们的“重合”部分的面积。在二值图中，满足这个条件的测量值被称为：具有集合可加性的测量值。周长就是一个满足这个条件的测量值。因为：X和Y的周长的总和等于：它们“合并”后的区域的周长再加上它们的“公共边界”的长度。碰巧的是，Euler数也满足这个条件。正是出于这个原因，我们可以通过：局部处理结果的“相加”，来求得这三个量。

集合可加性使得我们可以：将一幅图分割为许多小块：然后，将对这些小块的处理结果合并到一起，从而得到对整张图像的处理结果。我们将以求图像的Euler数为例，来演示这个过程。

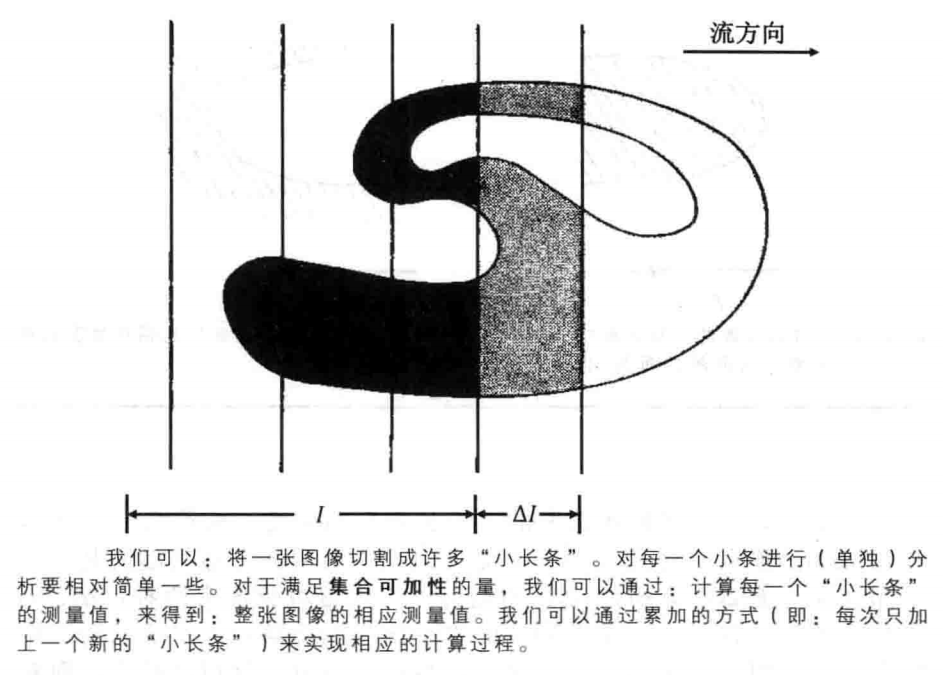
首先，让我们来考虑一张连续的二值图。我们在图中选定一个方向，并且，将这个方向称为流方向。现在，我们沿着垂直于流方向的方向，用直线将图像切分为许多“小长条”。对于所有满足集合可加性的量，我们每一次只考虑一个“小长条”，然后，将本次计算结果和前面的计算结果进行累加。通过这种方法，我们可以逐步地计算出：关于整张图的“整体”结果。

我们用$△I$来表示：每一次处理的“小长条”，用$I$来表示：到目前为止已经计算完的那部分图像（即：前面已经处理完的所有“小长条”所组成的集合）。由于Euler数满足集合可加性，因此，我们可以得到：
$$
E(I \cup \Delta I)-E(I)=E(\Delta I)-E(I \cap \Delta I)
$$
我们所真正感兴趣的是：图中那些使得$E(△I)≠E(I∩△)$的地方。出现这种情况有两种可能：

“小长条”中包含：一个新物体的“头部”一小块；
“小长条”中包含：一个洞的“尾部”一小块。

这两种“小块”分别被称为：面对流方向的凸面和面对流方向的凹面。

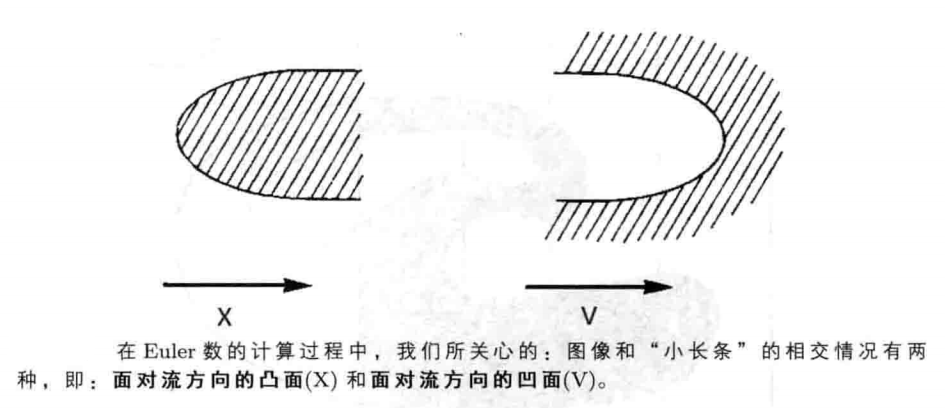
对于第一种情况(即：面对流方向的凸面)，其Euler数的变化(简称Euler差值)为：
$$
\Delta E=E(\Delta I)-E(I \cap \Delta I)=1-0=1
$$
对于第二种情况(即：面对流方向的凹面)，其Euler差值为：
$$
\Delta E=E(\Delta I)-E(I \cap \Delta I)=1-2=-1
$$
注意：$I$和$△I$刚好“贴”在一起，因此，它们的交$I∩△I$是一条线段。整张图像的 Euler 数等于$X-V$,其中，$X$ 是面对流方向的凸面的数目，$V$ 是面对流方向的凹面的数目。

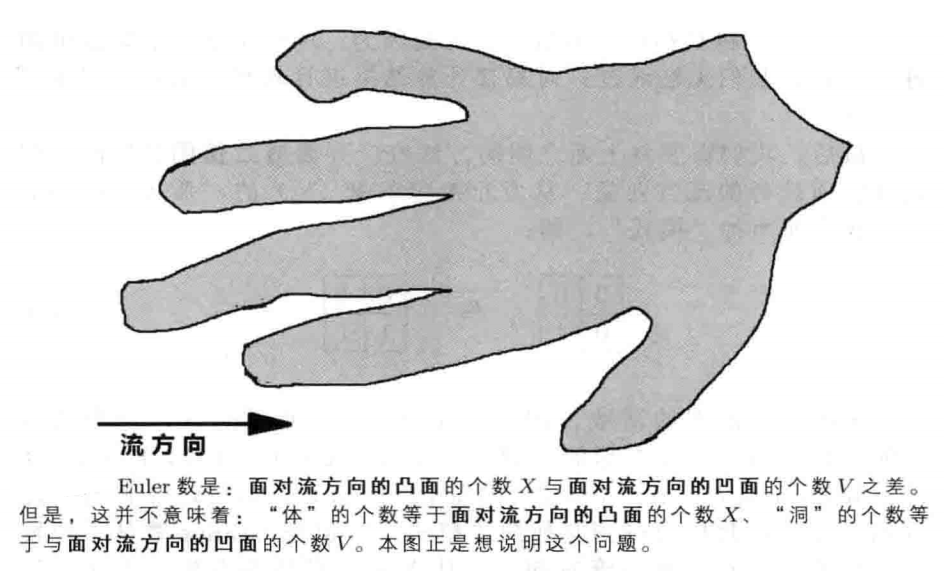
值得注意的是：在前面，我们给出了Euler数的另一个定义，即：图中“体”的数目 $B$ 与洞的数 $H$ 的差。这两个定义是等价的，但是，这并不等于说：$B$ 一定等于 $X$、并且$H$一定等于$V$。通过考虑：有很多“突出”的单一物体，我们可以很容易地看到这一点。在图中，$X$ 和 $ V$ 都很大(并且$X=V+1$ ),但是，$B=1,H=0$。这里，我们需要指出的是，不会出现：$B$ 和 $H$ 都很大、但是X和V都很小的情况。这是因为：$B$ 和 $H$ 不满足集合可加性，因此，我们无法通过：对局部计算结果进行求和，来得到整体的 $B$ 和 $H$.

最后，我们需要将上面介绍的方法推广到离散二值图的情况。假设我们所选择的流方向是：从西北指向东南的，那么，我们需要寻找下面两种“模式”，即：

在图像中出现的次数，例如，如果一个二值图包含：一个长方形的“体”和一个长方形的“洞”，那么，$X=1$ ,并且，$V=1$ ;

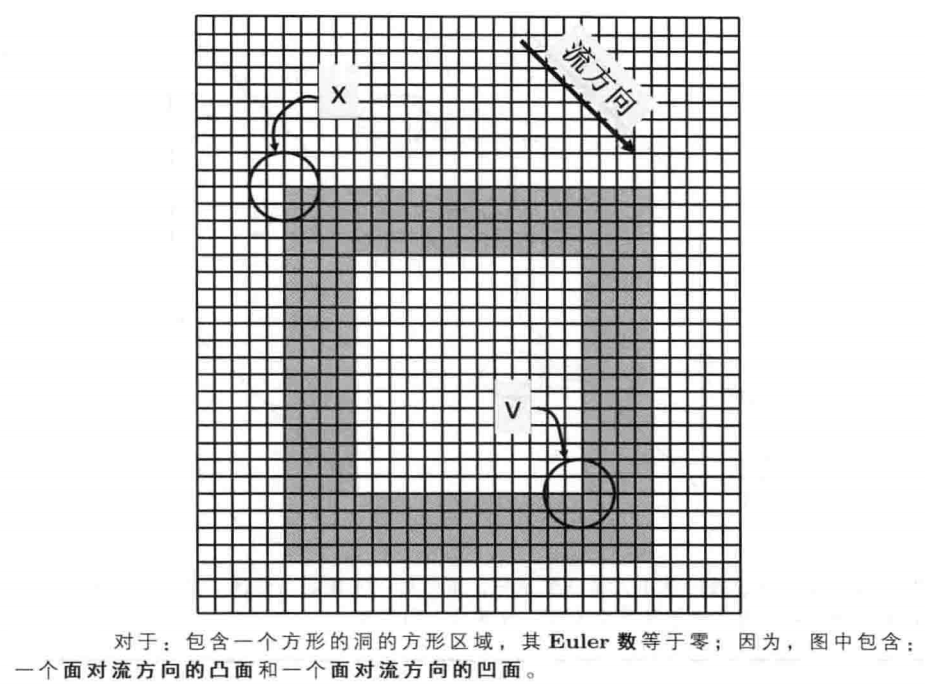
因此，其Euler数$E=X-V=0$。如果选择其他的流方向，那么，我们会得到其他的“模式”，但是，Euler数是不会发生变化的。（对于新的流方向，即使 $X$ 和 $V$ 的值都发生了变化，但是，它们的差始终保持不变）。

Euler 数可加性示例

采用“手形”的示例图像，拆分成小图计算整体图像 Euler 数：

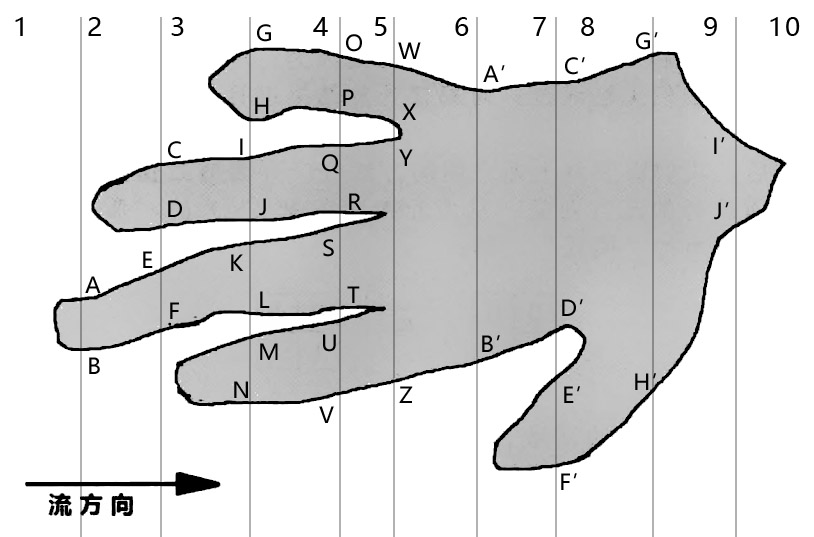
将原图分为十个小区域，整个图的欧拉数显然为 1，之后我们分别计算十个区域的欧拉数，作为欧拉数可加性的示例和验证。

区域编号	$E(\Delta I)$	$E(I \cap \Delta I)$	$\Delta E$	说明
1	1	0	1	$I$ 此时为空
2	2	1	1	$I \cap \Delta I$ 为 $AB$ 线段
3	4	2	2	$I \cap \Delta I$ 为 $CD,EF$ 线段
4	4	4	0
5	2	4	-2	小区域有两个连通域，$I \cap \Delta I$ 为四段线段
6	1	2	-1
7	2	1	1
8	1	2	-1
9	1	1	0
10	1	1	0