本文最后更新于:2024年5月7日 下午
本文记录《机器视觉》 第三章第三节 —— 投影,一些学习笔记和个人理解,其中核心内容为二值图的投影。
- 根据 转动惯量 节的结论,我们只需要使用一阶矩和二阶矩,就可以计算出:物体的位置和朝向。为了计算物体的一阶矩和二阶矩,我们并不需要知道原始图像,因为,原始图像的投影已经提供了充足的信息。这是一个有趣的结论,因为,图像投影的形式更加紧凑,并且,可以用来设计快速算法。
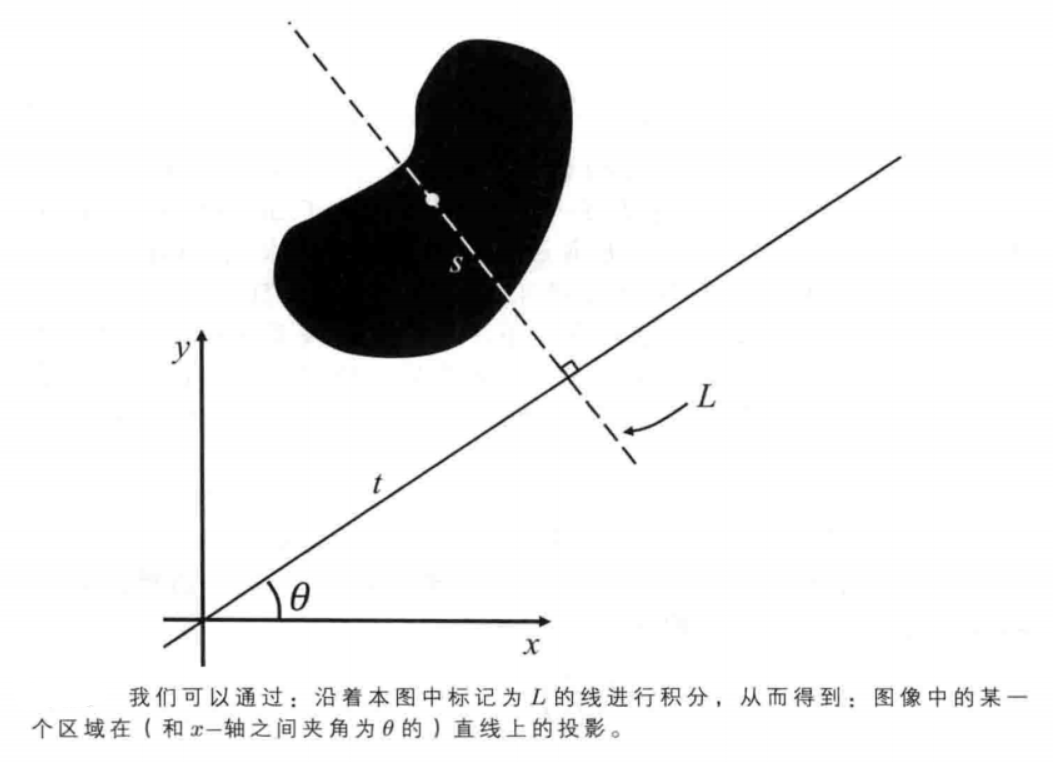
- 考虑一条经过原点并且与 $x$ 轴之间的夹角为 $\theta$ 的直线。现在,我们构建一条新的直线,这条线和原来的直线垂直,并且和原来的直线相交于:和原点之间距离为 $t$ 的一点。我们用 $s$ 来表示:从两条线的交点开始、沿着新的直线所“走过”的路程。沿着新的直线对 $b(x,y)$ 进行积分,就给出了一个投影值,也就是说:
$$
p_{\theta}(t)=\int_{L} b(t \cos \theta-s \sin \theta, t \sin \theta+s \cos \theta) d s
$$
- 这个积分是在直线 $L$ 所在的图像“区域”上进行的。
- 例如竖直方向的投影(即:$\theta = 0$) 为:
$$
v(x)=\int_{L} b(x, y) d y
$$
- 水平方向的投影(即:$0=π/2$)为:
$$
h(y)=\int_{L} b(x, y) d x
$$
- 由于:
$$
A=\iint_{I} b(x, y) d x d y
$$
- 因此我们有:
$$
A=\int v(x) d x=\int h(y) d y
$$
- 此外还有:
$$
\bar{x} A=\iint_{I} x b(x, y) d x d y=\int x v(x) d x
$$
$$
\bar{y} A=\iint_{I} y b(x, y) d x d y=\int y h(y) d y
$$
- 因此,投影的一阶矩等于原始图像的一阶矩。
- 为了计算朝向,我们还需要计算图像的二阶矩。通过投影,我们可以很容易地计算出:这些二阶矩中的其中两个,也就是说:
$$
\iint_{I} x^{2} b(x, y) d x d y=\int x^{2} v(x) d x
$$
$$
\iint_{I} y^{2} b(x, y) d x d y=\int y^{2} h(y) d y
$$
- 但是,只使用水平投影和竖直投影,我们无法求出:对$xy b(x,y)$的积分。我们可以添加对角投影(即:$\theta=π/4$)来解决这个问题:
$$
d(t)=\int b\left(\frac{1}{\sqrt{2}}(t-s), \frac{1}{\sqrt{2}}(t+s)\right) d s
$$

- 根据 $x=t\cos\theta-s\sin\theta,y=t\sin\theta+s\cos\theta$,有:
$$
t=(x+y) / \sqrt{2} , s=(y-x) / \sqrt{2}
$$
- 因此有:
$$
\iint_{I} \frac{1}{2}(x+y)^{2} b(x, y) d x d y=\iint_{I} t^{2} b\left(\frac{1}{\sqrt{2}}(t-s), \frac{1}{\sqrt{2}}(t+s)\right) d s d t
$$
- 进一步可以得到:
$$
\iint_{I} \frac{1}{2}(x+y)^{2} b(x, y) d x d y=\int t^{2} d(t) d t
$$
- 由于:
$$
\iint_{I} \frac{1}{2}(x+y)^{2} b(x, y) d x d y=\iint_{I}\left(\frac{1}{2} x^{2}+x y+\frac{1}{2} y^{2}\right) b(x, y) d x d y
$$
- 因此可以得到:
$$
\iint_{I} x y b(x, y) d x d y=\int t^{2} d(t) d t-\frac{1}{2} \int x^{2} v(x) d x-\frac{1}{2} \int y^{2} h(y) d y
$$
- 因此,通过使用“水平”、“竖直”和“对角线”三个方向的投影,我们可以计算出一阶矩和二阶矩,并且,最终确定图像区域的位置和朝向。
参考资料
- 伯特霍尔德・霍恩著 BERTHOLDKLAUSPAULHORN. 机器视觉[M]. 中国青年出版社, 2014.
文章链接:
https://www.zywvvd.com/notes/study/image-processing/robot-vision/chapter-3/projection/projection/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付