二值图拓扑性质 —— 迭代修正

本文最后更新于：2024年1月14日晚上

除了将二值图中的局部处理结果直接加起来以外，我们还可以用这些局部处理结果来生成一张新的二值图。本文记录生成二值图的原则和一种并行策略。

迭代修正

除了将二值图中的局部处理结果直接加起来以外，我们还可以用这些局部处理结果来生成一张新的二值图。根据原图中的对应图像单元的局部计算结果，我们可以确定：新的二值图中相应图像单元的值。新的二值图可以被作为：另一个计算周期的输入。这个操作被称为：迭代修正。

迭代修正方法非常有用，因为它使得我们可以将：那些很难直接使用局部计数法来进行处理的图像，逐步地转化为：可以使用局部计数法来进行处理的图像。

通过类似迭代腐蚀的操作，我们有可能“蚀刻”出物体的边界，从而，最终得到一张“骨架”图。所谓“骨架”图是指：经过蚀刻以后，一幅图中所剩下的部分。在蚀刻过程中，图像中的许多图像单元（即：像素点）都被“侵蚀”掉了。蚀刻过程的终止条件为：如果继续侵蚀掉图中的任何一个图像单元，都会改变原图的连通关系。避免对最后得到素描图继续进行侵蚀，是非常重要的。为了解决这个问题，我们需要考虑：当我们改变图像中的某一个像素点的值时，Euler数会发生什么变化。那些不改变Euler数的操作被称为是守恒的。

幸运的是，由于Euler数满足集合可加性，因此，Euler差值只依赖于：某一个图像单元的邻域。我们假设：某一个图像单元的灰度值为零，并且，它邻域内的所有图像单元的灰度值都为零：如果我们将该图像单元的灰度值从0变为1：

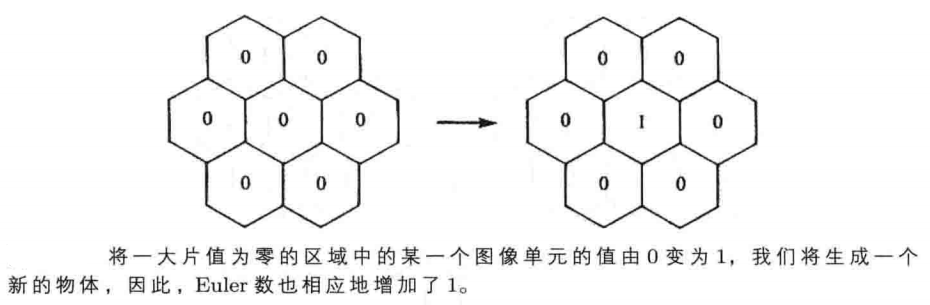
那么，这个操作将会使得图像的Euler数增加1。这个结果并不依赖于：该图像单元邻域以外的其他图像单元上的值。类似地，如果在某一图像单元的邻域中，只有一个图像单元的值为0(或1)，那么，改变该图像单元的值，Euler 数不会发生变化：因为，这个操作只是“扩大”一个物体（或缩小空洞）。

在我们的方法中，每一个图像单元的周围都有六个图像单元和它相连(我们将其称为“邻居”)。每一个“邻居”的值可以为0或1.因此，总共有$2^6=64$种可能的邻域结构。对于每一种邻域结构，我们都可以计算其 Euler 差值$E*$,即：当邻域中心的图像单元由0变为1时，该邻域的Euler 数所发生的变化（当邻域中心的图像单元由1变为0时，该邻域的Euler差值为：$-E*$)。

我们所特别感兴趣的是：那些 $E*=0$ 的邻域结构，因为，我们可以任意改变这些邻域的中心像素点上的值，而不改变其Euler数。我们可以将这64种邻域结构，分为如下5种情况：

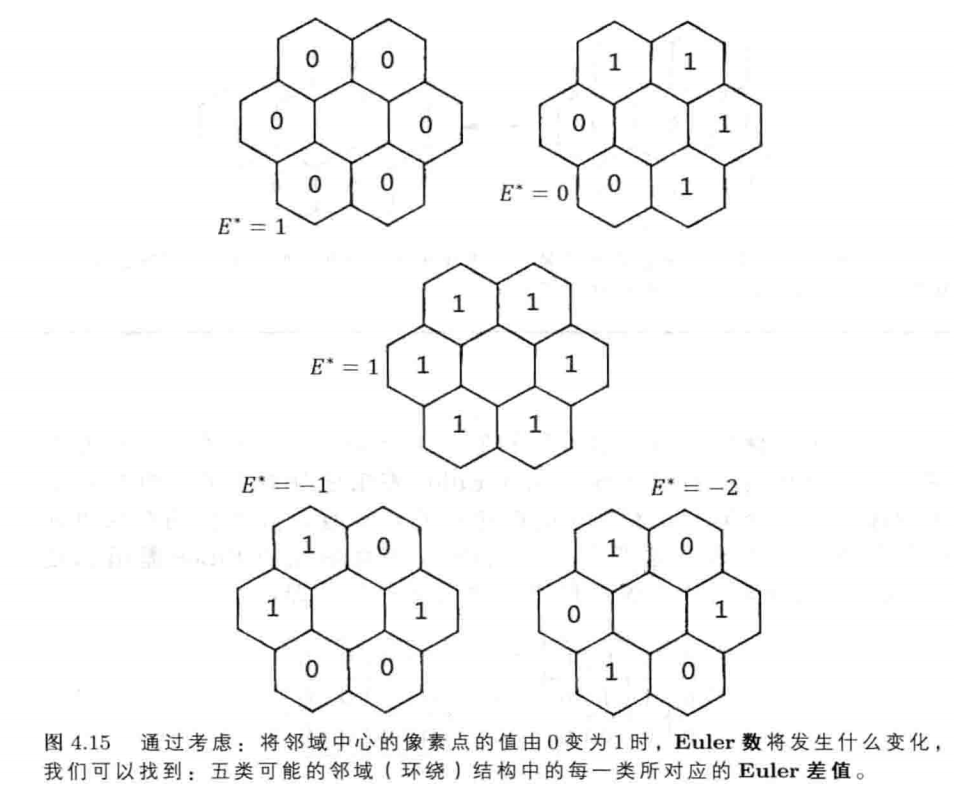
$E*=+1$: 六个“邻居”的值全为0。这种情况对应于：中心像素点的值的变化(即：由0变为1)，将产生出一个新的物体;
$E*=+1$: 六个“邻居”的值全为1。这种情况对应于：中心像素点的值的变化(即：由0变为1)，将填满一个洞;
$E*=0$: 我们将这六个“邻居”看作一个圆周序列，那么，这个圆周序列刚好能被分割为两个子序列：并且，其中一个子序列的值全为1，而另一个子序列的值全为0;
$E*=-1$: 圆周序列包含：两个值全为1的子序列，并且，这两个子序列被两个值全为0子序列“隔开”。在这种情况下，中心像素点的变化(即：由0变为1)对应于：两个物体被连接在一起（成为一个物体），或者，一个洞被“分”为两个洞。
$E*=-2$: 三个0和三个1彼此间隔地排列成一个圆周序列。这种情况下，中心像素点的变化(即：由0变为1)对应于：三个物体被连接成为一个物体：或者，一个洞被“分割”为三个洞。

因为每个图像单元只有6个邻居，因此，上面5种情况，包含了所有可能出现的情况。我们根据Euler数的变化，将这些特殊的邻域结构
分别记为：$ N_{+1}, N_{0}, N_{-1} $ 和 $ N_{-2} $.

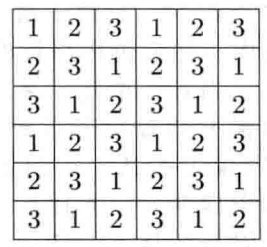
此外，我们还有一个难题没有解决。在使用并行方式对图像进行处理时，我们可能在“不知不觉”之中，就改变了其Euler数。这是因为：一个图像单元的“邻居”的值，可能会在“不知不觉”中发生变化，从而使得：对该图像单元的Euler差值的计算失效。如果我们用串行方式来进行处理，那么，将不会出现这种问题。当然，我们并不想要对图像进行串行处理。解决这个问题的另一种方法是：将图像分割为：许多交织在一起的子域，从而使得：图像单元的“邻居”位于不同的子域中；然后再用串行的方式对子域进行处理。

如果我们以正方形（作为基本单元）来对图像进行剖分，那么，要保持Euler数不变，所需要的最小子域数为3。我们可以使用周期序列$1,2,3,1,2,3…$来对图像中的某一行图像单元(即：像素点)进行编号；对于下面一行的图像单元，其标注方式和这一行类似，只是编号从2开始：再下一行的编号从3开始。根据我们所使用的关于邻域的定义，图像单元和它的“邻居”的编号是不同的。我们用三种不同颜色来对：正六边形剖分方式，进行编号。之后可以分别并行处理组1，组2，组3的像素。