本文最后更新于:2024年5月7日 下午
许多机器视觉算法都只针对:由单个物体的表面所生成的图像。如果一个物体表面的图像没有覆盖整个视野,那么,我们必须想办法找出:相应的物体表面所对应的图像区域。
阈值
为了将一张灰度图变成一张二值图,我们需要设定一个阈值。我们希望找到一种自动方法,对于各种不同情况(例如:不同的光照情况,或者,不同的物体表面反射性质),它都能够自适应地进行处理。对于这个问题,一种处理方式是:只分析图像中灰度值的情况,而不去管图像单元的位置。
对于一张连续图像,我们可以定义图像的亮度分布函数,记为$p(x)$。对于一个很小的, $ \delta x $图像中亮度值大于等于x而小于$ x+\delta x $的那一小部分区域的大小是$p(x)δx$。累积亮度分布函数$P(x)$ 是:对亮度分布函数的积分。对于一个给定的$x$, 累积亮度分布函数$P(x)$是指:图像中亮度小于等于x的那一部分区域的大小,即:
$$
P(x)=\int_{0}^{x} p(t) d t
$$
对于一幅数字图像,我们可以得到其灰度值统计直方图,它给出了:具有某一灰度值的图像单元(即:像素点)的个数。通过对灰度值统计直方图进行求和,我们可以得到累积灰度值统计直方图。这些工具在这里会变得非常有用。
统计直方图
实际上,物体所对应的像素点的灰度值,并不完全相同。这是由许多因素造成的,其中包括测量噪声。在确定灰度值的过程中,我们需要测量:由入射光子所激发的、数量相对较少的电子,这个测量结果中存在误差。此外,用于对电量(测量结果)进行放大的仪器会产生更多的噪声。这种噪声效应将会“抹平”(灰度值的)概率分布。更准确地说,我们所得到的测量结果是:“理想的”概率分布与加性噪声的概率分布之间的卷积结果。所谓“理想的”概率分布是指:在没有噪声的情况下所得到的概率分布。通常情况下,图像传感器对每一个图像单元的响应并不完全相同:此外,物体表面的反射率也不是完全相同的:还有,光照情况也不完全相同。出于这些原因,我们所设计的阈值标准,必须允许:物体和背景的灰度值在一定范围内发生“波动”变化。
如果我们幸运的话,这个“波动”变化的范围较小,我们仍然能够找到一个阈值,将物体和背景所对应的两组灰度值分开。要找到这个阈值,我们需要借助于:灰度值的统计直方图。我们所期待看到的是:在灰度值的统计直方图中,会出现两个峰值,它们分别与图像和背景基本对应,并且,在两个峰值之间,会有一个“山”将其隔开。

理想情况是:在统计直方图的两个峰值之间有一个间隔。但是,即使统计直方图的两个“山峰”之间有重叠的部分,我们也可以将阈值选为:(统计直方图中)统计值最小的位置(即:图像中,具有该亮度的像素点的数目最少)。这使得我们可以:以很小的分类错误率将灰度图变为二值图。
到目前为止,我们假设:统计直方图中的每一个“竖条”都对应于一个灰度值。通过将“近似相等”的灰度值合并到一起,我们可以得到一个粗糙的统计直方图。在建立统计直方图时,我们总要面对一个难题:统计直方图中的“竖条”到底应该取多宽?每一个“竖条”所给出的是:灰度值在该竖条所对应的取值范围内的图像单元的数目。如果“竖条”太宽,那么灰度值的分辨率会变得很低(一个极端的情况是:只有一个“竖条”,此时,完全无法对灰度值进行分辨)。如果“竖条”取得太窄,那么,每个“竖条”将会只包含几个元素,此时,统计直方图会变得太“零碎”(一个极端的例子是:几乎所有“竖条”的高度都为零,只有一些不是零)。对于这种情况,我们很难确定:统计直方图中“高度”最小的“竖条”的位置。自然地,当物体在图像中“占据”一大片区域时,这个现象并不明显。通常,我们需要将统计直方图中相邻的“竖条”合并到一起,从而实现统计直方图的光滑化;但是,这样做会牺牲对灰度值的分辨率。
如果物体所占据的“面积”的比例是已知的,那么,通过一个简单的修正,我们的方法就会变成一个有效的方法。首先,对统计直方图求和,从而得到一个累积统计直方图。正如我们前面所提到的,累积统计直方图给出了:对于每一个灰度值,那些灰度值小于等于这个值的图像单元的数目。我们可以根据:灰度值低于某一阈值的图像单元的数目与图像单元总数的比值,来确定阈值。注意:现在,我们无法利用:根据(经过阈值化处理所得到的)二值图计算出来的面积信息。因为,在选择阈值时,我们已经“设定”了物体的面积(即:灰度值小于(或大于)我们所设置的阈值的像素点的数目)。
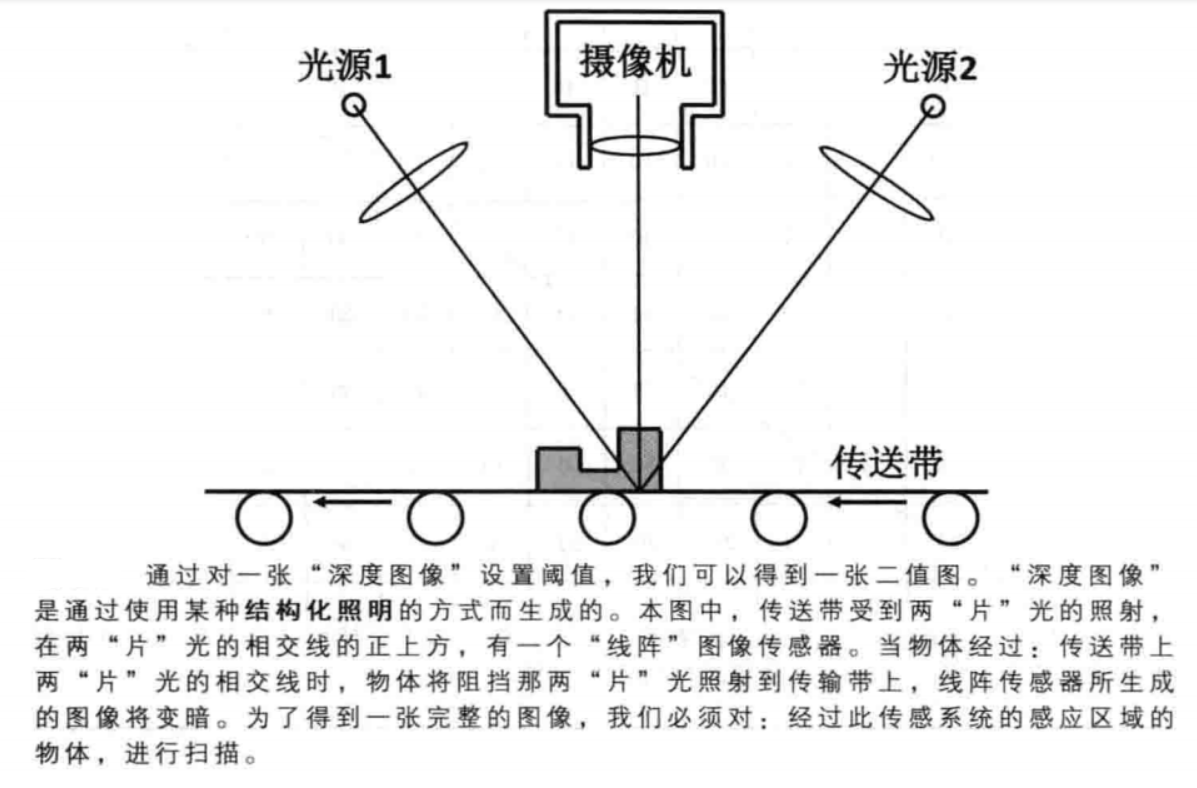
距离测量本身是可以利用光学系统来实现的,在图中,两个带有圆柱形透镜的光源所产生出的两个“光片”,相交于传送带上的一条线。我们对传送带上方的相机进行校准,从而使得:这两个“光片”的交线,在相机的感光器中的一个“线形”阵列上成像。当传送带上没有物体时,所有的感光器都得到充足的照射。当物体的一部分阻挡入射光时,“线形”阵列上的对应区域会相应地变暗。传送带不断向前移动,当物体经过传感器的感应区域时,传感器所产生的一条一条的“线”组合在一起,就形成了第二个“维度”。于是,我们最终得到了物体的轮廓。我们需要对:“光片”的宽度以及光学系统的布置,进行仔细地设计,从而使得:当传输带上下移动一小段距离时,传感器所受到的照射强度不会发生很大变化。因此,这套系统可以确定:物体的高度是否属于给定的阈值范围。
使用两个光源是为了减少“鬼影”。物体具有高度,因此,在物体达到传输带上的“那条线”之前,就会阻挡照射到“那条线”上的“光片”,从而使得感光元件所生成的图像“变黑”,这种现象被称为“鬼影”。一个未解决的问题是:如何检测物体上的深洞。系统是“看不见”深洞的。
空间相关性
对于一般的图像,图中相邻的图像单元(即:像素点)是相关的。例如,我们可以想象:在一个多面体物体的图像中,一些区域的亮度是常数。类似的,对于光滑弯曲的物体表面(所生成)的图像,随着图像中像素点位置的变化,其亮度会发生缓慢的变化。
在图像分割中,由于噪声的影响,无可避免地,一些像素点会被分错类。除了边缘附近,大部分这样的“错误”(即:像素点的错分)都是孤立的,这种“错误”被称为:椒盐噪声。在经过阈值化处理以后,通过查找和周围像素点的灰度值不一样的那些像素点,我们可以很容易地去除椒盐噪声。
在阈值化之前,通过考虑该图像单元周围像素点的灰度值,我们可以在一开始时,就避免椒盐噪声的产生。如果某一个图像单元的灰度值比它周围像素点的灰度值都高,那么,该图像单元很可能受到了“潜在的”噪声的影响。该图像单元是“异常的”,因此,我们可以将该图像单元的灰度值设置为:该点周围的像素点邻域中的最大灰度值。类似地,如果一个像素点的灰度值比它周围像素点的灰度值都要小,那么,我们也可以采用类似的“滤波”方法。注意,对于物体和背景区域的边界上的像素点,这个操作并不会改变它们的灰度值。
我们也可以使用其他的滤波方法来减少噪声。例如,我们可以通过:取该图像单元所在邻域内的所有像素点的平均灰度值,来进行滤波。但是,这个操作同时会将:图像的亮度变化“抹平”(即:减少图像和背景之间在边缘处的对比度),从而降低图像的空间分辨率。这会加剧我们在边缘处理中所碰到的问题。另外一种方式是,使用该像素邻域内所有像素点的灰度值的中位数(而不是平均数),来取代该像素点的灰度值。集合的中位数是集合中的元素,它使得:集合中小于中位数的元素个数,等于集合中大于中位数的元素个数。和第一种方法一样,这种操作不会影响到边界上的像素点。但是,相比于:求最大值或最小值(甚至求平均数),计算中位数要困难得多。
通过上面这些方法,来减少被分错类的图像单元的数目。但是,这仍然无法保障取得好的分割结果。既然在某一个图像单元上,随机噪声有时可能会产生:一个和它的期望值相差很大的灰度值,那么,在该图像单元邻域内的其他图像单元上,噪声也可能产生:一个和它的期望值相差很大的灰度值。但是,某一个图像单元的灰度值受噪声影响而产生很大的偏差的概率是较小的;同样,对于该图像单元的邻域内的其他图像单元,其灰度值受噪声影响而产生很大偏差的概率也较小。该图像单元所在邻域的灰度平均值受到噪声影响而产生很大的偏差的概率(即:这些概率的乘积)就更加小了。因此,和单个像素点比起来,邻域内像素点的灰度平均值或中位数受到噪声影响的可能性要小很多。
在这里,我们用到了像素点之间的空间相关性。到目前为止,在我们所处理的简单情况中,我们假设:物体表面具有近似一致的亮度;因此,相邻的图像单元“趋向”于:具有相同的灰度值。在这种情况下,我们通过假设:图像中应该具有什么“东西”,来引入约束条件。在后面,我们还要进一步探索和使用这种方法。
参考资料
- 伯特霍尔德・霍恩著 BERTHOLDKLAUSPAULHORN. 机器视觉[M]. 中国青年出版社, 2014.
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付