泊松编辑 （Poisson Image Editing）

图像融合在cv领域有着广泛用途，其中2003年的论文 Poisson Image Editing - 2003 因其开创性与效果拔群成为了相关领域的经典之作。而且该算法在传统图像融合算法中效果拔群，对该领域影响深远。

简介

泊松图像编辑是一种全自动的“无缝融合”两张图像的技术，由Microsoft Research UK的Patrick Perez，Michel Gangnet, and Andrew Blake在论文“Poisson Image Editing”中首次提出。

• 泊松编辑主要解决的是两个不同来源信号的无缝融合（seamless cloning）问题
• 目的是将源图像$g$的一部分内容$\Omega$融合到目标图像$f*$同样大小区域上，并使其自然融合过渡

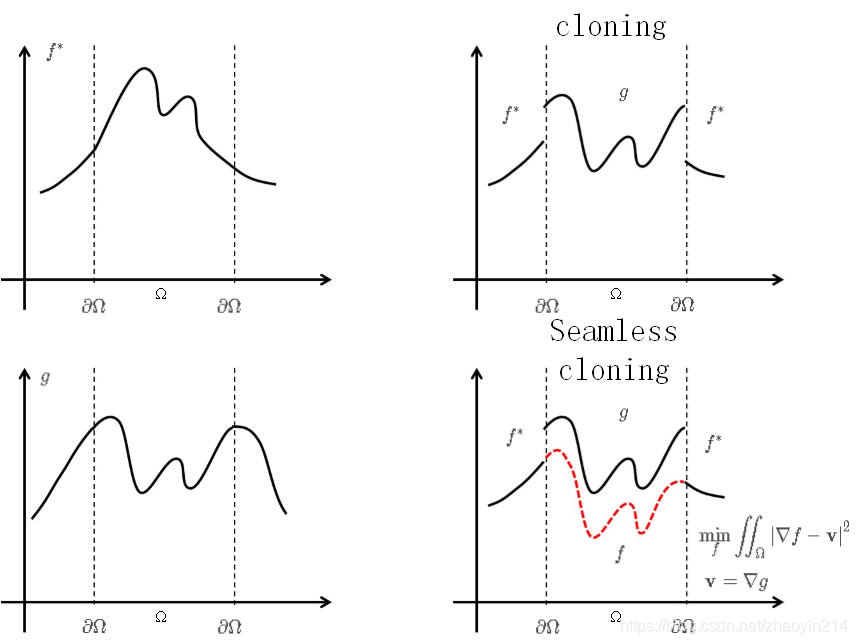
左上：目标图像$f*$，区域$\Omega$是被源图像内容替换的部分；

左下：源图像$g$，区域$\Omega$内的内容需要贴到目标图像去

右上：直接将源图像信息贴过去会有违和的边缘过渡

右下：将源的信号按照原始梯度关系变化到目标图像边界，达到了无缝融合的效果

• 泊松编辑的目标是自然地融合来源不同的图像
• 将源图像粘贴到目标图像上
• 为了保持过渡平滑，顾及了源图像粘贴区域的梯度信息与目标图像的边缘信息
• 结合已知信息求解方程组得到泊松编辑图像的结果

理论介绍

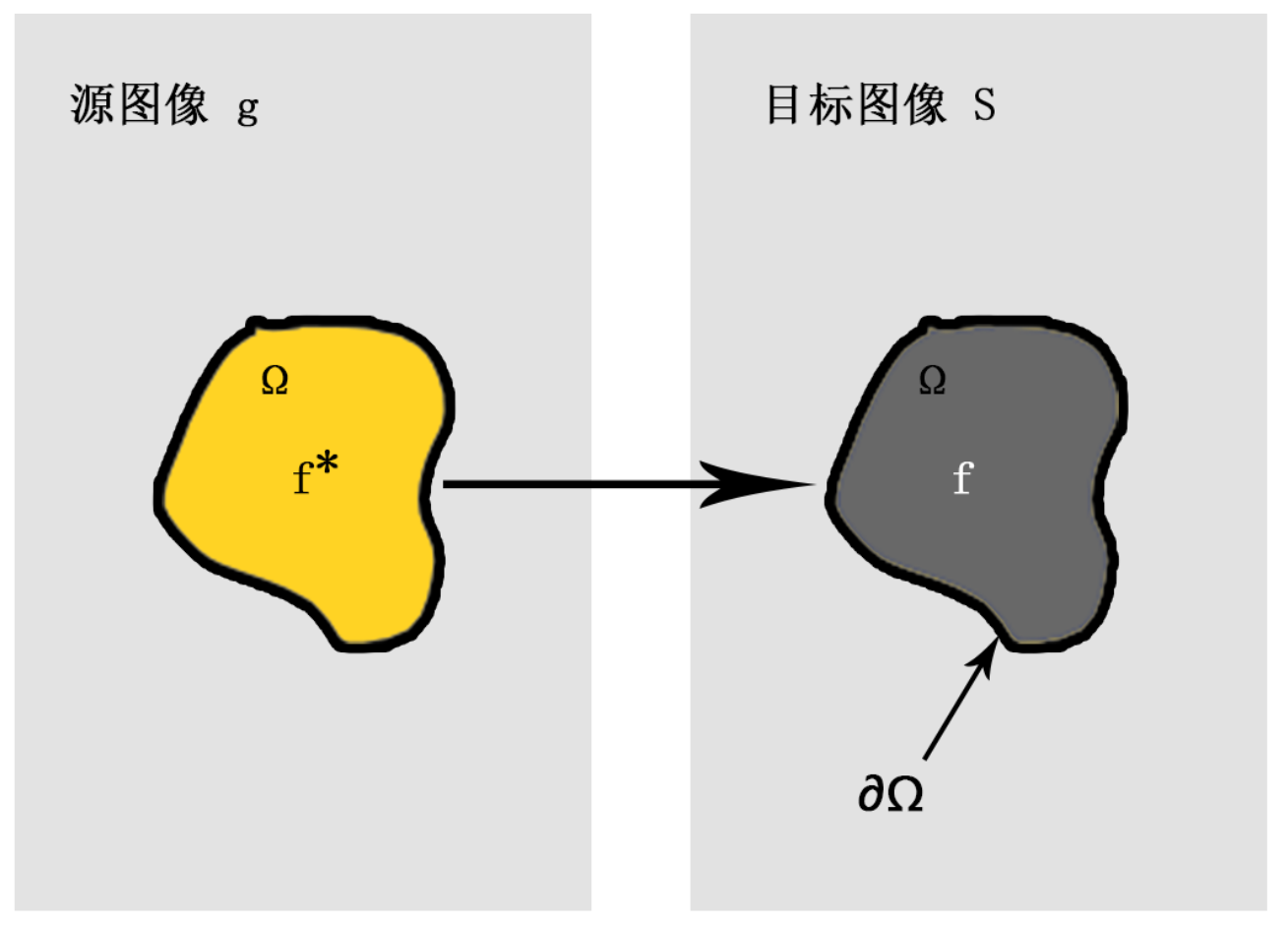
符号定义

如上图所示：

• 图像融合是要把源图像$g$的指定区域$\Omega$融合到目标图像$S$中，边缘区域为$ \partial \Omega $，源图像区域函数$f^*$，目标图像区域函数$f$。
• 这里面$g$，$\Omega$，$S$，$ \partial \Omega $，$f^*$都是已知量，需要求的是$f$

理论

泊松图像编辑的目的是保留源图像的纹理，无缝融入到新图像中。

实现的思路就是将源图像的梯度保留，应用到目标图像的边界中，解出同时满足梯度和边缘约束条件的方程，得到目标区域像素。

$$ \min _{f} \iint_{\Omega}|\nabla f-\mathbf{v}|^{2} \quad with \left.\quad f\right|_{\partial \Omega}=\left.f^{*}\right|_{\partial \Omega} $$

• $∇f$ 指的是图像函数 $f$ 的梯度

$$
\nabla .=\left[\frac{\partial_{.}}{\partial x}, \frac{\partial}{\partial y}\right]
$$

• $v$ 在原论文中是指一个引导向量场（guidance field），当用于图像合成时，它指的就是源图像的梯度。
• 这意味着上面的变分方程是指在$Ω$ 的区域内，$f$的梯度和源图像的梯度一致，而在$Ω$ 的边缘处f的值则和源图像$f^*$的值一致。这个变分方程的解是如下泊松方程在Dirichlet边界条件时的解，这也是为什么我们的融合方式叫做泊松融合。

$$ \Delta f=\operatorname{div} \mathbf{v}\text{ } over \text{ } \Omega , \text{ }with \left.f\right|_{\partial \Omega}=\left.f^{*}\right|_{\partial \Omega} $$

几个关键和符号说明

• 梯度 Gradient：

$$
\mathbf{v}=(u, v)=\nabla g
$$

• 拉普拉斯算子 Laplacian

$$ \quad \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} $$

• 散度 Divergence

$$ \begin{aligned} \operatorname{div} \mathbf{v} &=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} \\ &=\frac{\partial^{2} g}{\partial x^{2}}+\frac{\partial^{2} g}{\partial y^{2}} \\ &=\Delta g \end{aligned} $$

核心

• 也就是$f^*$和$f$的散度对应相等
• 同时保证$f^*$和$f$的边界对应相等

$$
\Delta f=\Delta f^* \text{ over } \Omega , \text{ with } \left.f\right|_{\partial \Omega}=f^{*} \mid \partial \Omega
$$

求解方程

• 将泊松方程表示为线性向量形式 $Af=b$

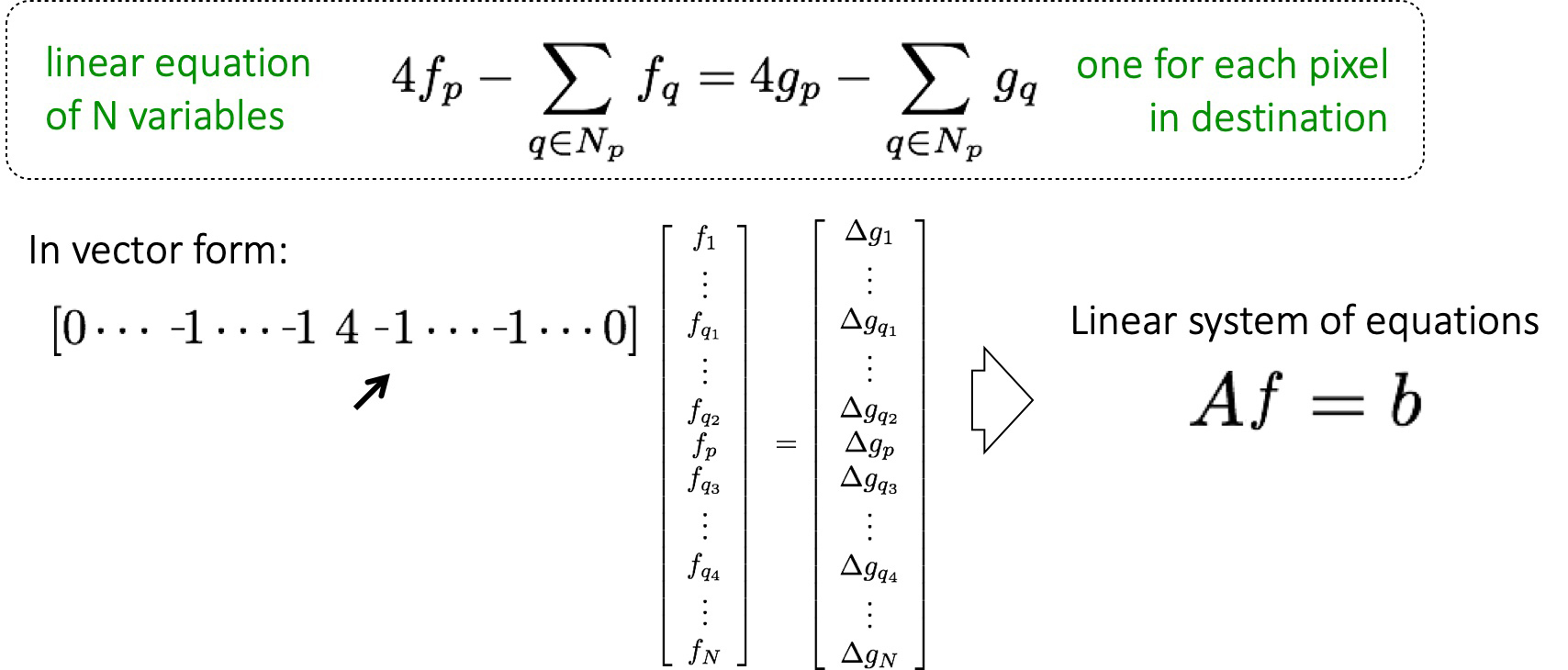
• 等号的右边是图像$g$中每一个像素的拉普拉斯滤波结果$∆gp$，这很容易理解。未知函数$f$的每个元素构成了等号左边的列向量。而系数矩阵$A$则描述了最关键的$f$的拉普拉斯滤波算子。
• 列出方程后就是解方程组了，$A$是稀疏矩阵，每行元素不超过5个，可以用 $f = b / A$计算得到

参考代码

• 参考了一份github上星星最多的泊松图像编辑代码，改成了python3并封装成类方法，供大家参考。

核心类函数为channel_process，输入图像为单通道，mask为0-1的浮点数

"""
Poisson Image Editing
William Emmanuel
wemmanuel3@gatech.edu
CS 6745 Final Project Fall 2017
"""

import numpy as np
from scipy.sparse import linalg as linalg
from scipy.sparse import lil_matrix as lil_matrix

import cv2


class Poission:
    # Helper enum
    OMEGA = 0
    DEL_OMEGA = 1
    OUTSIDE = 2

    # Determine if a given index is inside omega, on the boundary (del omega),
    # or outside the omega region
    @classmethod
    def point_location(cls, index, mask):
        if cls.in_omega(index, mask) == False:
            return cls.OUTSIDE
        if cls.edge(index, mask) == True:
            return cls.DEL_OMEGA
        return cls.OMEGA

    # Determine if a given index is either outside or inside omega
    @staticmethod
    def in_omega(index, mask):
        return mask[index] == 1

    # Deterimine if a given index is on del omega (boundary)
    @classmethod
    def edge(cls, index, mask):
        if cls.in_omega(index, mask) == False:
            return False
        for pt in cls.get_surrounding(index):
            # If the point is inside omega, and a surrounding point is not,
            # then we must be on an edge
            if cls.in_omega(pt, mask) == False:
                return True
        return False

    # Apply the Laplacian operator at a given index
    @staticmethod
    def lapl_at_index(source, index):

        i, j = index
        edge_num = 0
        minus_data = 0

        try:
            temp = source[i+1, j]
            edge_num += 1
            minus_data += temp
        except Exception as e:
            pass

        try:
            temp = source[i-1, j]
            edge_num += 1
            minus_data += temp
        except Exception as e:
            pass

        try:
            temp = source[i, j+1]
            edge_num += 1
            minus_data += temp
        except Exception as e:
            pass

        try:
            temp = source[i, j-1]
            edge_num += 1
            minus_data += temp
        except Exception as e:
            pass

        val = source[i, j] * edge_num - minus_data

        # val = (4 * source[i, j])    \
        #     - (1 * source[i+1, j]) \
        #     - (1 * source[i-1, j]) \
        #     - (1 * source[i, j+1]) \
        #     - (1 * source[i, j-1])
        return val

    # Find the indicies of omega, or where the mask is 1
    @staticmethod
    def mask_indicies(mask):
        nonzero = np.nonzero(mask)
        return nonzero[0], nonzero[1]

    # Get indicies above, below, to the left and right
    @staticmethod
    def get_surrounding(index):
        i, j = index
        return [(i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1)]

    # Create the A sparse matrix
    @classmethod
    def poisson_sparse_matrix(cls, rows, cols):
        # N = number of points in mask
        N = len(list(rows))
        A = lil_matrix((N, N))
        # Set up row for each point in mask

        points = list(zip(rows, cols))
        for i, index in enumerate(points):
            # Should have 4's diagonal
            A[i, i] = 4
            # Get all surrounding points
            for x in cls.get_surrounding(index):
                # If a surrounding point is in the mask, add -1 to index's
                # row at correct position
                if x not in points:
                    continue
                j = points.index(x)
                A[i, j] = -1
        return A

    # Main method
    # Does Poisson image editing on one channel given a source, target, and mask
    @classmethod
    def channel_process(cls, source, target, mask):
        rows, cols = cls.mask_indicies(mask)

        assert len(rows) == len(cols)
        N = len(rows)
        # Create poisson A matrix. Contains mostly 0's, some 4's and -1's
        A = cls.poisson_sparse_matrix(rows, cols)
        # Create B matrix
        b = np.zeros(N)
        points = list(zip(rows, cols))
        for i, index in enumerate(points):
            # Start with left hand side of discrete equation
            b[i] = cls.lapl_at_index(source, index)
            # If on boundry, add in target intensity
            # Creates constraint lapl source = target at boundary
            if cls.point_location(index, mask) == cls.DEL_OMEGA:
                for pt in cls.get_surrounding(index):
                    if cls.in_omega(pt, mask) == False:
                        b[i] += target[pt]

        # Solve for x, unknown intensities
        x = linalg.cg(A, b)
        # Copy target photo, make sure as int
        composite = np.copy(target).astype(int)
        # Place new intensity on target at given index
        for i, index in enumerate(points):
            composite[index] = x[0][i]

        composite = np.clip(composite, 0, 255)
        return composite.astype('uint8')

    @staticmethod
    def gray_channel_3_image(image):
        assert image.ndim == 3
        if (image[:, :, 0] == image[:, :, 1]).all() and (image[:, :, 0] == image[:, :, 2]).all():
            return True
        else:
            return False

    @staticmethod
    def image_resize(img_source, shape=None, factor=None):
        image_H, image_W = img_source.shape[:2]
        if shape is not None:
            return cv2.resize(img_source, shape)

        if factor is not None:
            resized_H = int(round(image_H * factor))
            resized_W = int(round(image_W * factor))
            return cv2.resize(img_source, [resized_W, resized_H])

        else:
            return img_source

效果示例

源图像	融合区域
目标图像	融合结果

源图像的指定区域融合到目标图像中，纵享丝滑。

参考资料

• https://github.com/willemmanuel/poisson-image-editing

• Poisson Image Editing - 2003

• https://blog.csdn.net/zhaoyin214/article/details/88196575

• https://zhuanlan.zhihu.com/p/58867397

文章链接：
https://www.zywvvd.com/notes/study/image-processing/poisson-editing/poisson-editing/