Laplace(拉普拉斯)算子

Laplace算子作为边缘检测之一，和Sobel算子一样也是工程数学中常用的一种积分变换，属于空间锐化滤波操作。

简介

• 拉普拉斯算子（Laplace Operator）是n维欧几里德空间中的一个二阶微分算子，定义为梯度（$▽f$）的散度（$▽·f$）。拉普拉斯算子也可以推广为定义在黎曼流形上的椭圆型算子，称为拉普拉斯-贝尔特拉米算子。

• 拉普拉斯算子是二阶微分线性算子，在图像边缘处理中，二阶微分的边缘定位能力更强，锐化效果更好，因此在进行图像边缘处理时，直接采用二阶微分算子而不使用一阶微分。

拉普拉斯算子

• 离散函数的导数退化成了差分，一维一阶差分公式和二阶差分公式分别为：

$$
\frac{\partial f}{\partial x}=f(x+1)-f(x)
$$
$$
\frac{\partial^{2} f}{\partial x^{2}}=f(x+1)+f(x-1)-2 f(x)
$$

• 分别对Laplace算子x,y两个方向的二阶导数进行差分就得到了离散函数的Laplace算子。在一个二维函数f(x,y)中，x,y两个方向的二阶差分分别为：

$$
\frac{\partial^{2} f}{\partial x^{2}}=f(x+1, y)+f(x-1, y)-2 f(x, y)
$$
$$
\frac{\partial^{2} f}{\partial y^{2}}=f(x, y+1)+f(x, y-1)-2 f(x, y)
$$

• Laplace算子将两个方向的差分直接累加，得到的差分形式为：

$$
\nabla^{2} f(x, y)=f(x+1, y)+f(x-1, y)+f(x, y+1)+f(x, y-1)-4 f(x, y)
$$

• 写成卷积核的形式如下：

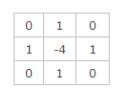
• 拉普拉斯算子符号为$ \Delta $，$ \varphi $ 是在流形上的实数或复数值的方程，它的拉普拉斯变换可表示为：

$$
\Delta \varphi
$$

源

• 另一种解释是 拉普拉斯算子其实就是针对空间标量函数的一种“操作”，即先求该标量函数的梯度场，再求梯度场的散度。
• 物理意义是求标量函数梯度场的散度。
• 求散度就可以知道空间中“源”的分布。

参考资料

• https://blog.csdn.net/hellocsz/article/details/102485387
• https://www.zhihu.com/question/26822364
• https://baike.baidu.com/item/泊松方程/251923?fr=aladdin

文章链接：
https://www.zywvvd.com/notes/study/image-processing/laplace-operator/laplace-operator/