OpenCV 畸变矫正映射

本文最后更新于：2023年12月5日下午

之前介绍了 OpenCV 完成畸变矫正的方法，本文记录直接使用矫正映射的方法。

原理

在完成图像畸变矫正获得矫正前后的相机内参，还有畸变系数之后，可以通过 OpenCV 的 initUndistortRectifyMap 函数获取映射矩阵
获取映射矩阵后可以通过 OpenCV 的 remap 函数直接对图像进行映射矫正畸变。

initUndistortRectifyMap

官方文档

函数使用：

void cv::initUndistortRectifyMap	
(	
	InputArray 	cameraMatrix,			// 输入的矫正前的相机参数（3X3矩阵）
	InputArray 	distCoeffs,				// 输入的畸变系数（5X1矩阵）
	InputArray 	R,						// 输入的第一和第二摄像头坐标系之间的旋转矩阵
	InputArray 	newCameraMatrix,		// 输入的校正后的3X3摄像机矩阵
	Size 	size,						// 摄像头采集的无失真图像尺寸
	int 	m1type,						// map1的数据类型，可以是 CV_32FC1, CV_32FC2 或 CV_16SC2
	OutputArray 	map1,				// 输出的X坐标重映射参数
	OutputArray 	map2 				// 输出的Y坐标重映射参数
)

计算方法如下：

$$ \begin{array}{c} x \leftarrow\left(u-c^{\prime}{ }_{x}\right) / f^{\prime}{ }_{x} \\ y \leftarrow\left(v-c_{y}^{\prime}\right) / f_{y}^{\prime} \\ [X Y W]^{T} \leftarrow R^{-1} *[x y 1]^{T} \\ x^{\prime} \leftarrow X / W \\ y^{\prime} \leftarrow Y / W \\ r^{2} \leftarrow x^{\prime 2}+y^{\prime 2} \\ x^{\prime \prime} \leftarrow x^{\prime} \frac{1+k_{1} r^{2}+k_{2} r^{4}+k r^{6}{ }^{6}}{1+k_{4} r^{2}+k_{5} r^{4}+k_{6 r^{6}}}+2 p_{1} x^{\prime} y^{\prime}+p_{2}\left(r^{2}+2 x^{\prime 2}\right)+s_{1} r^{2}+s_{2} r^{4} \\ y^{\prime \prime} \leftarrow y^{\prime} \frac{1+k_{1} r^{2}+k_{2} r^{4}+k r^{3} r^{6}}{1+k_{4} r^{2}+k k_{5} r^{4}+k r^{6}}+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x^{\prime} y^{\prime}+s_{3} r^{2}+s_{4} r^{4} \\ s\left[\begin{array}{c}x^{\prime \prime \prime} \\ y^{\prime \prime \prime} \\ 1\end{array}\right]=\left[\begin{array}{ccc}R_{33}\left(\tau_{x}, \tau_{y}\right) & 0 & -R_{13}\left(\left(\tau_{x}, \tau_{y}\right)\right. \\ 0 & R_{33}\left(\tau_{x}, \tau_{y}\right) & -R_{23}\left(\tau_{x}, \tau_{y}\right) \\ 0 & 0 & 1\end{array}\right] R\left(\tau_{x}, \tau_{y}\right)\left[\begin{array}{c}x^{\prime \prime} \\ y^{\prime \prime} \\ 1\end{array}\right] \\ \operatorname{map}_{x}(u, v) \leftarrow x^{\prime \prime \prime} f_{x}+c_{x} \\ \operatorname{map}_{y}(u, v) \leftarrow y^{\prime \prime \prime} f_{y}+c_{y} \\ \end{array} $$

其中 $ \left(k_{1}, k_{2}, p_{1}, p_{2}\left[, k_{3}\left[, k_{4}, k_{5}, k_{6}\left[, s_{1}, s_{2}, s_{3}, s_{4}\left[, \tau_{x}, \tau_{y}\right]\right]\right]\right]\right) $ 是失真系数。
输出的两个 map 和图像尺寸 Size 一样大。

remap

官方文档

函数使用：

void cv::remap	(	
	InputArray 	src,						// 输入图像，即原图像，需要单通道8位或者浮点类型的图像
	OutputArray dst,						// 输出图像，即目标图像，需和原图形一样的尺寸和类型
	InputArray 	map1,						// 它有两种可能表示的对象：（1）表示点（x,y）的第一个映射；（2）表示CV_16SC2，CV_32FC1等
	InputArray 	map2,						// 有两种可能表示的对象：
    										//（1）若map1表示点（x,y）时，这个参数不代表任何值；
    										//（2）表示 CV_16UC1，CV_32FC1类型的Y值
	int 	interpolation,					// 插值方式，有四中插值方式：
											//	（1）INTER_NEAREST——最近邻插值
											//	（2）INTER_LINEAR——双线性插值（默认）
											//	（3）INTER_CUBIC——双三样条插值（默认）
											//	（4）INTER_LANCZOS4——lanczos插值（默认）
	int 	borderMode = BORDER_CONSTANT,	// 边界模式，默认BORDER_CONSTANT
	const Scalar & 	borderValue = Scalar() 	// 边界颜色，默认Scalar()黑色
)

计算方法：

$$ \operatorname{dst}(x, y)=\operatorname{src}\left(\operatorname{map}_{x}(x, y), \operatorname{map}_{y}(x, y)\right) $$

示例代码

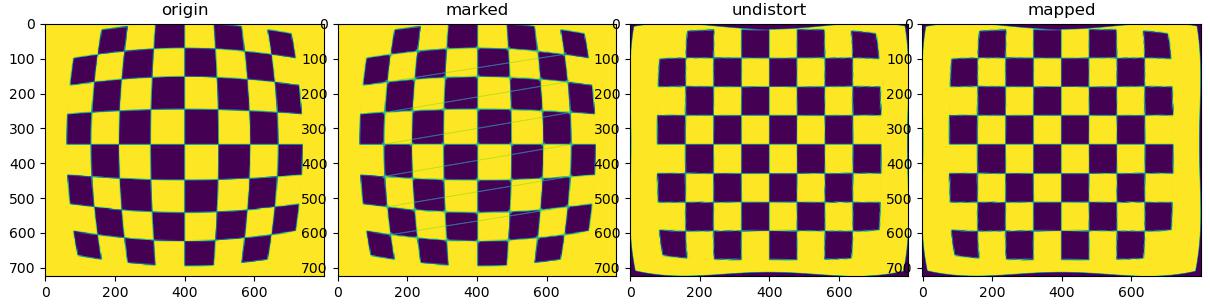
测试图像：

复用之前的代码

import numpy as np
import cv2 as cv
import mtutils as mt

# termination criteria
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,6,0)
W_num = 7
H_num = 7

objp = np.zeros((W_num*H_num,3), np.float32)
objp[:,:2] = np.mgrid[0:W_num,0:H_num].T.reshape(-1,2)

# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.

img = mt.cv_rgb_imread('undistort.png', 1)

another = img.copy()
# Find the chess board corners
ret, corners = cv.findChessboardCorners(img, (W_num,H_num), None)
# If found, add object points, image points (after refining them)
if ret == True:
    objpoints.append(objp)
    corners2 = cv.cornerSubPix(img,corners, (11,11), (-1,-1), criteria)
    imgpoints.append(corners2)
    # Draw and display the corners
    cv.drawChessboardCorners(img, (W_num, H_num), corners2, ret)
    mt.PIS(img)

ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, img.shape[::-1], None, None)
h,  w = img.shape[:2]
newcameramtx, roi = cv.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))
# 原始 mtx 效果会好一些
# dst = cv.undistort(another, mtx, dist, None, newcameramtx)
dst = cv.undistort(another, mtx, dist, None, mtx)

# 点校正
undis_corners2 = cv.undistortPoints(corners2, mtx, dist, None, mtx)

# build map matrix
# 原始 mtx 效果会好一些
# map1, map2 = cv.initUndistortRectifyMap(mtx, dist, None, newcameramtx, img.shape[::-1], cv.CV_32FC1)
map1, map2 = cv.initUndistortRectifyMap(mtx, dist, None, mtx, img.shape[::-1], cv.CV_32FC1)
frame2 = cv.remap(another2, map1, map2, cv.INTER_LINEAR)

mt.PIS([another, 'origin'], [img, 'marked'], [dst, 'undistort'], row_num=1)
pass