OpenCV 图像分析之 —— 积分图

本文最后更新于：2023年12月5日下午

积分图是一种允许子区域快速求和的数据结构，本文记录 OpenCV 图像分析中的 积分图 相关内容。

积分图

使用积分图是数字图像处理中常用的一种方法，通常能够很大程度的加速计算过程，比如均值滤波，非局部均值滤波，以及Harr计算等。

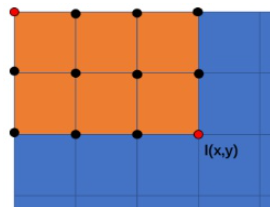
从直观来说，一张图像就是一个矩形，这个矩形中每个像素点的积分值，就是以图像左上角像素点为左上角顶点，以该像素点为右下角顶点的矩形中包含的所有元素之和。如下图所示，点(x,y)处的积分值为矩形区域中所有像素之和（包括该点）。

实际计算积分图的时候，为了提高计算效率，通常不会对每一个像素点都重新计算矩形区域包含的所有元素值之和，而是利用相邻点的积分值实现快速计算，如下图所示，点(x,y)的积分值可以使用点(x-1,y)与点(x,y-1)的积分值之和，然后减去重叠区域，也就是减去点(x-1,y-1)的积分值，最后再加上点(x,y)的像素值得到点(x,y)的积分值。

公式表示：

$$
I(x, y)=I(x-1, y)+I(x, y-1)-I(x-1, y-1)+\operatorname{pixel}(x, y)
$$

通过积分图，可以对图像的任意直立或“倾斜”的矩形区域求和、平均以及标准差。
即使目标区域大小不确定，也可以高效进行快速模糊、近似梯度、求均值以及标准差，即使对可变大小的窗口，也可执行快速块相关。

OpenCV 实现

通过 OpenCV 的cv2.integral()函数，你可以轻松地计算积分图。
OpenCV支持积分图的三种变体，分别是总和、平方求和以及倾斜求和。每种情况的结果图像在图像的每个方向上都加1之后，与原始图像的大小相同。

积分求和方式

标准积分

计算标准积分图像总和形式如下：

$$
\operatorname{sum}(x, y)=\sum_{y^{\prime}<y} \sum_{x^{\prime}<x} \operatorname{image}\left(x^{\prime}, y^{\prime}\right)
$$

平方和图像

平方和图像是平方的和：

$$ \operatorname{sum} _ { \text {square } } (x, y)=\sum_{y^{\prime} < y} \sum_{x ^ {\prime}< x} \left [\operatorname{image} \left(x ^ {\prime}, y^ {\prime} \right) \right] ^ {2} $$

倾斜求和

倾斜求和与标准求和相似，只是累加方向旋转了45度：

$$ \operatorname{sum}_{\text {tilted }}(x, y)=\sum_{y^{\prime} < y} \sum_{\operatorname{abs}\left(x^{\prime}-x\right) < y} \operatorname{image}\left(x^{\prime}, y^{\prime}\right) $$

cv2.integral()

OpenCV 执行积分图的函数

函数使用

1
2
3

cv2.integral(src[, sum[, sdepth]]) ->sum
cv2.integral2(src[, sum[, sqsum[, sdepth[, sqdepth]]]]) ->sum, sqsum
cv2.integral3(src[, sum[, sqsum[, tilted[, sdepth[, sqdepth]]]]]) ->sum, sqsum, tilted

参数说明

参数	说明
src	输入图像 $W\times H$, `uint8` 或 `float32`, `float64` 格式
sum	积分图 $(W+1)\times (H+1)$，`int32` 或 `float32` `float64` 格式
sqsum	像素平方值的积分图像 $(W+1)\times (H+1)$， `float64` 格式
tilted	对旋转了45度的图像进行积分 $(W+1)\times (H+1)$，`int32` 或 `float32` `float64` 格式
sdepth	正常图和倾斜图的积分图输出深度, `cv2.CV_32S`, `cv2.CV_32F`, 或 `cv2.CV_64F`
sqdepth	平方图的积分图输出深度，`cv2.CV_32F`, 或 `cv2.CV_64F`

示例代码

    map = np.ones([5, 5]) + 1
    sum1 = cv2.integral(map)
    sum2, sqsum2 = cv2.integral2(map)
    sum3, sqsum3, tilted = cv2.integral3(map)
    assert (sum1 == sum2).all() and (sum1 == sum3).all()
    assert (sqsum2 == sqsum3).all()


-->
map
array([[2., 2., 2., 2., 2.],
       [2., 2., 2., 2., 2.],
       [2., 2., 2., 2., 2.],
       [2., 2., 2., 2., 2.],
       [2., 2., 2., 2., 2.]])
sum1
array([[ 0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  2.,  4.,  6.,  8., 10.],
       [ 0.,  4.,  8., 12., 16., 20.],
       [ 0.,  6., 12., 18., 24., 30.],
       [ 0.,  8., 16., 24., 32., 40.],
       [ 0., 10., 20., 30., 40., 50.]])
sqsum2
array([[  0.,   0.,   0.,   0.,   0.,   0.],
       [  0.,   4.,   8.,  12.,  16.,  20.],
       [  0.,   8.,  16.,  24.,  32.,  40.],
       [  0.,  12.,  24.,  36.,  48.,  60.],
       [  0.,  16.,  32.,  48.,  64.,  80.],
       [  0.,  20.,  40.,  60.,  80., 100.]])
tilted
array([[ 0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  2.,  2.,  2.,  2.,  2.],
       [ 2.,  6.,  8.,  8.,  8.,  6.],
       [ 6., 12., 16., 18., 16., 12.],
       [12., 20., 26., 28., 26., 20.],
       [20., 30., 36., 38., 36., 30.]])