OpenCV 图像分析之 —— Canny

Canny 是1986年提出的图像边缘检测经典算法，本文记录相关内容与 OpenCV 实现。

简介

通常情况下边缘检测的目的是在保留原有图像属性的情况下，显著减少图像的数据规模。

• Canny 边缘检测算子是John F. Canny于 1986 年开发出来的一个多级边缘检测算法。更为重要的是 Canny 创立了边缘检测计算理论（Computational theory of edge detection）解释这项技术如何工作。

• Canny 的目标是找到一个最优的边缘检测算法，最优边缘检测的含义是：

  1. 最优检测：算法能够尽可能多地标识出图像中的实际边缘，漏检真实边缘的概率和误检非边缘的概率都尽可能小；

  2. 最优定位准则：检测到的边缘点的位置距离实际边缘点的位置最近，或者是由于噪声影响引起检测出的边缘偏离物体的真实边缘的程度最小；

  3. 检测点与边缘点一一对应：算子检测的边缘点与实际边缘点应该是一一对应。

• 为了满足这些要求 Canny 使用了变分法（calculus of variations），这是一种寻找优化特定功能的函数的方法。最优检测使用四个指数函数项表示，但是它非常近似于高斯函数的一阶导数。

边缘检测的三大准则

John F. 在提出Canny 的同时，提出了边缘检测的三大准则：

1. 低错误率的边缘检测：检测算法应该精确地找到图像中的尽可能多的边缘，尽可能的减少漏检和误检。
2. 最优定位：检测的边缘点应该精确地定位于边缘的中心。
3. 图像中的任意边缘应该只被标记一次，同时图像噪声不应产生伪边缘。

算法步骤

Canny边缘检测算法可以分为以下5个步骤：

应用高斯滤波平滑图像，目的是去除噪声

• 我们知道梯度算子可以用于增强图像，本质上是通过增强边缘轮廓来实现的，也就是说是可以检测到边缘的。但是，它们受噪声的影响都很大。那么，我们第一步就是想到要先去除噪声，因为噪声就是灰度变化很大的地方，所以容易被识别为伪边缘。

• 任何边缘检测算法都不可能在未经处理的原始数据上很好地工作，所以第一步是对原始数据与高斯 mask 作卷积，得到的图像与原始图像相比有些轻微的模糊（blurred）。这样，单独的一个像素噪声在经过高斯平滑的图像上变得几乎没有影响。

找寻图像的强度梯度（intensity gradients）

• 图像的边缘可以指向不同方向，因此经典Canny算法用了四个梯度算子来分别计算水平，垂直和对角线方向的梯度。但是通常都不用四个梯度算子来分别计算四个方向。常用的边缘差分算子（如Rober，Prewitt，Sobel）计算水平和垂直方向的差分Gx和Gy。这样就可以如下计算梯度模和方向：

  $$ \mathrm{G}=\sqrt{G_{x}^{2}+G_{y}^{2}} \\ \theta=\operatorname{atan} 2\left(G_{y}, G_{x}\right) $$

• 梯度角度$θ$范围从弧度$-π$到$π$，然后把它近似到四个方向，分别代表水平，垂直和两个对角线方向$(0°,45°,90°,135°)$。可以以$±iπ/8(i=1,3,5,7)$分割，落在每个区域的梯度角给一个特定值，代表四个方向之一。

• 计算图像梯度能够得到图像的边缘，因为梯度是灰度变化明显的地方，而边缘也是灰度变化明显的地方。当然这一步只能得到可能的边缘。因为灰度变化的地方可能是边缘，也可能不是边缘。这一步就有了所有可能是边缘的集合。

应用非最大抑制（non-maximum suppression）技术来消除边误检

• 通常灰度变化的地方都比较集中，将局部范围内的梯度方向上，灰度变化最大的保留下来，其它的不保留，这样可以剔除掉一大部分的点。将有多个像素宽的边缘变成一个单像素宽的边缘。即“胖边缘”变成“瘦边缘”。
• 沿着梯度方向对幅值进行非极大值抑制，而非边缘方向。
• 例如：$3\times3$区域内，边缘可以划分为垂直、水平、45°、135°4个方向，同样，梯度反向也为四个方向（与边缘方向正交）。因此为了进行非极大值，将所有可能的方向量化为4个方向，如下图：

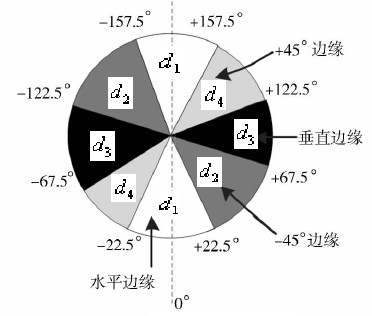
• 量化情况

边缘方向	梯度方向	角度范围
水平	垂直	$ \theta_{M} \in[0,22.5) \cup(-22.5,0] \cup(157.5,180] \cup(-180,157.5] $
135°	45°	$ \theta_{M} \in[22.5,67.5) \cup[-157.5,-112.5) $
垂直	水平	$ \theta_{M} \in[67.5,112.5] \cup[-112.5,-67.5] $
45°	135°	$ \theta_{M} \in(112.5,157.5] \cup[-67.5,-22.5] $

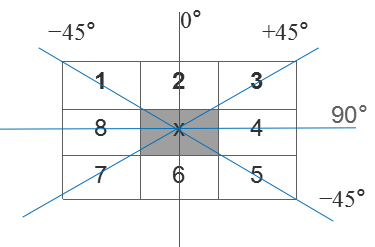
• 非极大值抑制即为沿着上述4种类型的梯度方向，比较$3\times3$邻域内对应邻域值的大小：

  • 比较当前点的梯度强度和正负梯度方向点的梯度强度。
  • 在每一点上，领域中心 x 与沿着其对应的梯度方向的两个像素相比，若中心像素为最大值，则保留，否则中心置0，这样可以抑制非极大值，保留局部梯度最大的点，以得到细化的边缘。

  

应用双阈值的方法来决定可能的（潜在的）边界

一般的边缘检测算法用一个阀值来滤除噪声或颜色变化引起的小的梯度值，而保留大的梯度值。Canny算法应用双阀值，即一个高阀值和一个低阀值来区分边缘像素。如果边缘像素点梯度值大于高阀值，则被认为是强边缘点。如果边缘梯度值小于高阀值，大于低阀值，则标记为弱边缘点。小于低阀值的点则被抑制掉。

• 选取系数TH和TL，比率为 2:1 或 3:1。（一般取TH=0.3或0.2,TL=0.1）
• 将小于低阈值的点抛弃，赋0；将大于高阈值的点立即标记为强边缘（这些点为确定边缘点）
• 将小于高阈值，大于低阈值的点标记为弱边缘

利用滞后技术来跟踪边界

至此，强边缘点可以认为是真的边缘。弱边缘点则可能是真的边缘，也可能是噪声或颜色变化引起的。为得到精确的结果，后者引起的弱边缘点应该去掉。通常认为真实边缘引起的弱边缘点和强边缘点是连通的，而又噪声引起的弱边缘点则不会。所谓的滞后边界跟踪算法检查一个弱边缘点的8连通领域像素，只要有强边缘点存在，那么这个弱边缘点被认为是真是边缘保留下来。

• 搜索所有连通的弱边缘，如果一条连通的弱边缘的任何一个点和强边缘点连通，则保留这条弱边缘，否则抑制这条弱边缘。
• 将小于高阈值，大于低阈值的点使用8连通区域确定（即：只有与TH像素连接时才会被接受，成为边缘点）

OpenCV 实现

官方文档

使用 Sobel 算子运算

• 函数使用

cv2.Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]]) ->edges

• 参数说明

参数	说明
image	uint8 格式单通道图像
edges	输出边缘图; 单通道8位图像，与图像大小相同。
threshold1	低阈值
threshold2	高阈值
apertureSize	cv2.Canny()内部调用的Sobel导数算子所用的aperturel的大小，默认为3，可选值[3, 5, 7]
L2gradient	是否使用精度高但速度慢的 $L_2$ 范数计算方向梯度，默认为 False

• 如果 L2gradient 为 True，则采用下式计算 $L_2$ 梯度：

$$ |\operatorname{grad}(x, y)|_{L_{2}}=\sqrt{\left(\frac{d I}{d x}\right)^{2}+\left(\frac{d I}{d y}\right)^{2}} $$

​ 否则使用 $L_1$ 范数计算：

$$ |\operatorname{grad}(x, y)|_{L_{1}}=\left|\frac{d I}{d x}\right|+\left|\frac{d I}{d y}\right| $$

• 实例代码

img = mt.cv_rgb_imread('img1.jpg', gray=True)
res = cv2.Canny(img, 17430, 30000, apertureSize=7)
PIS(img, res)

参考资料

• 《学习 OpenCV3》 第十二章
• https://baike.baidu.com/item/canny算法/8439208?fr=aladdin
• https://www.cnblogs.com/mightycode/p/6394810.html
• https://blog.csdn.net/weixin_40647819/article/details/91411424
• https://blog.csdn.net/saltriver/article/details/80545571
• https://www.cnblogs.com/mmmmc/p/10524640.html

文章链接：
https://www.zywvvd.com/notes/study/image-processing/opencv/opencv-canny/opencv-canny/