OpenCV 图像分析之 —— 霍夫变换(Hough Transform)

本文最后更新于：2024年5月7日下午

霍夫变换（Hough Transform）是一个关于图像领域类的一个算法，被用来检测图像中的各类曲线，直线，圆，椭圆等等，本文记录相关内容与 OpenCV 实现。

霍夫变换 (Hough Transform)

Hough（霍夫）变换是一种用于检测线、圆或者图像中其他简单形状的方法。最初Hough变换是一种线变换，这是一种相对较快的检测二值图像中直线的方法，可以进一步推广到除简单线之外的情况。

霍夫线变换

在笛卡尔坐标系下存在很多直线，直线可以用点截式表示，假设笛卡尔坐标下的两个点$A=(X_1,Y_1)$和$B=(X_2,Y_2)$：

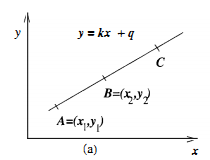
在笛卡尔坐标系下两点确定的直线为 $y=kx+q$，考虑已知的 $A,B$ 两点，则可以确定唯一的 $k,q$：

$$
\left{\begin{array}{l}q=-k x_{1}+y_{1} \ q=-k x_{2}+y_{2}\end{array}\right.
$$

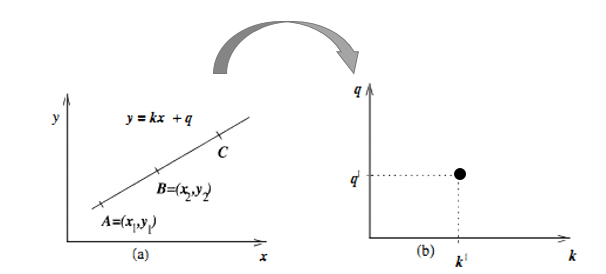
若以$k,q$为自变量、因变量可以绘制 霍夫坐标系，那么笛卡尔坐标系下的直线则对应霍夫坐标系下的一个点：

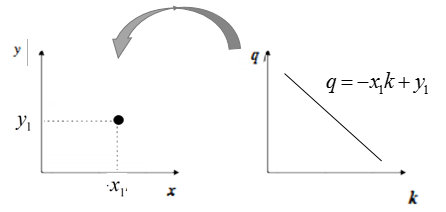
相反，考虑在笛卡尔坐标系下的一个点$(x_1,y_1)$ ，过这一点的直线方程为：

$$
q=-x_{1} k+y_{1}
$$

此时该方程表示霍夫空间下的一条直线：

当笛卡尔坐标中有两个点时,对应霍夫空间的两条直线表示:

如果有三个共线的点:

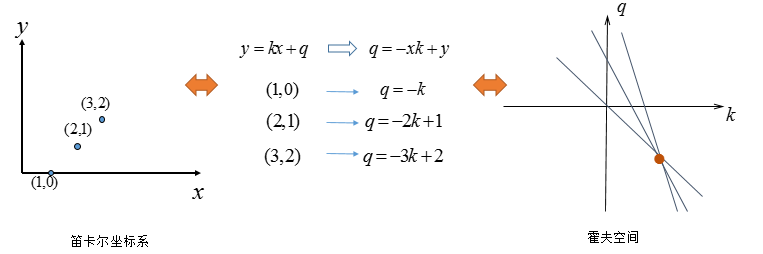
可以看到笛卡尔坐标下共线的点在霍夫空间交于一点，因为笛卡尔坐标系下的直线对应霍夫空间中的一个点
当有多个点的情况时：

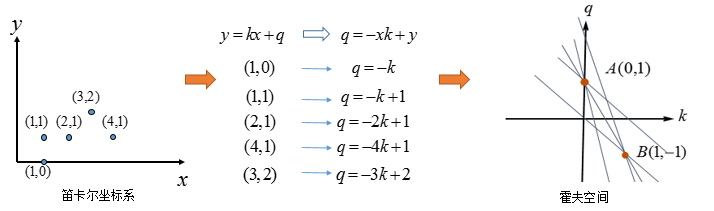
其实$(3，2)$与$(4，1)$也可以组成直线，只不过它有两个点确定，而图中A、B两点是由三条直线汇成，这也是霍夫变换的后处理的基本方式：选择由尽可能多直线汇成的点。
因此我们在霍夫空间确定$A, B$ 两个点确定的笛卡尔坐标下的直线

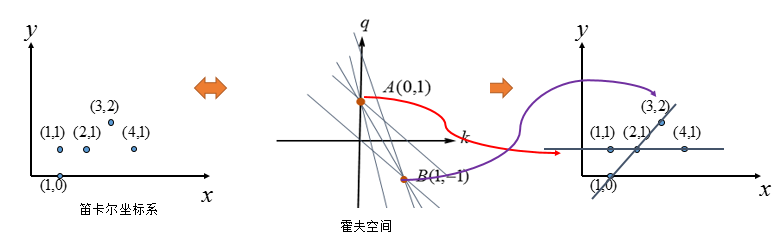
然而斜截式表示竖线是不方便的

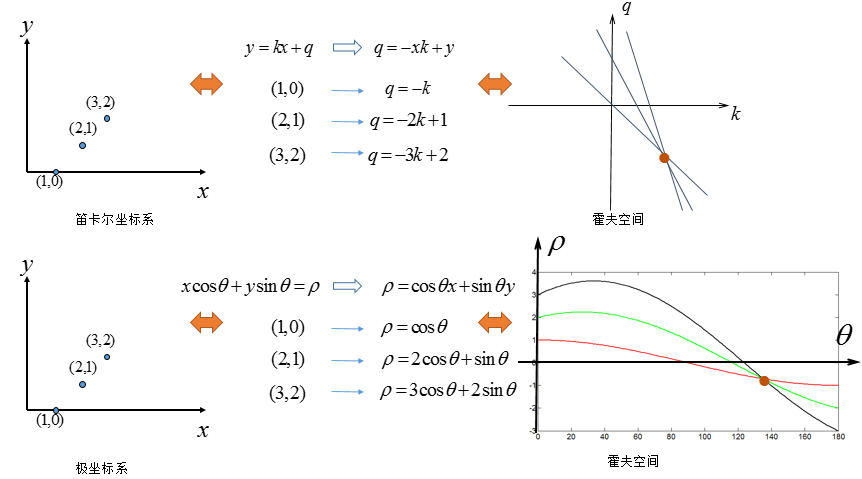
$k=∞$是不方便表示的，因此考虑将笛卡尔坐标系换为：极坐标表示。

在极坐标系下，其实是一样的：极坐标的点→霍夫空间的直线，只不过霍夫空间不再是$[k,q]$的参数，而是$ [\rho, \theta] $:

算法步骤

初始化累加器 $H$ 全零

遍历图像中的每一个边缘点

for edge point (x,y) in image:
	for theta = 0 to 180:
		rho = x * cos(theta) + y * sin(theta)
		H(round(theta), round(rho)) += 1

找到 $H$ 中局部最大值的点
将点 $(\theta, \rho)$ 转换为图像中的直线

$$
\rho=x \cos \theta+y \sin \theta
$$

cv2.HoughLines

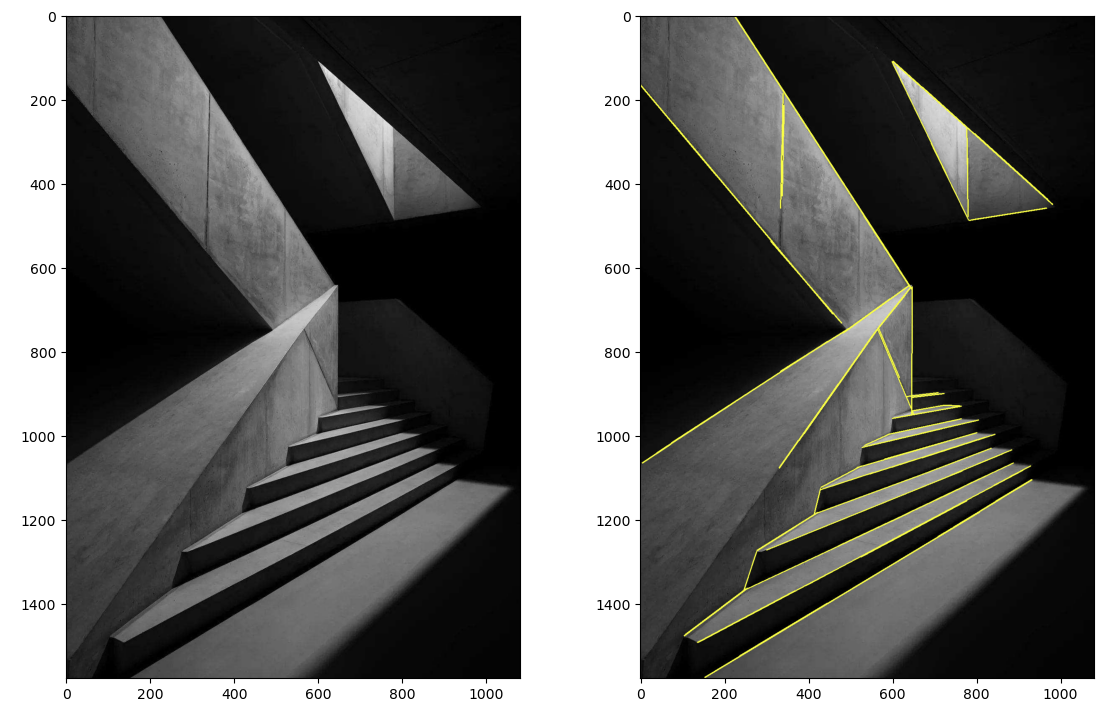
使用标准霍夫变换查找二值图像中的直线。

官方文档

函数使用

cv2.HoughLines(
	image, 				# 原图像。
	rho, 				# 累加器的距离分辨率(以像素为单位)。
	theta, 				# 累加器的弧度角分辨率。
	threshold[, 		# 累加器阈值参数。只返回那些获得足够投票的直线(> threshold)。
	lines[, 			# 返回的线，格式为 [[rho_1,theta_1], [rho_2,theta_2], ...]
	srn[, 				# 对于多尺度 Hough 变换，它是距离分辨率 ρ 的一个除数。
						  粗的累加器距离分辨率为 ρ，精确的累加器分辨率为 ρ/srn。
						  如果同时使用 srn = 0 和 stn = 0，则使用经典的 Hough 变换。
						  否则，这两个参数都应该是正数。
	stn[, 				# 对于多尺度 Hough 变换，它是距离分辨率 θ 的除数。
	min_theta[,			# 对于标准和多尺度霍夫变换，最小角度检查线。必须在0和max_theta之间。
    max_theta			# 对于标准和多尺度霍夫变换，检查线路的最大角度。必须在 min_theta 和 cv2.CV_pi 之间。
    ]]]]]) -> lines

示例代码

img = mt.cv_rgb_imread('hough_line.jpeg')
ori_img = img.copy()
gray = mt.to_gray_image(img)
edge = cv2.Canny(gray, 17430, 34000, apertureSize=7, L2gradient=True)
lines = cv2.HoughLines(edge, rho=1, theta=np.pi/180, threshold=170)

for line in lines:
    rho,theta = line[0]
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a*rho
    y0 = b*rho
    x1 = int(x0 + 1000*(-b))
    y1 = int(y0 + 1000*(a))
    x2 = int(x0 - 1000*(-b))
    y2 = int(y0 - 1000*(a))

    cv2.line(img,(x1,y1),(x2,y2),(250,250,40),2)
PIS(ori_img, img)

概率霍夫变换(Progressive Probabilistic Hough Transform)

霍夫变换用于检测直线的缺点

霍夫变换只是寻找图像中边缘像素的对齐区域，有些像素只是碰巧排成了直线，因此可能产生错误的检测结果；
可能因为多条参数相近的直线穿过了同一个像素对齐区域，而导致出现重复的结果。

算法流程

为了解决上述问题并检测到线段，可以利用概率霍夫变换解决。
概率霍夫变换算法的复杂度增加，但可以在扫描直线的过程中清除部分像素点，减少投票过程中用到的像素点。

随机获取边缘图像上的前景点，映射到极坐标系画曲线；

不是系统性地逐行扫描图像
一旦累加器的某个入口处到达了预设的最小值，就沿着对应的直线扫描图像，并移除这条直线上的所有像素点

删除点时包括还没投票的像素点
搜索边缘图像上前景点，在直线L上的点（且点与点之间距离小于maxLineGap的）连成线段，然后这些点全部删除，并且记录该线段的参数（起始点和终止点），当然线段长度要满足最小长度；

这个扫描过程还检测可以接受的线段长度。为此，算法定义两个额外的参数：一个是允许的线段最小长度，另一个是组成线段时允许的最大像素距离。
重复1. 2. 3。

cv2.HoughLinesP

用于实现概率霍夫变换寻找边缘中的直线

官方文档

函数使用

cv2.HoughLinesP(
	image, 				# 源图像。
	rho, 				# 累加器的距离分辨率(以像素为单位)。
	theta, 				# 累加器的弧度角分辨率。
	threshold[, 		# 累加器阈值参数。只返回那些获得足够投票的直线(> threshold)。
	lines[, 			# 返回线结果，格式为 [[xmin, ymin, xmax, ymax], ...]。
	minLineLength[, 	# 最短线段长度。
	maxLineGap]]]		# 点连接成线的最大距离。
	) -> lines

示例代码

img = mt.cv_rgb_imread('hough_line.jpeg')
ori_img = img.copy()
gray = mt.to_gray_image(img)
edge = cv2.Canny(gray, 17430, 34000, apertureSize=7, L2gradient=True)
lines = cv2.HoughLinesP(edge, rho=1, theta=np.pi/180, threshold=30, minLineLength=30, maxLineGap=20)
for line in lines:
    x1,y1,x2,y2 = line[0]
    cv2.line(img,(x1,y1),(x2,y2),(250,255,70),2)
PIS(ori_img, img)

霍夫圆变换

Hough圆变换的方法与之前描述的线变换方法相似。粗略解释的话，就是如果你想尝试用完全类似的方法去做，就要从累加平面变成累加三维的体积，三维坐标分别是圆心的位置x、y和圆的半径r。但这样做意味着更大的内存需求和更慢的速度。OpenCV中圆变换的实现通过采用一种称为Hough梯度法的较为复杂的方法来避免了这个问题。

理论方法

图像坐标空间中的一条已知的曲线方程也可以建立其相应的参数空间。由此，图像坐标空间中的一点，在参数空间中就可以映射为相应的轨迹曲线或者曲面。
若参数空间中对应各个间断点的曲线或者曲面能够相交，就能找到参数空间的极大值以及对应的参数；若参数空间中对应各个间断点的曲线或者曲面不能相交，则说明间断点不符合某已知曲线。
Hough变换做曲线检测时，最重要的是写出图像坐标空间到参数空间的变换公式。
对于已知的圆方程，其直角坐标的一般方程为：

$$ (x-a)^{2}+(y-b)^{2}=r^{2} $$

其中，$(a,b)$为圆心坐标，$r$为圆的半径。那么，参数空间可以表示为$(a,b,r)$，图像坐标空间中的一个圆对应参数空间中的一个点。
笛卡尔坐标空间中的一个点，对应霍夫三维空间中的一个’漏斗’。

图中可以看到笛卡尔坐标系下的圆$x^2+y2=1$ 上的三个点对应霍夫空间的三个’漏斗’：

$$ (x_i-a)^{2}+(y_i-b)^{2}=r^{2} $$

其中 $i \in { 1,2,3 }$

三个’漏斗’（取 $r > 0$ 的部分）的交点为 $(0, 0, 1)$，表明这个圆对应霍夫空间的点。

OpenCV 实现思路

Hough圆变换的方法与之前描述的线变换方法相似。粗略解释的话，就是如果你想尝试用完全类似的方法去做，就要从累加平面变成累加三维的体积，三维坐标分别是圆心的位置x、y和圆的半径r。但这样做意味着更大的内存需求和更慢的速度。OpenCV中圆变换的实现通过采用一种称为Hough梯度法的较为复杂的方法来避免了这个问题。

在用霍夫变换检测圆的实现中使用两轮筛选。
检测边缘发现可能的圆心，第一轮筛选使用一个二维累加器，找到可能的圆的位置。因为圆上像素点的梯度方向与半径方向是一致的，所以对每个像素点来说，累加器只对沿着梯度方向的入口增加计数（根据预先定义的最小和最大半径值）。
一旦检测到可能的圆心（即收到预定数量的投票），就在第二轮筛选中建立半径值范围的一维直方图。这个直方图的尖峰就是被检测圆的半径

OpenCV 霍夫圆变换

Hough梯度法工作过程如下。

首先，对图像进行边缘检测(可以使用cv2.Canny());
对每个轮廓图像中的非零点，考虑局部梯度(我们通过首先通过cv2.Sobel()计算一阶 Sobel x-导数和 y-导数来计算梯度）。

通过这个梯度，我们沿着这个斜率表示的线在累加器内从一个最小值到一个最大值遍历每个点，同时，记录轮廓图像中每个非零像素所在的位置。
然后候选圆心就从这些（二维）累加器中分离出来，这些点都高于一个阈值且同时大于其所有直接相邻的点。这些点根据其累加器值的降序排列，使得最有可能是圆心的点排在前面。
对于每个圆心，考虑所有非零像素点（之前已经构建好该列表），将这些像素根据离圆心的距离排序。从最小距离到最大半径中选择一个最好的值作为圆的半径。
如果有足够数量的点组合成一个圆并且其圆心与之前选中圆心的距离足够大，就保留这个圆心。

官方贴士：

通常该函数能很好地检测出圆的中心。但是，它可能无法找到正确的半径。您可以通过指定半径范围(minRadius 和 maxRadius)来辅助函数。或者，在 HOUGH_gradient 方法的情况下，您可以将 maxRadius 设置为一个负数，只返回中心而不进行半径搜索，并使用另一个程序找到正确的半径。

cv2.HoughCircles

OpenCV 实现霍夫圆变换的函数

官方文档

函数使用

cv2.HoughCircles(
	image, 					# 单通道灰度图像，uint8 格式
	method, 				# 检测方法，支持 cv2.HOUGH_GRADIENT 和 cv2.HOUGH_GRADIENT_ALT
							  cv2.HOUGH_GRADIENT_ALT 是 4.3.0 版本的新方法，精度较高
	dp, 					# 累加器分辨率与图像分辨率的反比
							# 例如，如果 dp=1 ，则累加器具有与输入图像相同的分辨率。
							  如果 dp=2，累加器的宽度和高度只有一半。
							# 对于 HOUGH_GRADIENT_ALT 算法，除非有很小的圆需要检测，否则建议 dp=1.5
	minDist[, 				# 检测到的圆心之间的最小距离。
							# 如果参数太小，除了一个真实的圆之外，多个相邻的圆可能会被错误地检测到。
							  如果太大，有些圆圈可能会被漏掉。
	circles[, 				# 返回的圆结果
							  如果是三维则结果为 (x, y, radius)
							  如果是四维则结果为 (x, y, radius, votes)
	param1[, 				# 第一个参数
							  对于 cv2.HOUGH_GRADIENT 和 cv2.HOUGH_GRADIENT_ALT，
							  它是传递给 Canny 算子的两个阈值中较高的阈值(较低的阈值小两倍)。
							  注意，cv2.HOUGH_ HOUGH_GRADIENT_ALT 使用 Scharr 算法计算图像导数，
							  因此阈值通常应该较高，如300或正常曝光和对比度图像。
	param2[, 				# 第二个参数
							  在 cv2.HOUGH_GRADIENT 情况下，它是检测阶段圆心的累加阈值。
							  它越小，就可能检测到越多的错误圆环。与较大的累加器值对应的“圆”将首先返回。
							  在 cv2.HOUGH_ HOUGH_GRADIENT_ALT 算法的情况下，这是圆的“完美性”度量。
							  越接近1，算法选择形状越好的圆形。在大多数情况下，0.9就可以了。
							  如果你想更好地发现小圆，你可以把它减少到0.85,0.8甚至更少。
							  但同时也要尝试限制搜索范围[ minRadius，maxRadius ] ，以避免出现许多错误的圆圈。
	minRadius[, 			# 最小的圆半径
	maxRadius]]]]]) -> 		# 最大圆半径。
							  如果该参数 <= 0，则使用最大图像维数。
							  如果该参数 < 0，当方法为 cv2.HOUGH_GRADIENT 时函数返回中心，但不找半径；
							  cv2.HOUGH_GRADIENT_ALT 总是计算圆半径。
	circles

示例代码 cv2.HOUGH_GRADIENT

img_org = mt.cv_rgb_imread('hough_circles.jpeg', gray=False)
img_org = mt.image_resize(img_org, factor=0.4)
img = mt.to_gray_image(img_org)

res = cv2.HoughCircles(img, cv2.HOUGH_GRADIENT, 1.2, 100, param1=360, param2=120, minRadius=50, maxRadius=300)
for circle in res[0]:
    x, y, radius = circle
    cv2.circle(img_org, mt.vvd_round([x, y]), mt.vvd_round(radius), color=[255, 0, 0], thickness=2)
PIS(img_org)

cv2.HOUGH_GRADIENT
- 第一，用 Sobel 导数计算局部梯度一伴随的假设是这可以被认为相当于一个局部切线一不是一个数值稳定的命题，甚至“大部分时间”都是这样，但是你应该期望在输出中产生一些噪音。
- 第二，对每个候选圆心进行判断时要考虑轮廓图像中所有非零像素。因此，如果累加器阈值过低，算法就会很慢。
- 第三，因为对每个圆心都只能选择一个圆，所以如果出现同心圆，最终将只能得到一个。最后，由于圆心根据累加器值升序排列，并且圆心距离先前被被接受的圆心太近时会被舍去，因而出现同心或近似同心圆时，算法更倾向于保留大圆。（由于Sobel导数产生的噪声，它只是一种“倾向”，但在无限分辨率下的平滑图像中，它就是必然的了。）
部分问题在新版本的算法 cv2.HOUGH_GRADIENT_ALT 中得到了改进
示例代码 cv2.HOUGH_GRADIENT_ALT

img_org = mt.cv_rgb_imread('hough_circles.jpeg', gray=False)
img_org = mt.image_resize(img_org, factor=0.4)
img = mt.to_gray_image(img_org)

res = cv2.HoughCircles(img, cv2.HOUGH_GRADIENT_ALT, 1.2, 120, param1=500, param2=0.85, minRadius=50, maxRadius=300)
for circle in res:
    x, y, radius = circle[0]
    cv2.circle(img_org, mt.vvd_round([x, y]), mt.vvd_round(radius), color=[255, 0, 0], thickness=2)
PIS(img_org)