Transformer - 1 - Self-attenstion

之前我们介绍过 Attention 的机制，但理解始终不够深刻，发现知乎一位 大神 的 Transformer 介绍，深入浅出，在此学习记录。

问题

• Attention 机制是用来做什么的 ？
• Attention 是怎么工作的？
• Self-attention 是怎么从 Attention 过度过来的 ？
• Attention 和 Self-attention 的区别是什么 ？
• Self-attention 为什么能 work ？
• 怎么用 Pytorch 实现 Self-attention ？

Attention 机制是用来做什么的

Attention 机制最早的提出是针对序列模型的，出处是 Bengio 大神在2015年的这篇文章：

https://arxiv.org/pdf/1409.0473.pdf

Bengio 大神其实是借鉴了生物在观察、学习、思考行为中的过程的一种独特的生理机制，这种机制就是 Attention 机制。大家都能有感觉，我们在获取信息的时候，通常是先从宏观上建立一个比较模糊的认识，然后又在红馆认识下，发现一些比较重要的信息，对于这些重要的信息，我们花费更多的注意力进行观察、学习和思考。

我们来看一下下面这张图，测试一下你大脑的注意力。在看图的过程中，试试回答一下，在这张图中你能看到多少张脸？

你一定发现了，当你把注意力放在不同的位置时，你能看到的脸也并不相同。这其实就是大脑的注意力机制，可以说我们无时无刻不在使用这种能力，只是我们并没有把注意力放在上面。

不同任务上，注意力的应用

机器视觉

当我们去看上面这张照片的时候，我们首先就是先去看整体，这里有车、有街道、还有很多的广告牌，不知道大家是否有感受到，当我开始描述这些的时候，其实就是我把注意力放在了这些上面了。那当我们想要跟深入了解这张图片的时候，我就要把注意力放的更聚焦。比如说，我想知道这是拍的哪里，那我可能会试着去看看广告牌上的文字 …

就像上面这张图一样，我们可能会试着把注意力放到不同的区域，那我们就能够得到更多的关于不同角度的信息。这些信息，正是我们希望在图像处理的时候希望得到的。

自然语言

自然语言处理任务中，Attention 机制表示的又是什么呢

比如说上面的这句话，“她正在吃一个绿色的苹果”，这里我们可以比较清楚的看到，“吃”和“苹果”有很强的联系，那我们就希望在处理吃这个单词的时候，能够在语义中，包含一定的苹果的信息，这样能够帮助我们更好的理解“吃”这个动作。“绿色的”和“苹果”也是一样的，Attention的机制能够帮助我们在处理单个的 token 的时候，带有一定的上下文信息。这就像是一种“软性记忆”一样，帮助我们记住上下文中包含的信息。

当我们看一篇文章的时候，其实也是类似的。我们从拿到一篇文章开始，首先关注的也只是一些关键性的词语，这些关键性的词语，就能够帮助我们快速的判断文章的内容和结构。这些场景就是我们在一些具体场景中对 Attention 的应用。

推荐系统

通常来说，我们构建的推荐系统是通过对于用户历史行为、用户特征、物品特征等的观测，来判断用户是否会对一个新的物品感兴趣。

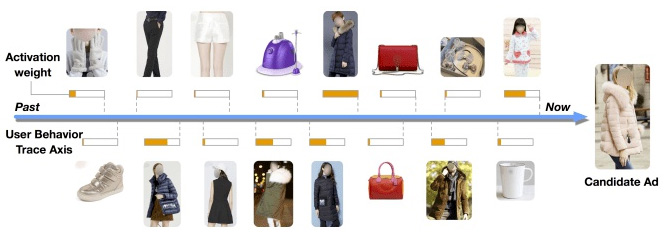
就像上图中一样，从左到右表示用户从过去到现在所购买的商品序列，现在就是要通过观察这些序列、用户特征、商品特征，来判断新出现的一个商品，用户会不会购买。

但是，再这样的一个判断的过程中，我们会发现，购买序列中的某一些商品对于当前的这个商品购买是具有局定性的指导作用的，而其他的商品可能就没那么的重要。比如说，我购买了手套、靴子，就对我可能会购买羽绒服的决定比我买手机、键盘要更重要一些。这个重要性，就是我们希望能够从购买序列中发现的，他能帮着我们更好的判断新商品购买的可能性。

这个重要性其实就是注意力！我们的模型在去做判断的时候，到底应该把哪些物品当成是重要的判断依据，这能大大的提高我们模型的准确性。

Attention 是怎么工作的

其实总结下来，Attention 机制的工作原理并不复杂，我可以用下面这张图做一个总结。

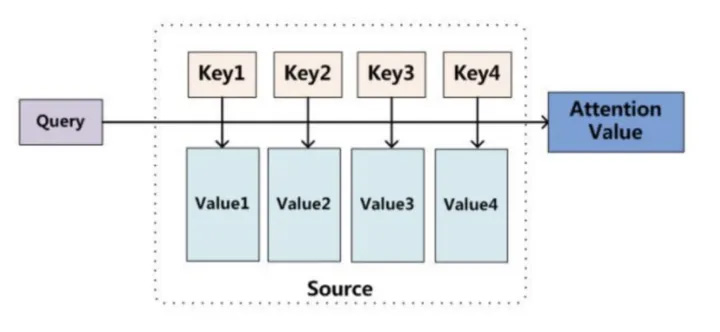
一个 Attention 的计算过程有三步：

• query 和 key 进行相似度计算，得到一个 query 和 key 相关性的分值；
• 将这个分值进行归一化(softmax)，得到一个注意力的分布；
• 使用注意力分布和 value 进行计算，得到一个融合注意力的更好的 value 值。

在原始论文中三步走怎么做的

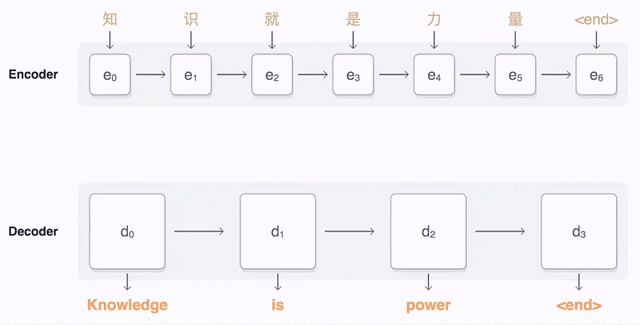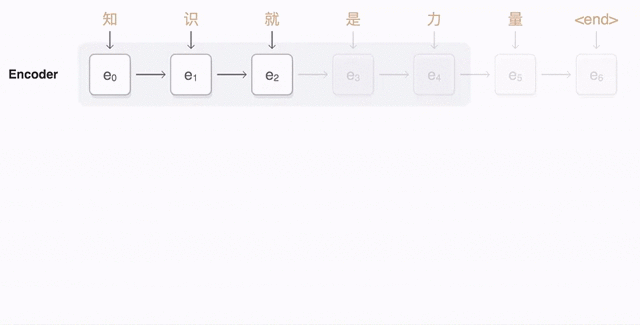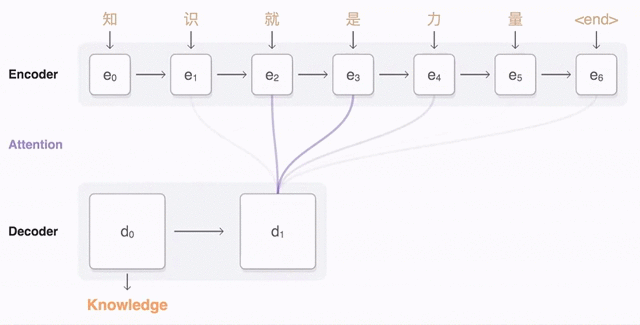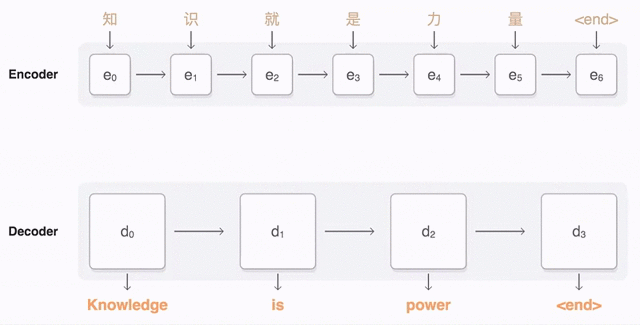
为了更好的说明上面的这个过程，我们可以看看在 Bengio 提出注意力的这篇论文中，以上这三步分别是什么。Bengio 在原文中是想通过注意力来做一个机器翻译(NMT) 的任务，机器翻译中，我们会使用 seq2seq 的架构，每个时间步从词典里生成一个翻译的结果。就像下面这张图一样。

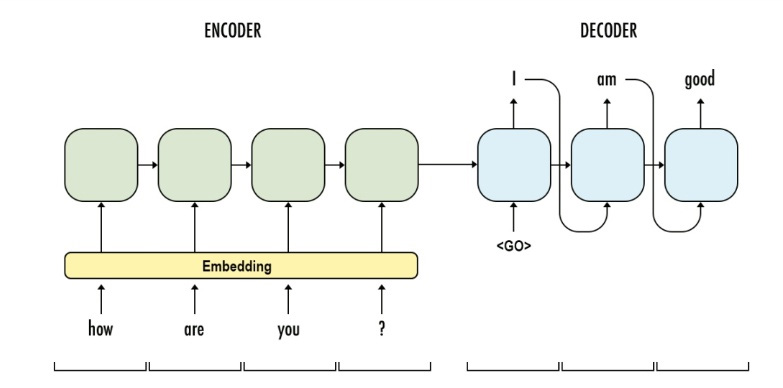
在没有注意力之前，我们每次都是根据 Encoder 部分的输出结果来进行生成，提出注意力后，就是想在生成翻译结果时并不是看 Encoder 中所有的输出结果，而是先来看看，我想生成的这部分和哪些单词可能关系会比较大，关系大的我多借鉴些；关系小的，少借鉴些。就是这样一个想法，我们看看该如何操作。

• 这里为了生成单词，我们把 Decoder 部分输入后得到的向量作为 query；把 Encoder 部分每个单词的向量作为 key。我先我们先把 query 和每一个单词进行点乘 $score = query \cdot key$，得到相关性的分值；
• 有了这些分值后，我们对这些分值做一个 softmax ，得到一个注意力的分布；
• 有了这个注意力，我们就可以用它和 Encoder 的输出值 (value) 进行相乘，得到一个加权求和后的值，这个值就包含注意力的表示，我们用它来预测要生成的词。

在推荐系统中三步走怎么做的

在商品推荐系统中，query 就是我当前要判断的商品的向量，key 就是用户购买序列中，每一个商品的向量。

• query 和 key 进行相似度计算，得到待判断商品和购买序列中商品的相关性分值；
• 将这个分值进行归一化(softmax)，得到一个商品注意力的分布，看看哪些商品是判断的重要依据；
• 使用注意力分布和 value 进行计算，得到一个融合注意力的更好的 value 值，这个值就是最终我们融合判断当前商品是否推荐购买的依据。

当然，Attention 并不是只有这一种计算方式，后来还有很多人找到了各种各样的计算注意力的方法。但是从本质上，它们都遵循着这个三步走的逻辑，如果你能把对它的理解，放到你的任务中，那你就离着创造自己的 Attention 不远了。

• query 和 key 进行相似度计算，得到一个 query 和 key 相关性的分值；
• 将这个分值进行归一化(softmax)，得到一个注意力的分布；
• 使用注意力分布和 value 进行计算，得到一个融合注意力的更好的 value 值。

如果能够理解 Attention 了，那么接下来，我们来看看 Self-attention 是怎么衍生出来的。

Self-attention 是怎么从 Attention 衍生出来的过来的

Self-attention 就本质上是依然是一种特殊的 Attention，是在 Transformer 中最重要的结构之一。

上面我们介绍了 Attention 机制，它能够帮我们找到子序列和全局的相关度的关系，也就是找到权重值 $w_i$ 。Self-attention 对于 Attention 的变化，其实就是寻找权重值 $w_i$ 的过程不同。原来，我们计算 $w_i$ 时使用的是子序列和全局，而现在我们计算 Self-attention 时，用的是自己和自己，这是 Attention 和 Self-attention 从计算上来说最大的区别。

接下来，我们来看看 Self-attention 的运算过程。为了能够产生输出的向量 $y_i$ ，Self-attention 其实是对所有的输入做了一个加权平均的操作，这个公式和上面的 Attention 是一致的。
$$
y_{i}=\sum_{j} w_{i j} x_{j}
$$
$ j $ 代表整个序列的长度，并且 $ j $ 个权重的相加之和等于 1 。值得一提的是，这里的 $ w_{i j} $ 并不是一个 需要神经网络学习的参数，它是来源于 $ x_{i} $和 $ x_{j} $ （这里 $ x_{i} $和 $ x_{j} $ 就都是自己 self）的之间的计算的结果。而它们之间最简单的一种计算方式，就是使用点积的方式。

$$ w_{i j}^{\prime}=\boldsymbol{x}_{i}^{\top} \boldsymbol{x}_{j} $$

这个点积的输出的取值范围在负无穷和正无穷之间，所以我们要使用一个 Softmax 把它映射到 [0,1] 之间，并且要确保它们对于整个序列而言的和为 1。

$$ w_{i j}=\frac{\exp w_{i j}^{\prime}}{\sum_{j} \exp w_{i j}^{\prime}} $$

以上这些就是 Self-attention 最基本的操作。

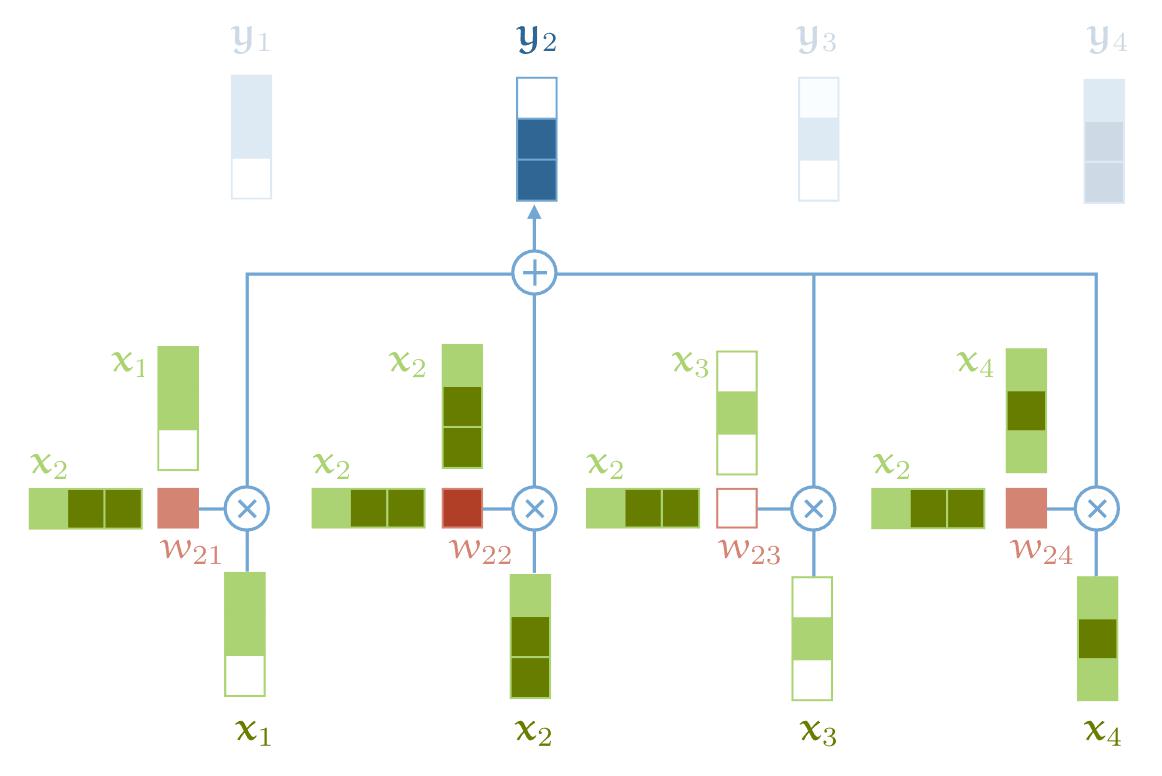
图中没有画出 softmax，事实上是有的

Attention 和 Self-attention 的区别是什么

这里有几个重要的区别，可以帮助大家更好的区分在不同任务中的使用方法：

1. 在神经网络中，通常来说你会有输入层（Input），应用激活函数后的输出层（Output），在 RNN 当中你会有状态（State）。如果 Attention (AT) 被应用在某一层的话，它更多的是被应用在输出或者是状态层上，而当我们使用 Self-attention（SA），这种注意力的机制更多的是在关注 Input 自己身上。
2. SA 可以在一个模型当中被多次的、独立的使用（比如说在Transformer中，使用了18次；在Bert当中使用12次）。但是，AT在一个模型当中经常只是被使用一次，并且起到连接两个组件的作用。两个不同的组件（Component），编码器和解码器。但是如果我们用 SA，它就不是关注的两个组件，它只是在关注你应用的那一个组件。那这里他就不会去关注解码器了，就比如说在 Bert 中，使用的情况，我们就没有解码器。
3. SA 比较擅长在一个序列当中，寻找不同部分之间的关系。比如说，在词法分析的过程中，能够帮助去理解不同词之间的关系。AT 却更擅长寻找两个序列之间的关系，比如说在翻译任务当中，原始的文本和翻译后的文本。这里也要注意，在翻译任务中，SA 也很擅长，比如说 Transformer。
4. AT 可以连接两种不同的模态，比如说图片和文字。SA 更多的是被应用在同一种模态上，但是如果一定要使用SA来做的话，也可以将不同的模态组合成一个序列，再使用 SA。
5. 对我来说，大部分情况，SA 这种结构更加的 general，在很多任务作为降维、特征表示、特征交叉等功能尝试着应用，很多时候效果都不错。

Self-attention 为什么能 work

上面描述的方法看起来似乎很简单，但是它为什么能够 work 呢？为了能够建立起直观的感受，让我们来看看一种标准的推荐电影的方法，看看是否能得到一些启发。

假设你正在运营一家在线看电影的网站，你有一些电影和一些用户，你想要把合适的电影推荐给你的用户。你该怎么办呢？

推荐中的解释

一种方法是这样的，给你的电影手动的创建一些特征(feature)，比如说这部电影关于爱情的部分有多少，关于动作的部分有多少；然后我们再去对用户的特征进行分析，比如说用户 A 对于爱情电影的喜爱程度有多少，对动作电影的喜爱程度有多少。如果我们按照上述方式构建了用户和电影的两个矩阵，那么它们的点积就会给你一个分数，这个分数就代表了用户对于某种电影的喜爱程度。

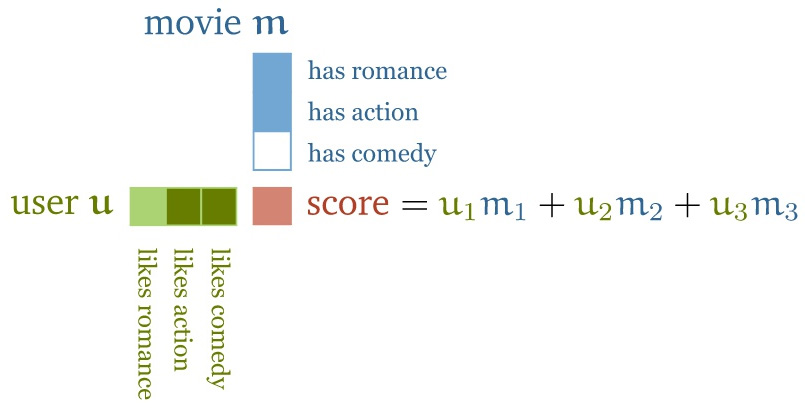
通过上面的这种计算方式，我们就能够得到一些 Score 值。这些值有正数也有负数。比如说，电影是一部关于爱情的电影，并且用户也很喜欢爱情电影，那么这个分值就是一个正数；如果电影是关于爱情的，但是用户却不喜欢爱情电影，那么这个分值就会是一个负值。

还有，这个分值的大小也表示了在某个属性上，它的程度是多大：比如说某一部电影，可能它的内容中只有一点点是关于爱情的，那么它的这个值就会很小；或者说有个用户他不是很喜欢爱情电影，那么这个值的绝对值就会很大，说明他对这种电影的偏见是很大的。

显而易见，上面说的这种方法在现实中是很难实现的。我们很难去人工标注上千万的电影的特征，和用户喜欢哪种类型的电影的分值。

那么，我们有没有一种方法去通过问一小部分人，通过收集他们对电影的喜好，来通过一些算法来优化找出用户对于电影喜爱程度这个模型的参数呢？当然是有的，那就是 FM 算法，Factorization Machine。这个算法就是能通过左边的这个用户-电影矩阵，找到用户对于不同特征的喜好程度。

上面右边的矩阵是怎么来的呢？我们把上面的这个问题简化一下，只看成是一个和用户、物品两个维度相关的任务，那其实我们就可以通过估计两个矩阵的点乘，来对原有的矩阵进行计算。

这两个向量中表示的就分别是用户的 Embedding 和电影的 Embedding。我们反过来思考下，这种办法的核心思想就是是通过两个低维小矩阵（一个代表用户 Embedding 矩阵，一个代表物品 Embedding 矩阵）的点乘计算，来模拟真实用户点击或评分产生的大的协同信息稀疏矩阵，本质上是编码了用户和物品协同信息的降维模型。

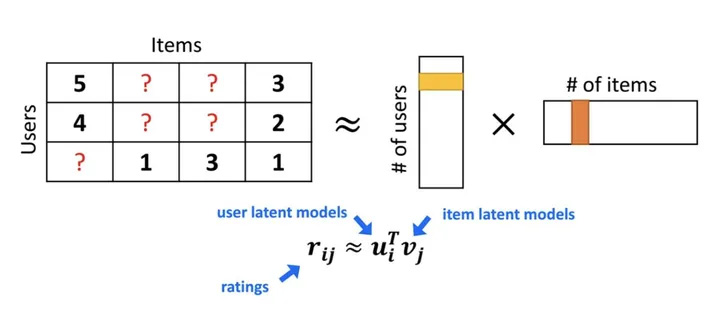
当我们想要看，某个用户对于某个电影的喜好程度时，只需要用他们的 Embedding 相乘，就能得到相应的 Score了。

上面的这个过程，就和我们使用下面这个公式来表示 Attention 的想法是一致的。

$$ \boldsymbol{w}_{i j}^{\prime}=\boldsymbol{x}_{i}^{\top} \boldsymbol{x}_{j} $$

自然语言处理中的解释

那再让我们看一个在自然语言处理中使用 Self-attention 的例子。为了应用 Self-attention，我们给每一个在词表中的单词 t 一个 Embeding 向量 $v_t$ (这个是我们通过一些 NLP 方法学习到的)。这也是我们在序列模型中常见的 Embeding Layer。它会把单词 the,cat,walks,on,the,street 转换成向量的形式

$$ \boldsymbol{v}_{\text {the }}, \boldsymbol{v}_{\text {cat }}, \boldsymbol{v}_{\text {walks }}, \boldsymbol{v}_{\text {on }}, \boldsymbol{v}_{\text {the }}, \boldsymbol{v}_{\text {street }} $$

如果我们对这些向量序列进行 Self-attention的处理，那么就会生成一个新的向量序列:

$$ \mathbf{y}_{\text {the }}, \mathbf{y}_{\text {cat }}, \mathbf{y}_{\text {walks }}, \mathbf{y}_{\text {on }}, \mathbf{y}_{\text {the }}, \mathbf{y}_{\text {street }} $$

这其中 $ y_{c a t} $ 就是所有在第一个序列中的 Embedding 向量的加权和，权重值就是 $ v_{c a t} $ 的点积。

上文中我们也提到了， $ v_{t} $ 是我们学习到的 Embedding 向量，它是 $ t $ 这个单词向量化的表示。在 大部分的场景中， the 这个单词和句子中的其他单词没有很强的相关性，因此，我们就会期待 $ v_{\text {the }} $ 和其他单词的点积结果应该比较小或者是一个负值。那再看 walks ​ 这个单词，为了能够解释这个单词，我们希望能够知道是谁在 walk ，那在这句话当中， $ v_{\text {cat }} $ 和 $ v_{\text {walks }} $ 的点积就应该有一个比较大的正的值。

以上这些，就是在 Self-attention 背后一些直觉上的含义。点积操作很好的表示了输入语句中两个向量之间的相关性。

在我们继续下面的内容之前，非常有必要做一个小的总结。

• 到目前为止，我们还没有用到需要学习的参数。基础的 Self-attention 实际上完全取决于我们创建的输入序列，上游的 Embeding Layer 驱动着 Self-attention 学习对于文本语义的向量表示。
• Self-attention看到的序列只是一个集合(set)，不是一个序列，它并没有顺序。如果我们重新排列集合，输出的序列也是一样的。后面我们要使用一些方法来缓和这种没有顺序所带来的信息的缺失。但是值得一提的是，Self-attention 本身是忽略序列的自然输入顺序的。
• 再来一个动画，看看self-attention的过程。

怎么用 Pytorch 实现 Self-attention

我们将一起从头开始写一个 Self-attention。我们这里将会使用 Pytorch 来实现。

一个简单的实现方法就是循环所有的向量，去计算出权重和输出，但是这样的方法明显太慢了。所以我们要做的第一件事就是怎么使用矩阵乘法的形式来表达 Self-attention。

我们首先来表示输入，一个 $ k $ 维的由 $ t $ 个向量组成的序列构成的矩阵 $ X $ 。包含一个 batch 的参 数 $ b $ ，我们会得倒一个维度为 $ (b, t, k) $ 的张量。

所有的点积的结果 $ w_{i j}^{\prime} $ 也构成一个矩阵，我们可以简单的使用 $ X $ 乘以它的转置得到。

import torch
import torch.nn.functional as F

# assume we have some tensor x with size (b, t, k)
x = ...

raw_weights = torch.bmm(x, x.transpose(1, 2))
# - torch.bmm is a batched matrix multiplication. It 
#   applies matrix multiplication over batches of 
#   matrices.

然后我们把权重值 $ w_{i j} $ 转换成正值并且确保它们的和为 1 ，我们使用一个 row-wise 的 Softmax。

weights = F.softmax(raw_weights, dim=2)

最后，我们计算输出的序列，我们只需要使用权重 $ w_{i j} $ 乘以矩阵 $ X $ 。这样我们就得到了维度为 $ (b, t, k) $ 的矩阵 $ Y $ 。

y = torch.bmm(weights, x)

以上，经过两个简单的矩阵乘法和一个 softmax，我们就得到了 self-attention。

参考资料

• https://zhuanlan.zhihu.com/p/345680792
• https://peterbloem.nl/blog/transformers
• https://www.zywvvd.com/notes/study/deep-learning/attention/attention/
• https://www.zhihu.com/people/CYang

文章链接：
https://www.zywvvd.com/notes/study/deep-learning/transformer/transformer-intr/transformer-intr-1/