本文最后更新于：2024年5月7日 下午

本文继续 大神 的 Transformer 介绍，进入第二篇 —— Transformer 中的 SA。

问题

上一篇中，我们有说到 Self-attention 其实是 Attention 的一个变体，改变了计算相关性权重的计算方式，从输出和输入之间的相关计算，转变成输入和输入自身的相关性计算。

本篇是对上一篇的继续，Transformer 的作者基于 Self-attention 存在的局限性，针对性的做出了相应的 tricks，加以提升 Self-attention 的拟合数据的能力。

本文重点解决以下问题：

  • Transformer 的作者对基础的 Self-attention 做了哪些 tricks ？
  • 怎么用 Pytorch/Tensorflow2.0 从头实现在 Transfomer 中的 Self-attention ？

Transformer 的作者对 Self-attention 做了哪些 tricks

在 Transformer 的实现过程中，作者使用了三个 tricks。

Queries, keys and values

我们再来回顾一下上面所说道的 Self-attention 的内容，上面我们也提到了，在这样一个模型当中，是没有使用到可以学习参数的，那我们能不能使用一些参数，来让整个结构更加的 flexable。就是由于这样的想法，诞生了query，key 和 value 这些参数。

为了能够更清楚的说明，我们使用图片来稍微回顾下，之前讲过的 Self-attention。

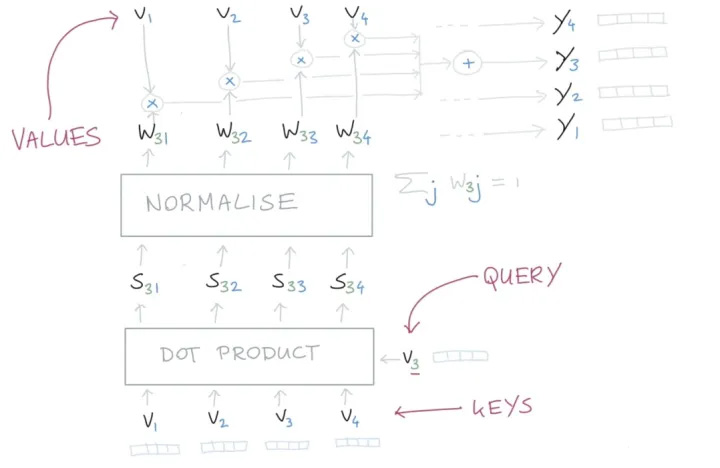
在整个计算的过程中，大家会发现，我们使用了三次向量 $ v_{i} $ 这个文本的表示来做计算，那在 Transformer 中，就是把这几个变量参数化，使用可以学习的参数来替代，这里我们分别使用 key、query 和 value 三个可学习的向量来表示，这里记为 $ W_{q} ， W_{k} ， W_{v} $ ，通过下面的计算，来得到一个使用注意力机制重新计算后的向量 $ y $ 。

$$ \mathbf{q}_{i}=\mathbf{W}_{\mathbf{q}} \boldsymbol{x}_{\mathrm{i}} \quad \mathbf{k}_{\mathrm{i}}=\mathbf{W}_{\mathrm{k}} \boldsymbol{x}_{\mathrm{i}} \quad \boldsymbol{v}_{\mathrm{i}}=\mathbf{W}_{v} \boldsymbol{x}_{\mathrm{i}} $$ $$ \begin{aligned} w_{i j}^{\prime} & =\mathbf{q}_{i}^{\top} \boldsymbol{k}_{j} \\ w_{i j} & =\operatorname{softmax}\left(w_{i j}^{\prime}\right) \\ \mathbf{y}_{i} & =\sum_{j} w_{i j} \boldsymbol{v}_{j}\end{aligned} $$

这里面 key，query，value 分别学习到的是什么呢？这个可能并没有一个官方的解释，但是通过这三个名称的命名方式，我们可以大致的猜测。

这种命名的方式来源于搜索领域，假设我们有一个 key-value 形式的数据集，就比如说是我们知乎的文章，key 就是文章的标题，value 就是我们文章的内容，那这个搜索系统就是希望，能够在我们输入一个 query 的时候，能够唯一返回一篇最我们最想要的文章。那在 Self-attention 中其实是对这个 task 做了一些退化的处理，我们优化并不是返回一篇文章，而是返回所有的文章 value，并且使用 key 和 query 计算出来的相关权重，来找到一篇得分最高的文章。

缩放点积的值(Scaling the dot product)

Softmax 函数对非常大的输入很敏感。这会使得梯度的传播出现为问题(kill the gradient)，并且会导致学习的速度下降(slow down learning)，甚至会导致学习的停止。那如果我们使用 $ \sqrt{k} $ 来对输入的向量做缩放，就能够防止进入到 Softmax 函数的饱和区，使梯度过小：

$$ \boldsymbol{w}_{i j}^{\prime}=\frac{\mathbf{q}_{i}^{\top} \mathbf{k}_{j}}{\sqrt{k}} $$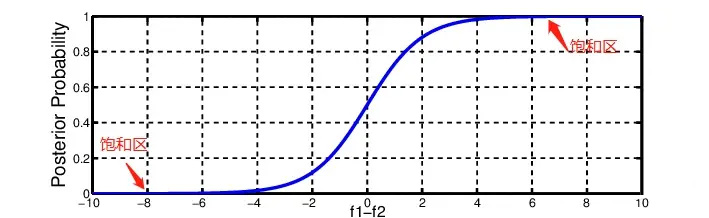

这里分母为什么要使用 $ \sqrt{k} $ 呢？我们想象一下，当我们有一个所有的值都为 $c$ 的在 $ℜ_k$ 空间内 的值。那它的欧式距离就为 $ \sqrt{k} c $ 。除以 $ \sqrt{k} $ 其实就是在除以向量平均的增长长度。

Multi-head attention

最后，我们必须要知道的是，在真实的语言环境中，每一个词和不同的词，都有不同的关系。我们考虑下面这个例子，I gave my dog Charlie some food。我们可以看到 gave 和不同的部分有不同的关系。首先，I 表示谁在进行 give 的动作，food 表达被 give 的东西是什么，Charlie 表示准在接受东西。我们就可以用不同的Self-attention来捕获这些不同的关系。如下图：

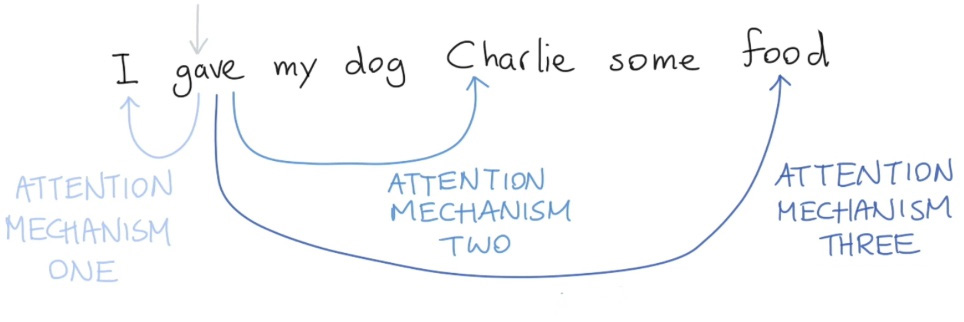
如果我们只进行一个 Self-attention, 所有的信息都会被加和到一起。如果是 Charlie 给 I food,那么我们得到的 $y_{gave}$ 就是一样的了，但是其实意思应发生了改变。

所以，我们可以通过增加多个 Self-attention 这样的结构，来给 self attention 更强的辨别能力， 我们就有了更多个$q,k,v$的矩阵 $W_q^r,W_k^r,W_v^r$ , 那我们把这些不同的 Self-attention 就叫做 Attention Head。

有了多个 Self-attention 所代表的不同的参数，我们就可以用来表示不同的词之间的不同层面的关系了，比如说，语义层面的信息、词法方面的信息、时态方面的信息等等，这就大大的加强了 Self-attention 捕获信息的能力。

对于输入 $ x_{i} $ 每一个 Attention Head 都会生成一个向量 $ y_{i}^{r} $ 。我们把这些向量进行 concat 操作，并且把 concat 的结果传递给一个全连接层，使得向量的维度重新回到 $k$。这样我们就得到了一个表示能力更强的向量。应用了multi-head 后的 Self-attention 计算过程就变成了下图这样子：

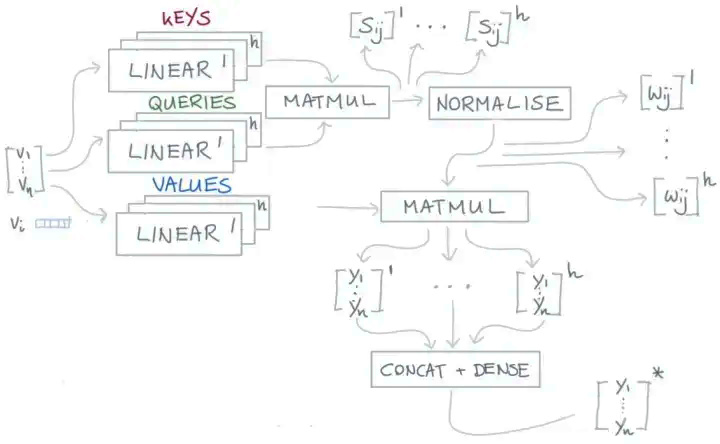
我们可以看到，上图中大部分的计算过程和单一 Self-attention 计算过程是一致的。只是在使用 Linear 层时，我们使用多个 Linear 层，这就相当于是增加了多组的可学习参数，这些可学习参数就是我们上文中说到的能够学习到不同层次关系的参数。

有了这个结构，我们就可以把多个 Multi-head Attention 结构堆叠起来，从而得到更加强大的能力。

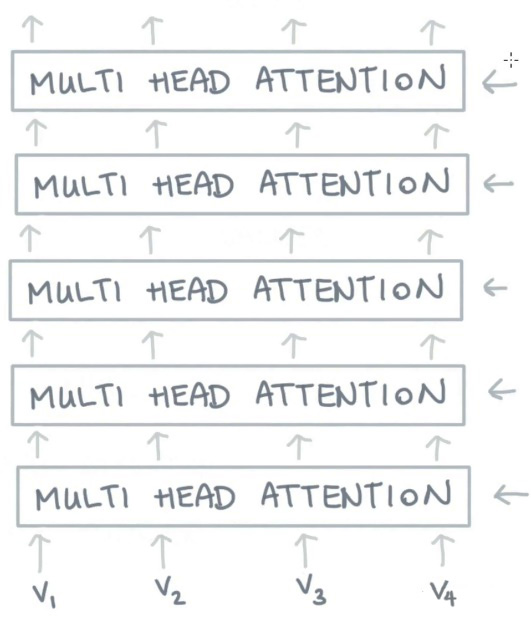
Narrow and wide self-attention

通常，我们有两种方式来实现 Multi-head 的 Self-attention。

  1. 默认的做法是我们会把 Embedding 的向量 $v$ 切割成块，比如说我们有一个 256 大小的 Embedding Vector，并且我们使用8个 Attention Head，那么我们会把这vector 切割成 8 个维度大小为 32 的块。对于每一块，我们生成它的 queries，keys 和 values，它们每一个的 size 都是32，那么也就意味着我们矩阵 $W_q^r,W_k^r,W_v^r$ 的大小都是 32×32 。
  2. 还有一种方法是，我们可以让矩阵 $W_q^r,W_k^r,W_v^r$ 的大小都是 256×256 ，并且把每一个 Attention Head 都应用到全部的 256 维大小的向量上。第一种方法的速度会更快，并且能够更节省内存，第二种方法能够得到更好的结果(同时也花费更多的时间和内存)。这两种方法分别叫做 narrow and wide self-attention。

怎么用 Pytorch/Tensorflow2.0 实现在 Transfomer 中的self-attention

实现 Transformer 中的 Self-attention 过程需要 8 个步骤：

  1. 准备输入
  2. 初始化参数
  3. 获取 key，query 和 value
  4. 给 input1 计算 Attention Score
  5. 计算 Softmax
  6. 给 value 乘上 score
  7. 给 value 加权求和获取 output1
  8. 重复步骤4-7，获取 output2，output3

1. 准备输入

为了简单起见，我们使用3个输入，每个输入都是一个 4 维的向量。

1
2
3
Input 1: [1, 0, 1, 0] 
Input 2: [0, 2, 0, 2]
Input 3: [1, 1, 1, 1]

2. 初始化参数

每一个输入都有三个表示，分别为 key（橙黄色）query（红色）value（紫色）。比如说，每一个表示我们希望是一个 3 维的向量。由于输入是4维，所以我们的参数矩阵为 4×3 维。

后面我们会看到，value 的维度，同样也是我们输出的维度。

为了能够获取这些表示，每一个输入（绿色）要和 key，query 和 value 相乘，在我们例子中，我们使用如下的方式初始化这些参数。

key 的参数：

1
2
3
4
[[0, 0, 1],
 [1, 1, 0],
 [0, 1, 0],
 [1, 1, 0]]

query 的参数：

1
2
3
4
[[1, 0, 1],
 [1, 0, 0],
 [0, 0, 1],
 [0, 1, 1]]

value 的参数：

1
2
3
4
[[0, 2, 0],
 [0, 3, 0],
 [1, 0, 3],
 [1, 1, 0]]

通常在神经网络的初始化过程中，这些参数都是比较小的，一般会在 Gaussian, Xavier and Kaiming distributions 随机采样完成。

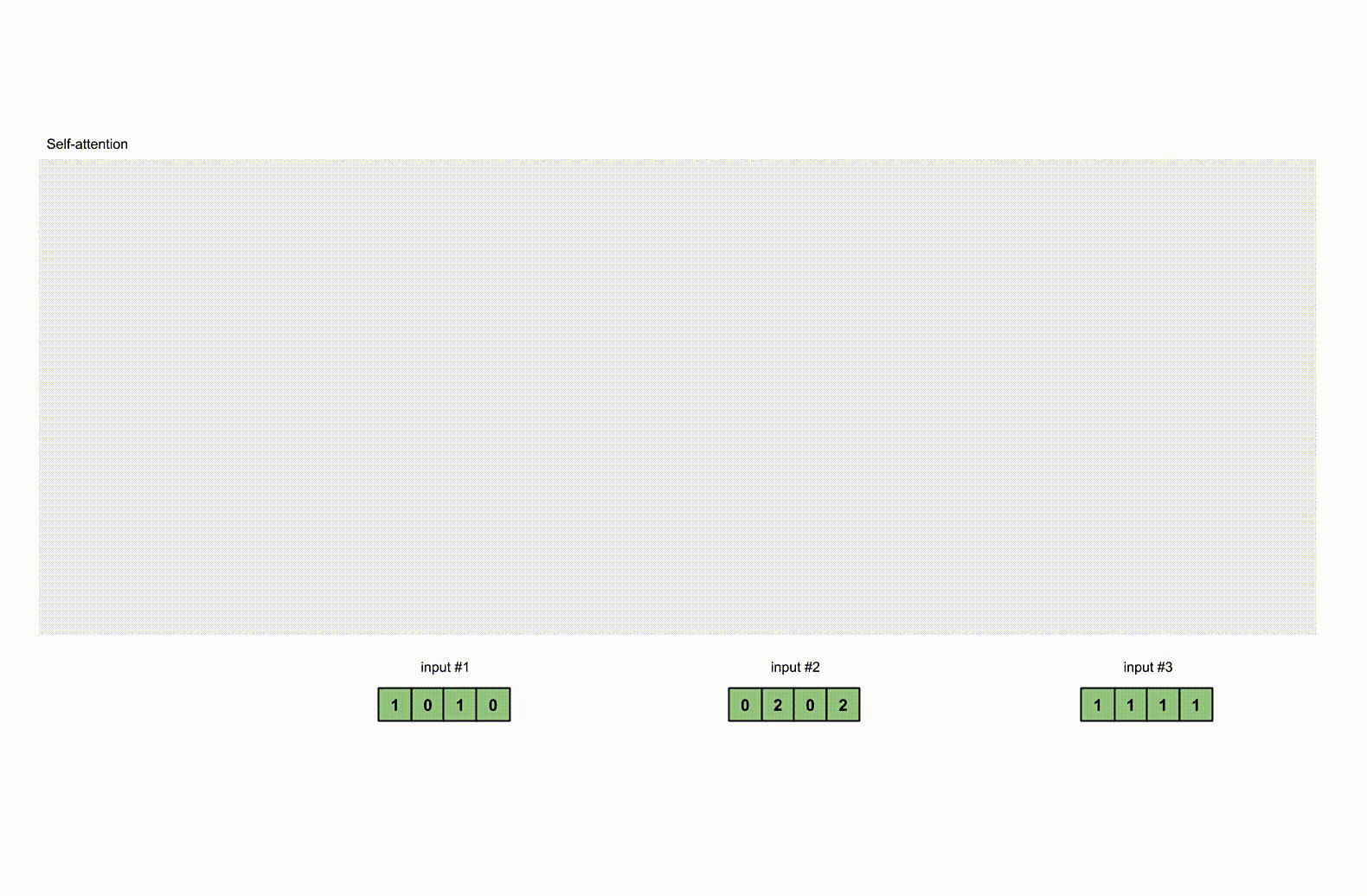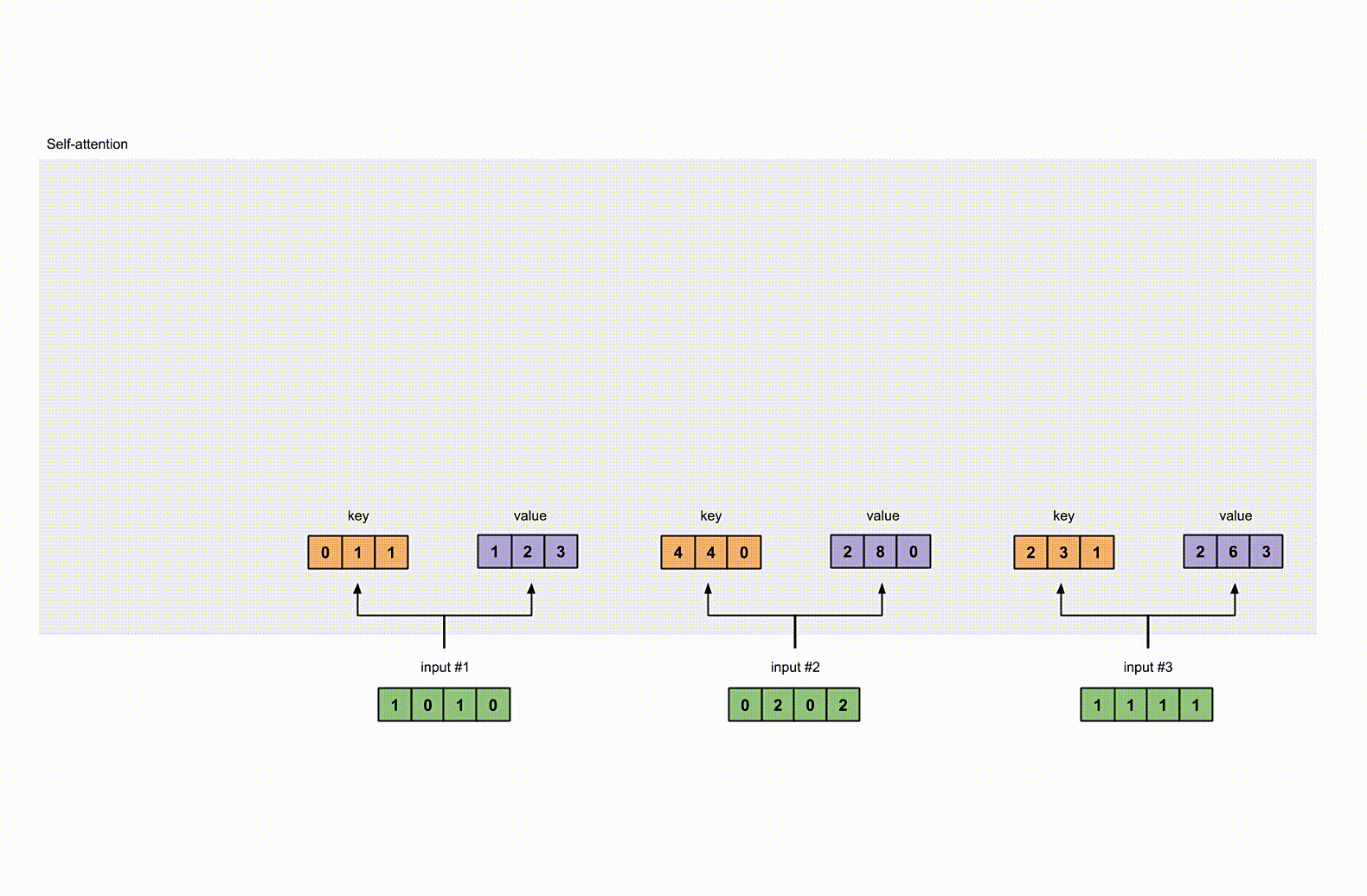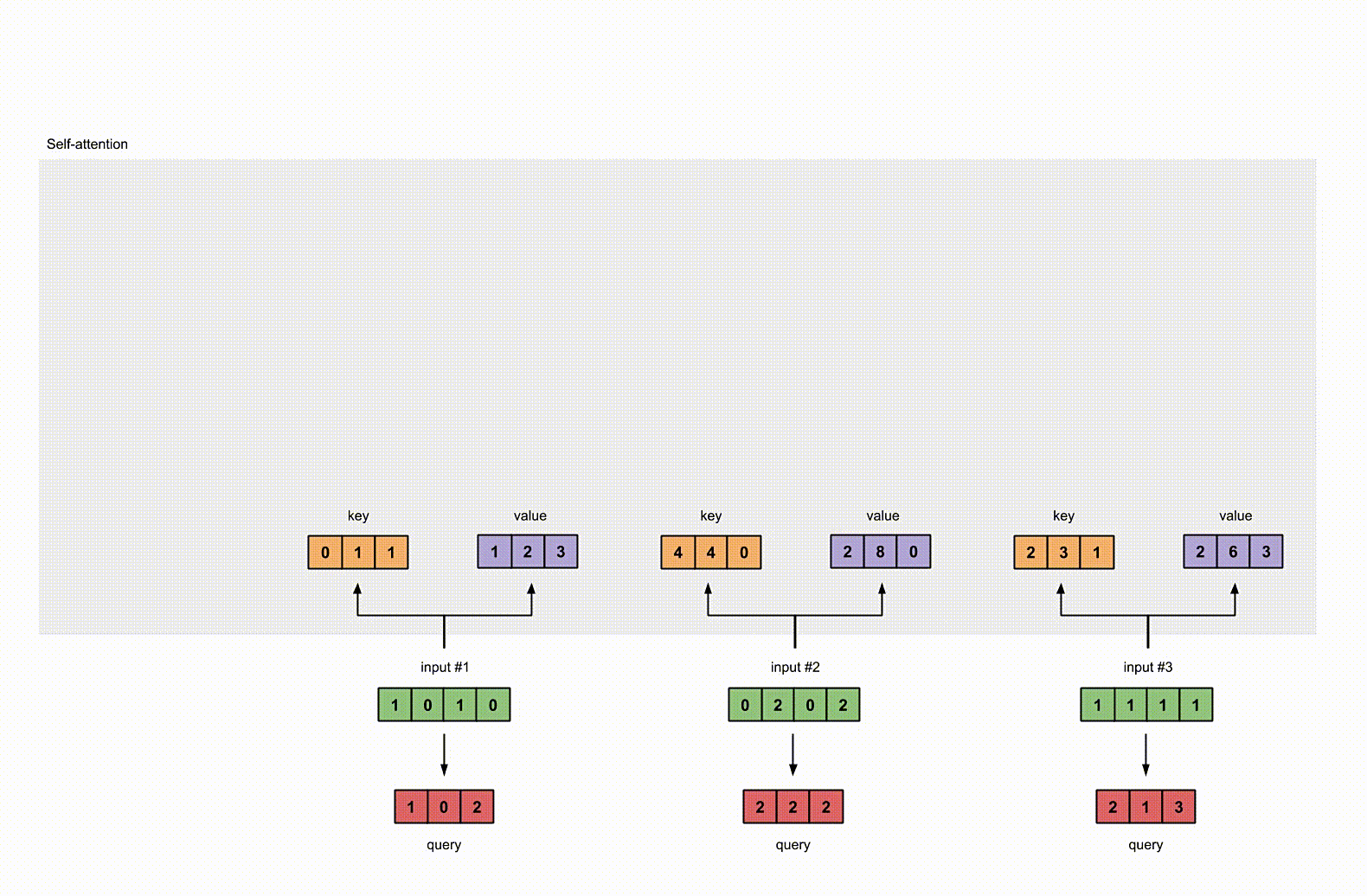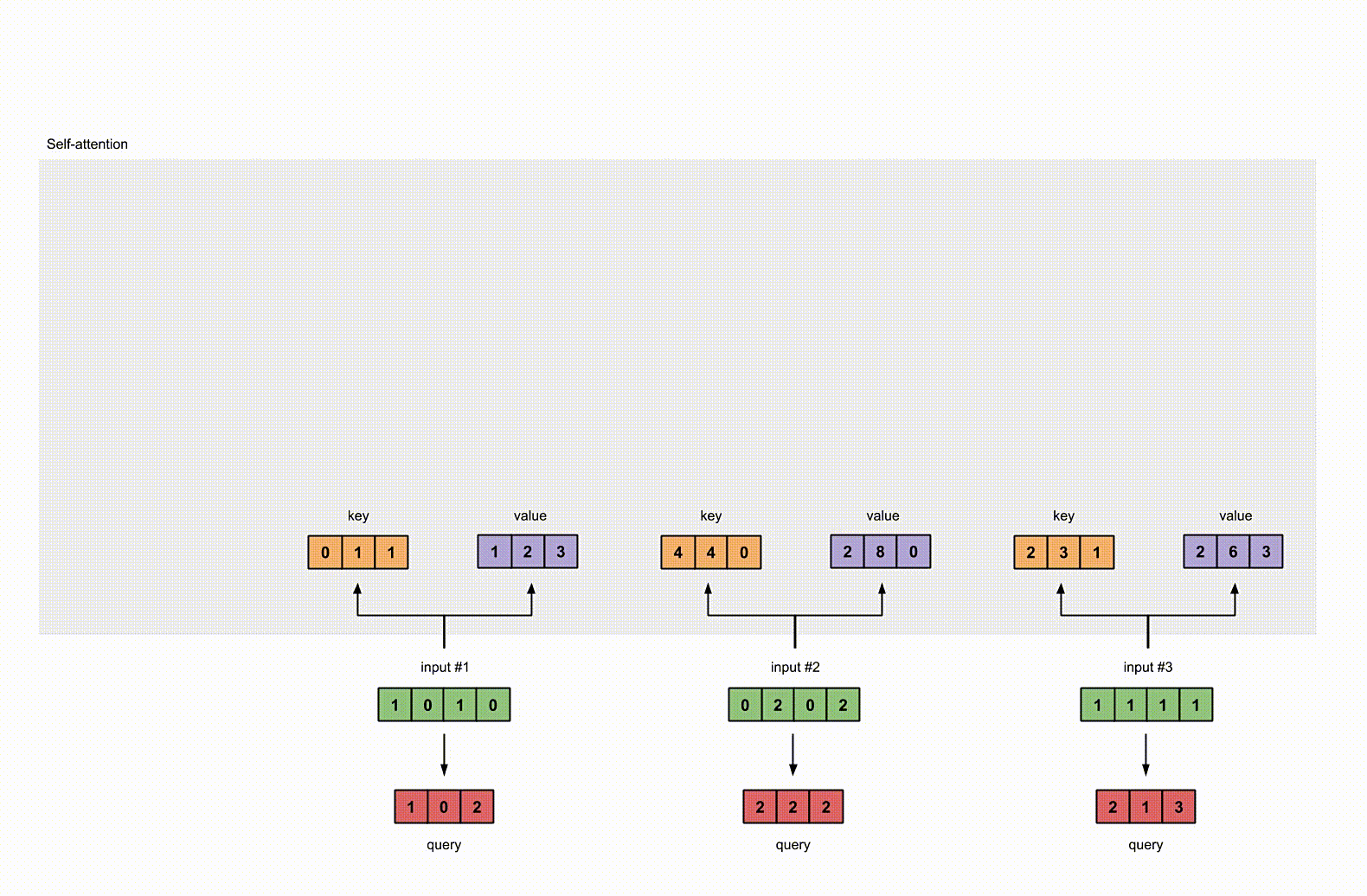
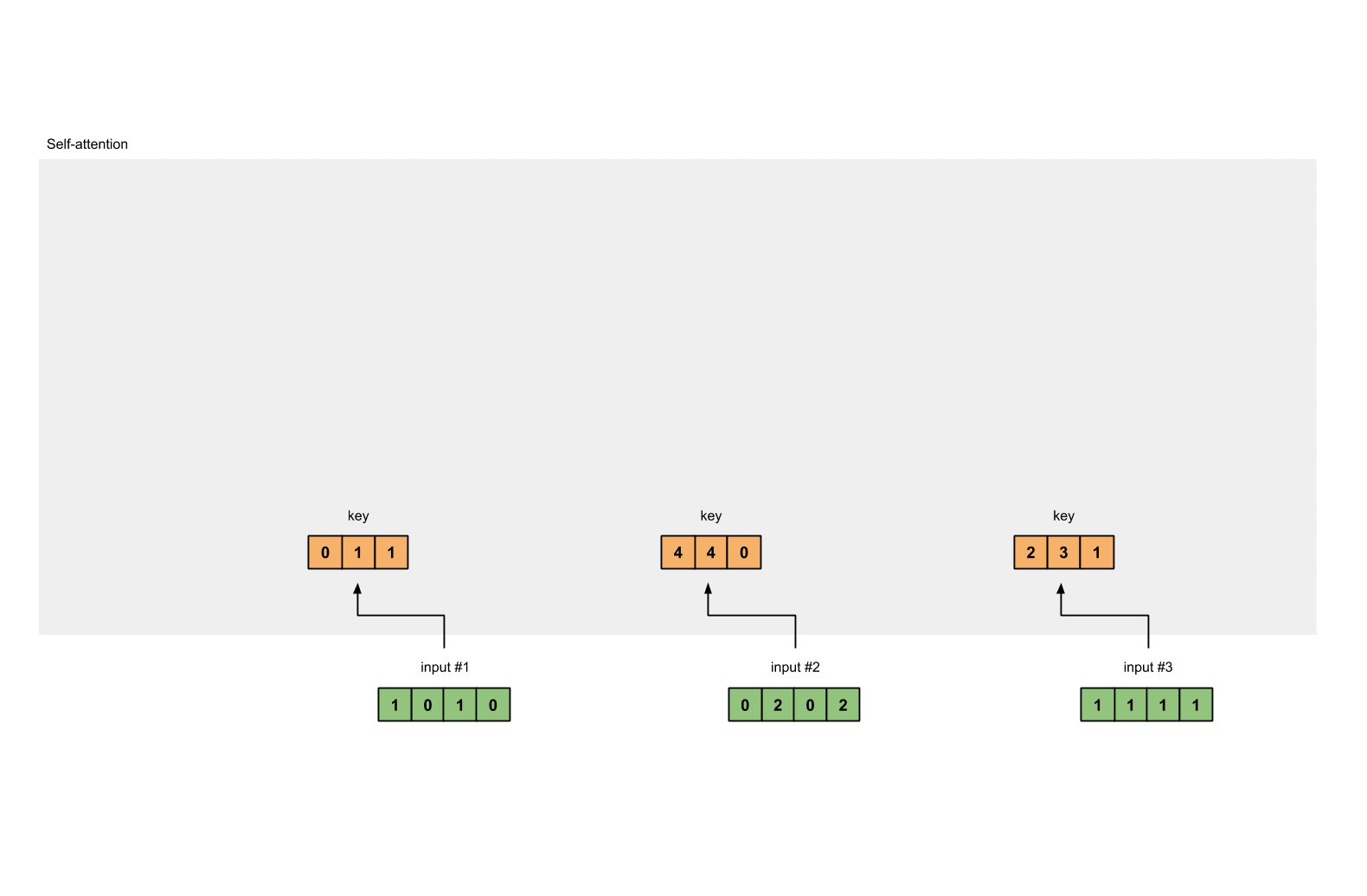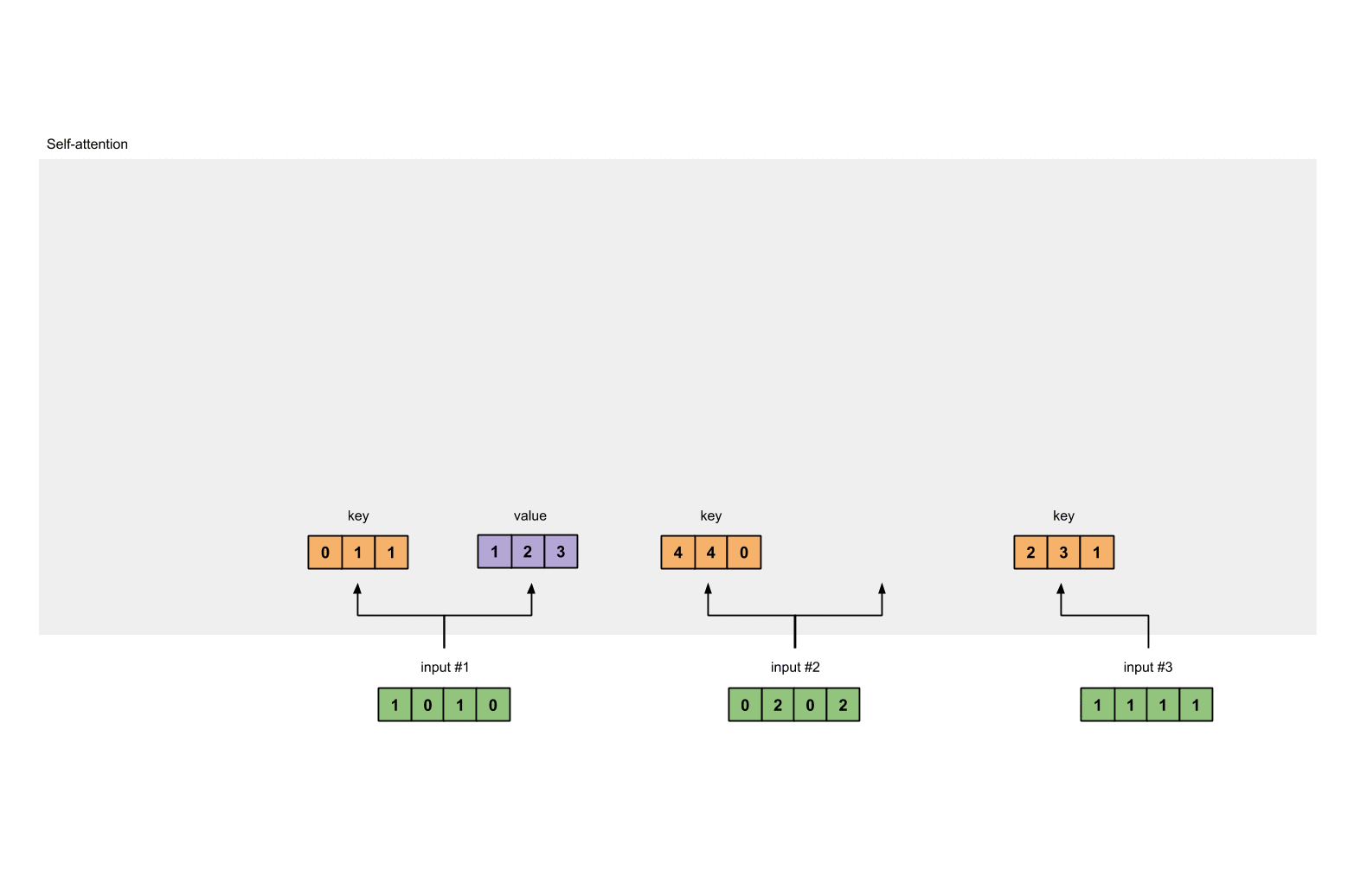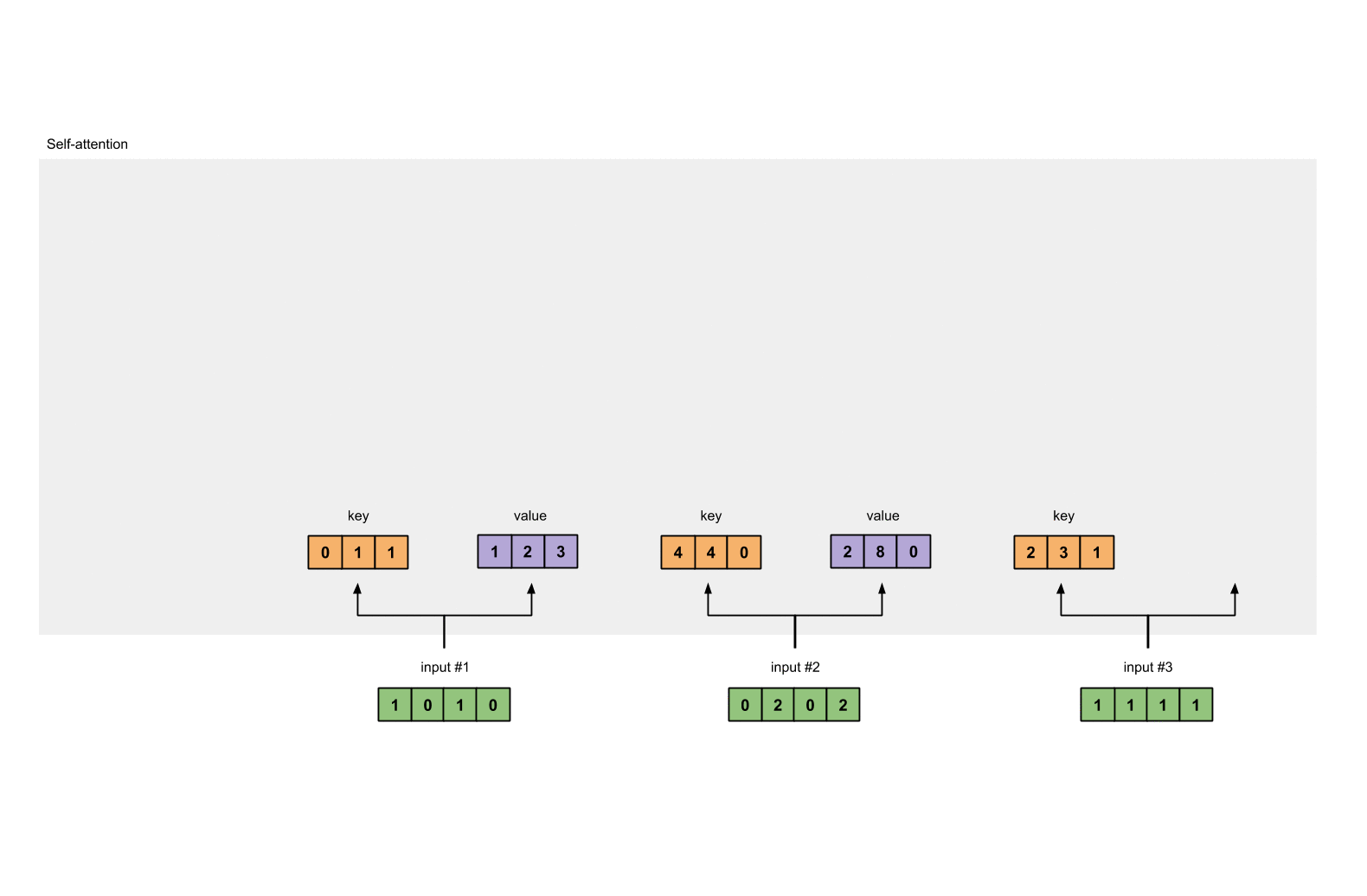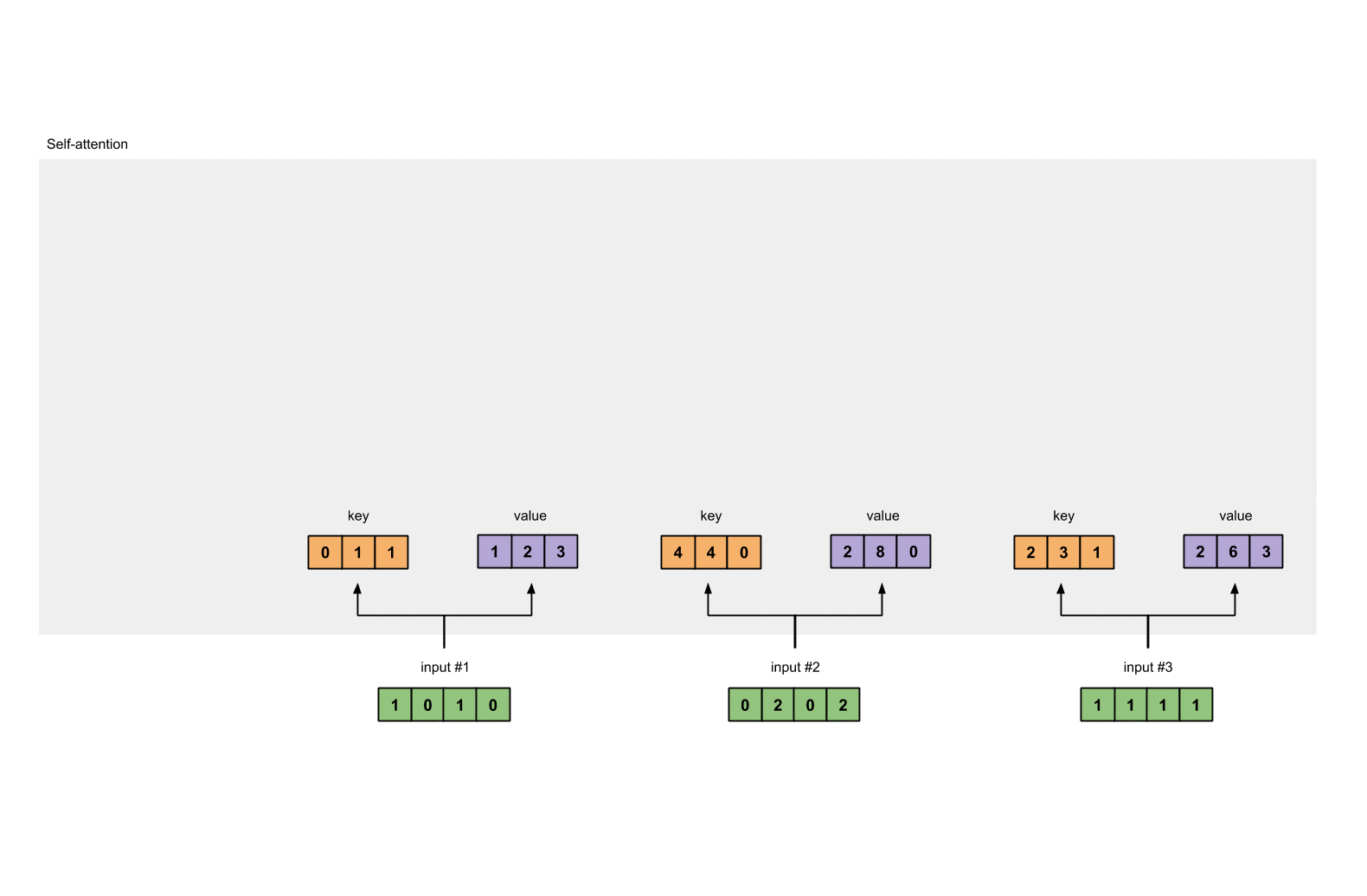
3. 获取 key，query 和 value

现在我们有了三个参数，现在就让我们来获取实际上的key，query和value。

对于 input1 的 key 的表示为：

1
2
3
4
               [0, 0, 1]
[1, 0, 1, 0] x [1, 1, 0] = [0, 1, 1]
               [0, 1, 0]
               [1, 1, 0]

使用相同的参数获取 input2 的 key 的表示：

1
2
3
4
               [0, 0, 1]
[0, 2, 0, 2] x [1, 1, 0] = [4, 4, 0]
               [0, 1, 0]
               [1, 1, 0]

使用参数获取 input3 的 key 的表示：

1
2
3
4
               [0, 0, 1]
[1, 1, 1, 1] x [1, 1, 0] = [2, 3, 1]
               [0, 1, 0]
               [1, 1, 0]

那使用向量化的表示为：

1
2
3
4
               [0, 0, 1]
[1, 0, 1, 0]   [1, 1, 0]   [0, 1, 1]
[0, 2, 0, 2] x [0, 1, 0] = [4, 4, 0]
[1, 1, 1, 1]   [1, 1, 0]   [2, 3, 1]

对 value 做相同的事情。

1
2
3
4
               [0, 2, 0]
[1, 0, 1, 0]   [0, 3, 0]   [1, 2, 3] 
[0, 2, 0, 2] x [1, 0, 3] = [2, 8, 0]
[1, 1, 1, 1]   [1, 1, 0]   [2, 6, 3]

query 也是一样的。

1
2
3
4
               [1, 0, 1]
[1, 0, 1, 0]   [1, 0, 0]   [1, 0, 2]
[0, 2, 0, 2] x [0, 0, 1] = [2, 2, 2]
[1, 1, 1, 1]   [0, 1, 1]   [2, 1, 3]

在我们实际的应用中，有可能会在点乘后，加上一个 bias 的向量。

4. 给 input1 计算 attention score

为了获取 input1 的 attention score，我们使用点乘来处理所有的 key 和 query，包括它自己的 key 和 value。这样我们就能够得到 3 个 key 的表示（因为我们有3个输入），我们就获得了3个 attention score（蓝色）。

1
2
3
           [0, 4, 2]
[1, 0, 2] x [1, 4, 3] = [2, 4, 4]
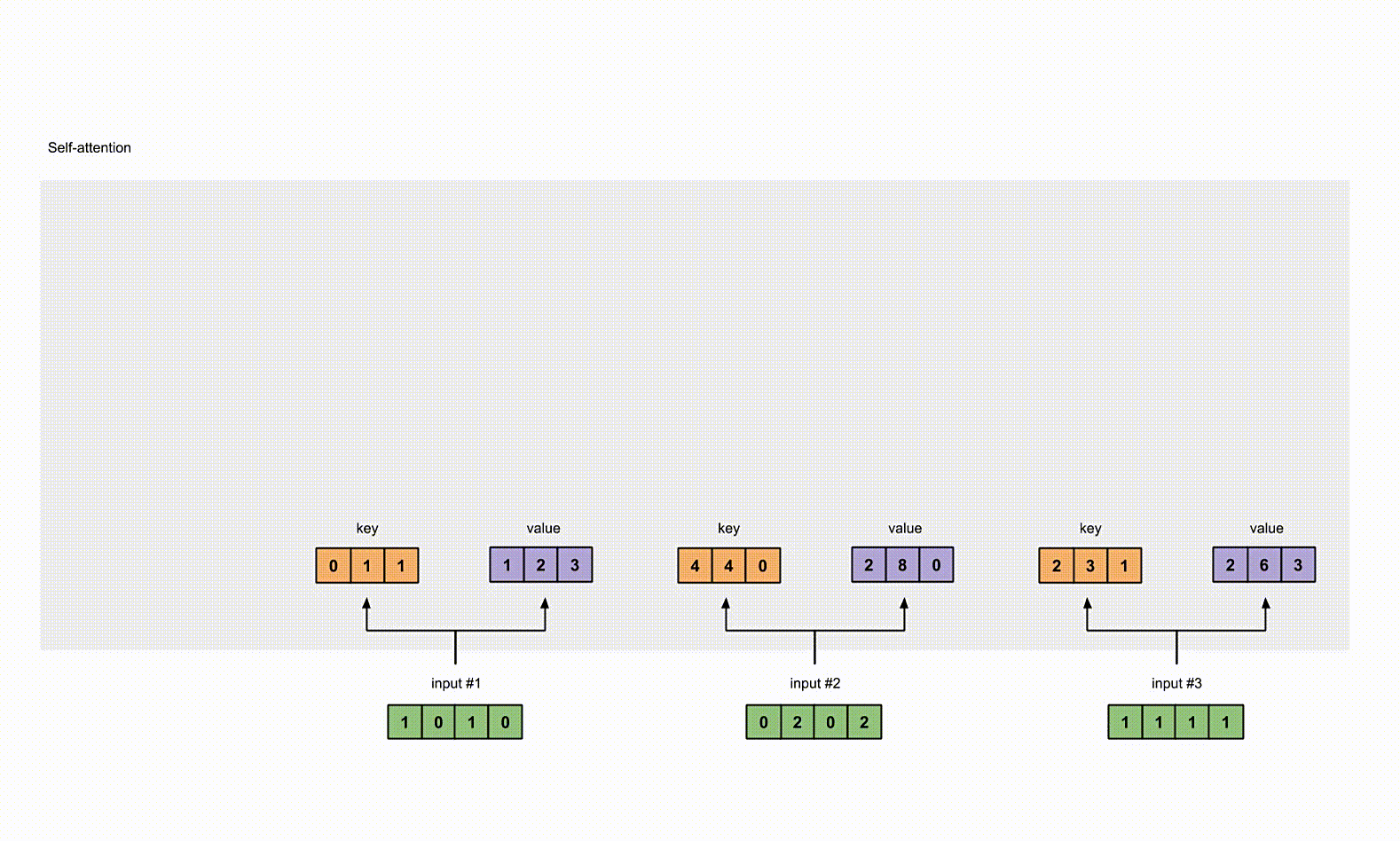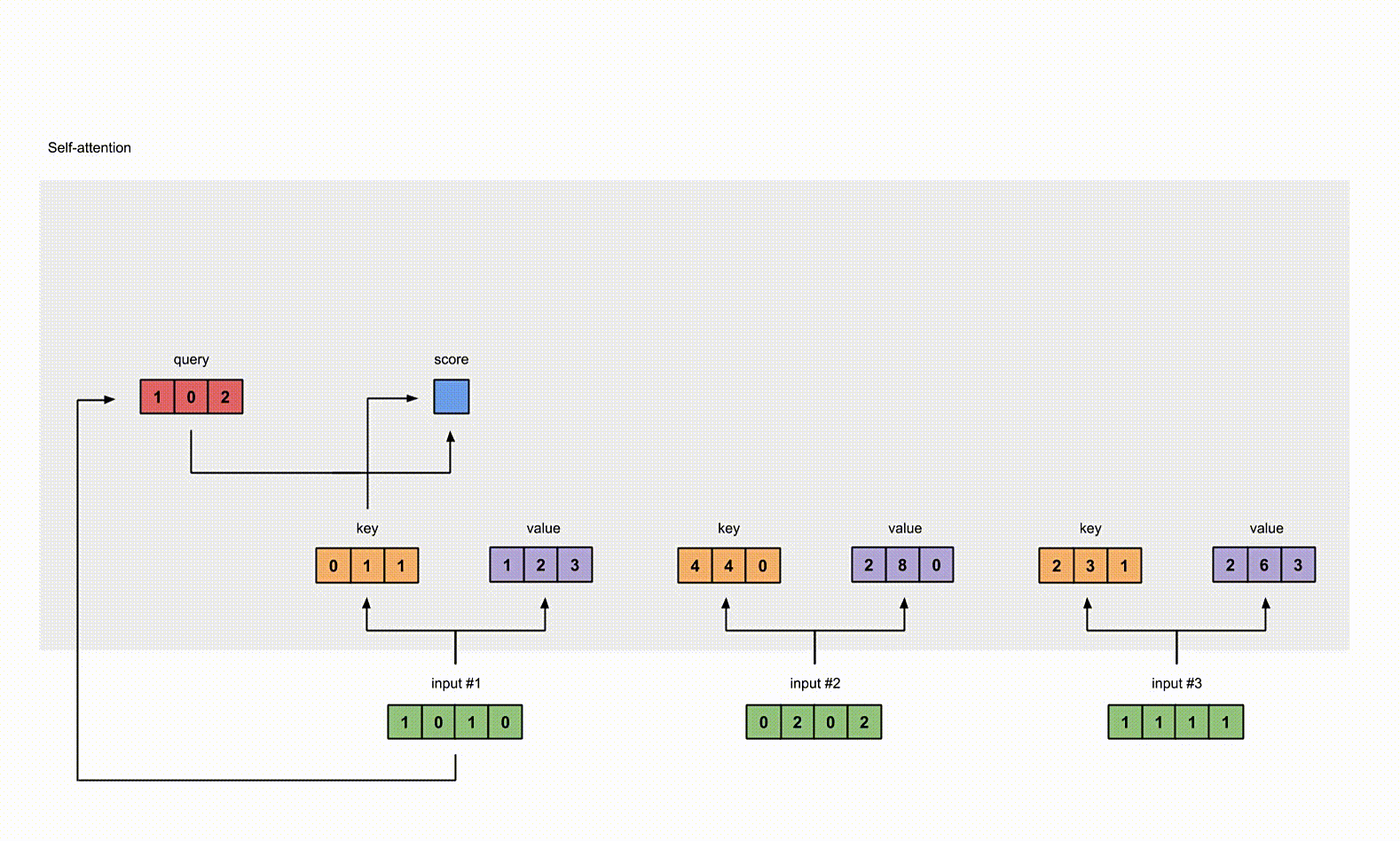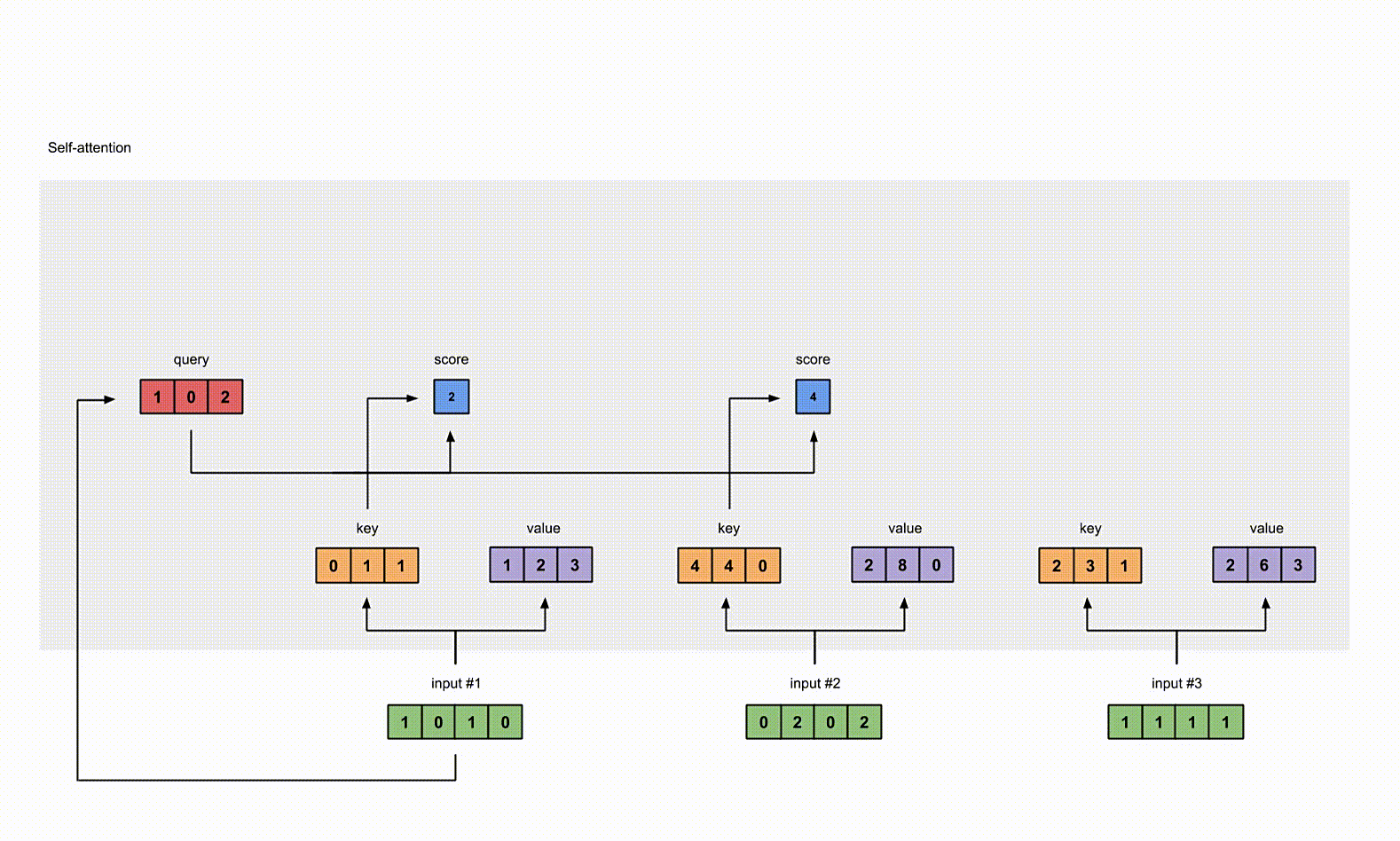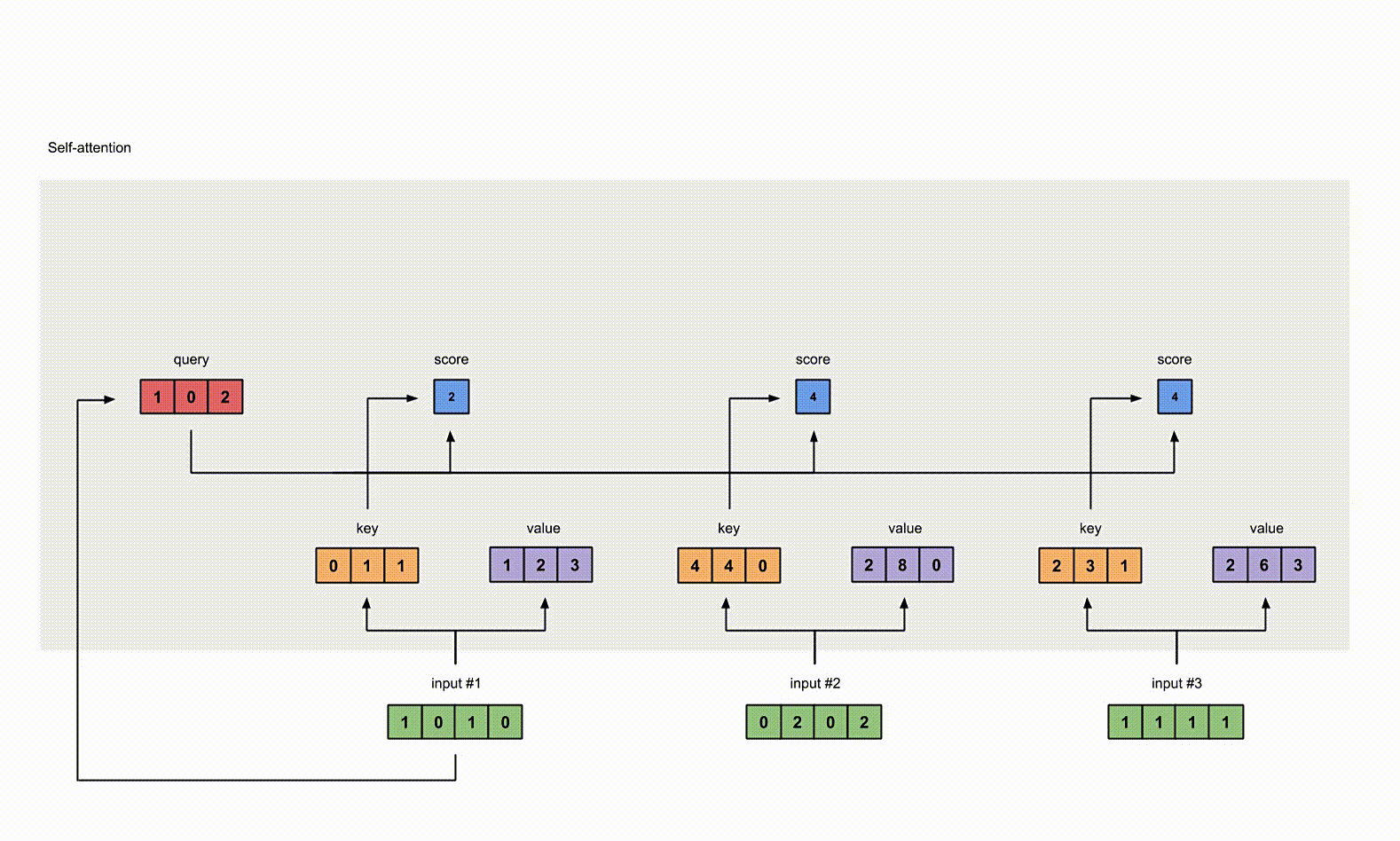
            [1, 0, 1]

这里我们需要注意一下，这里我们只有 input1 的例子。后面，我们会对其他的输入的 query 做相同的操作。

5. 计算 Softmax

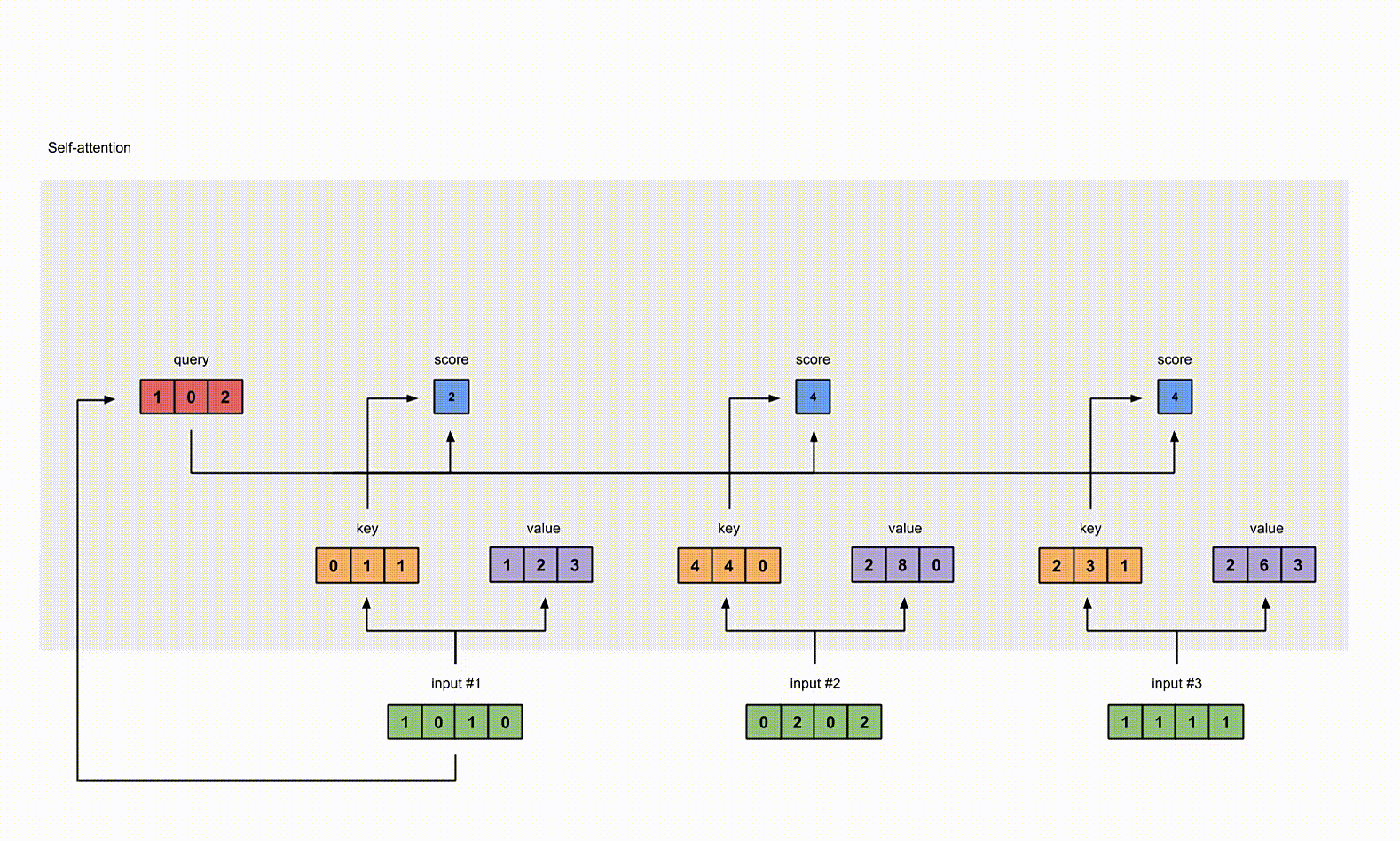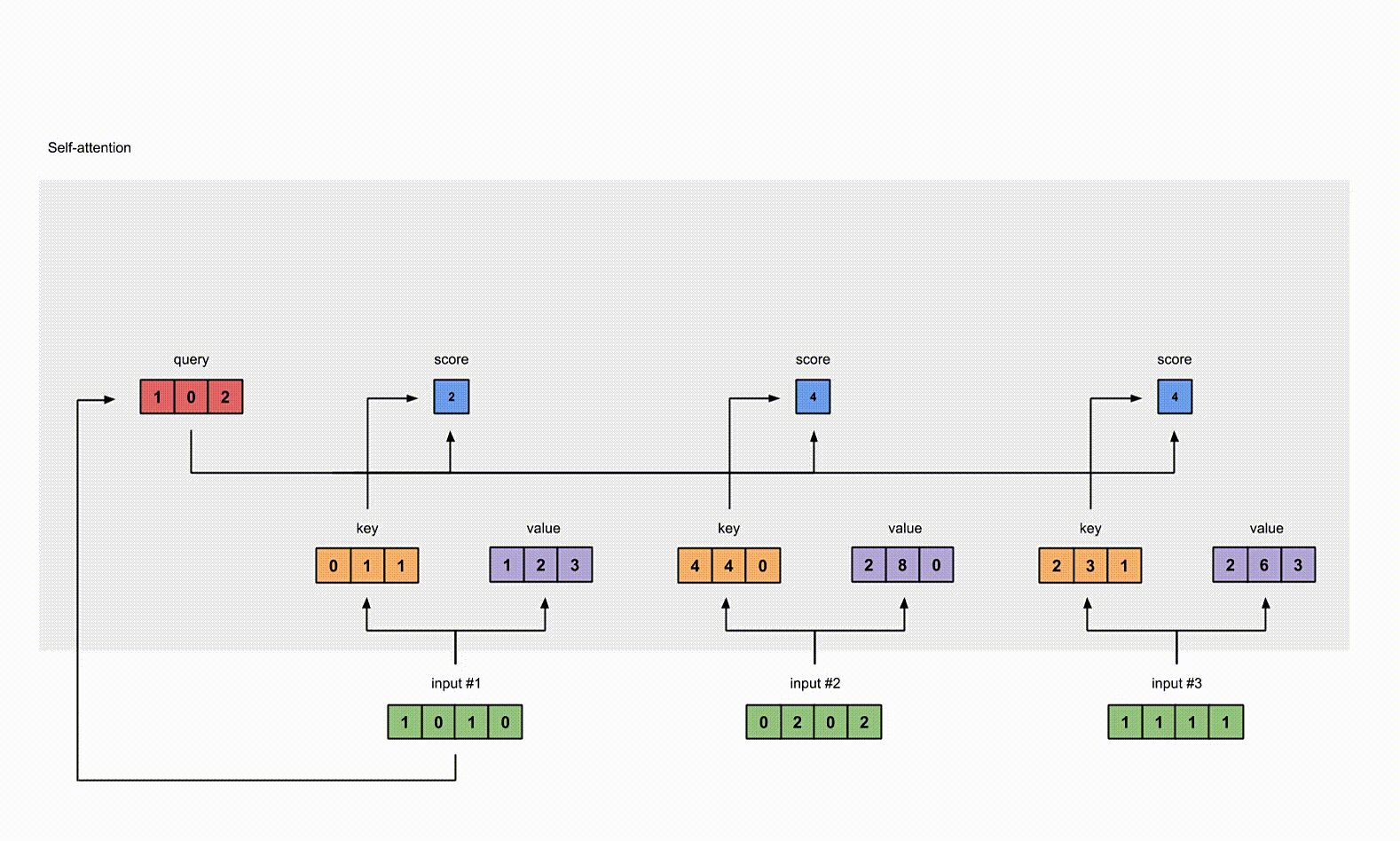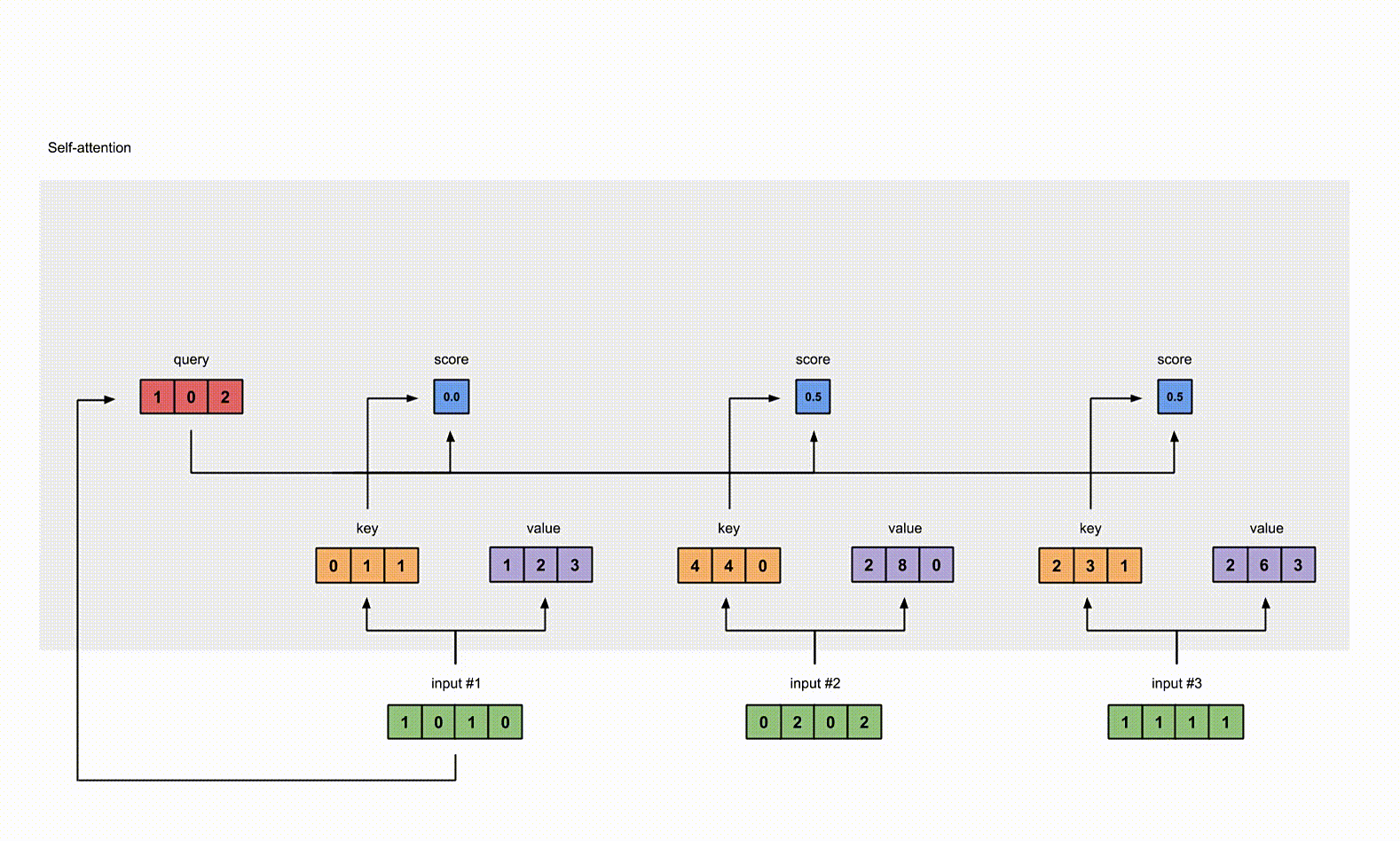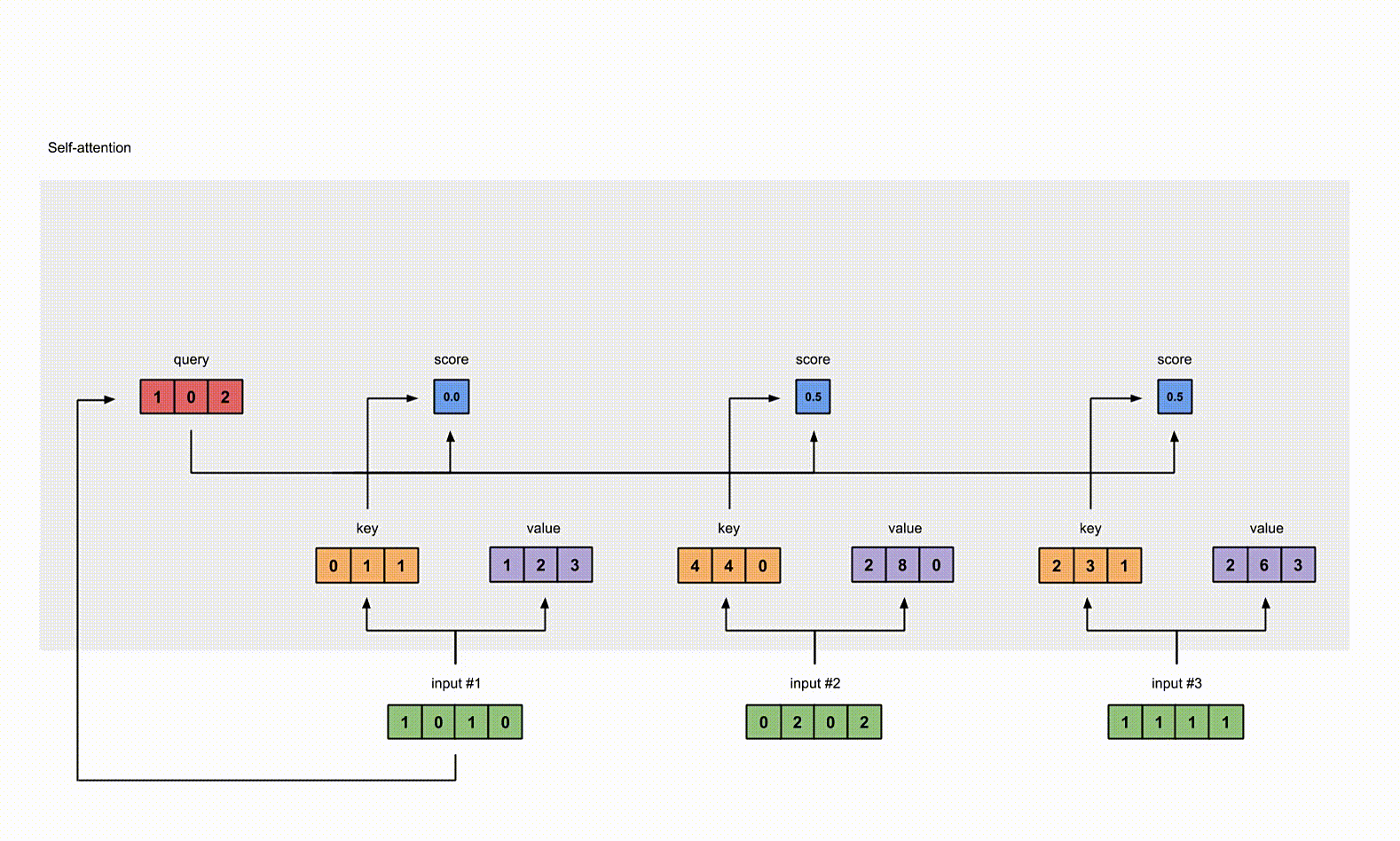
给 attention score 应用 Softmax。

为了计算简便，softmax 结果近似一下

1
softmax([2, 4, 4]) = [0.063, 0.468, 0.468] ≈ [0, 0.5, 0.5]

6. 给 value 乘上 score

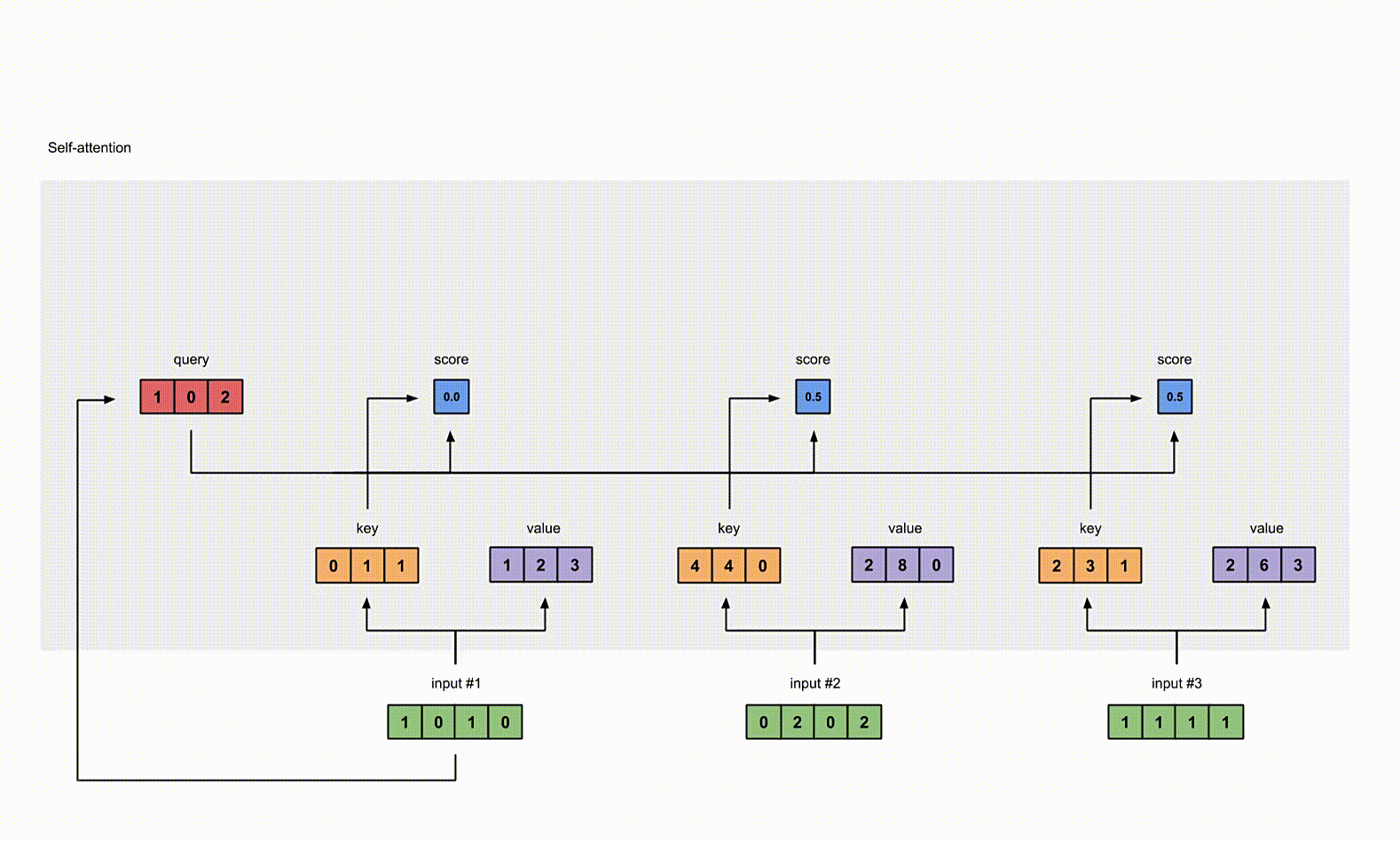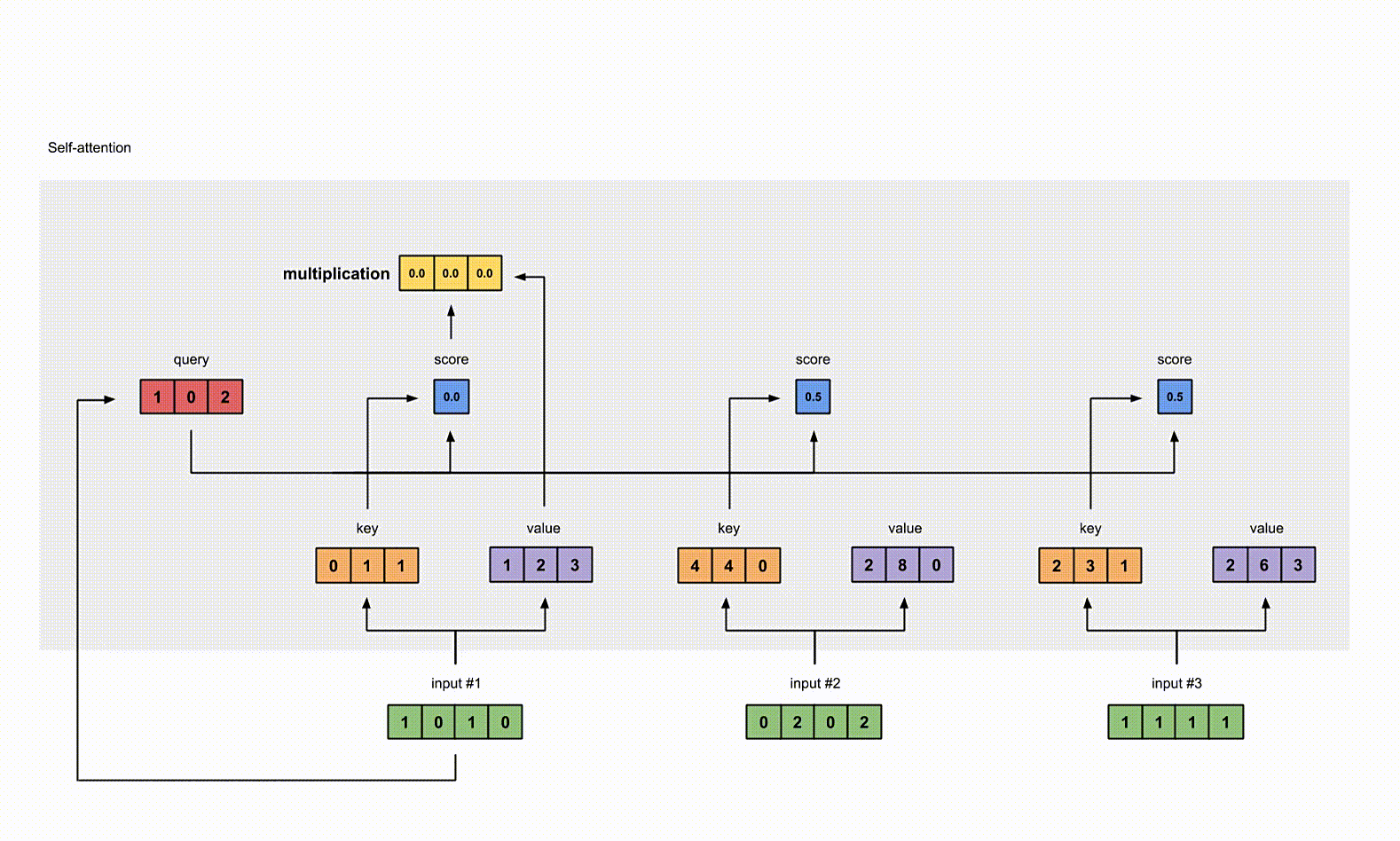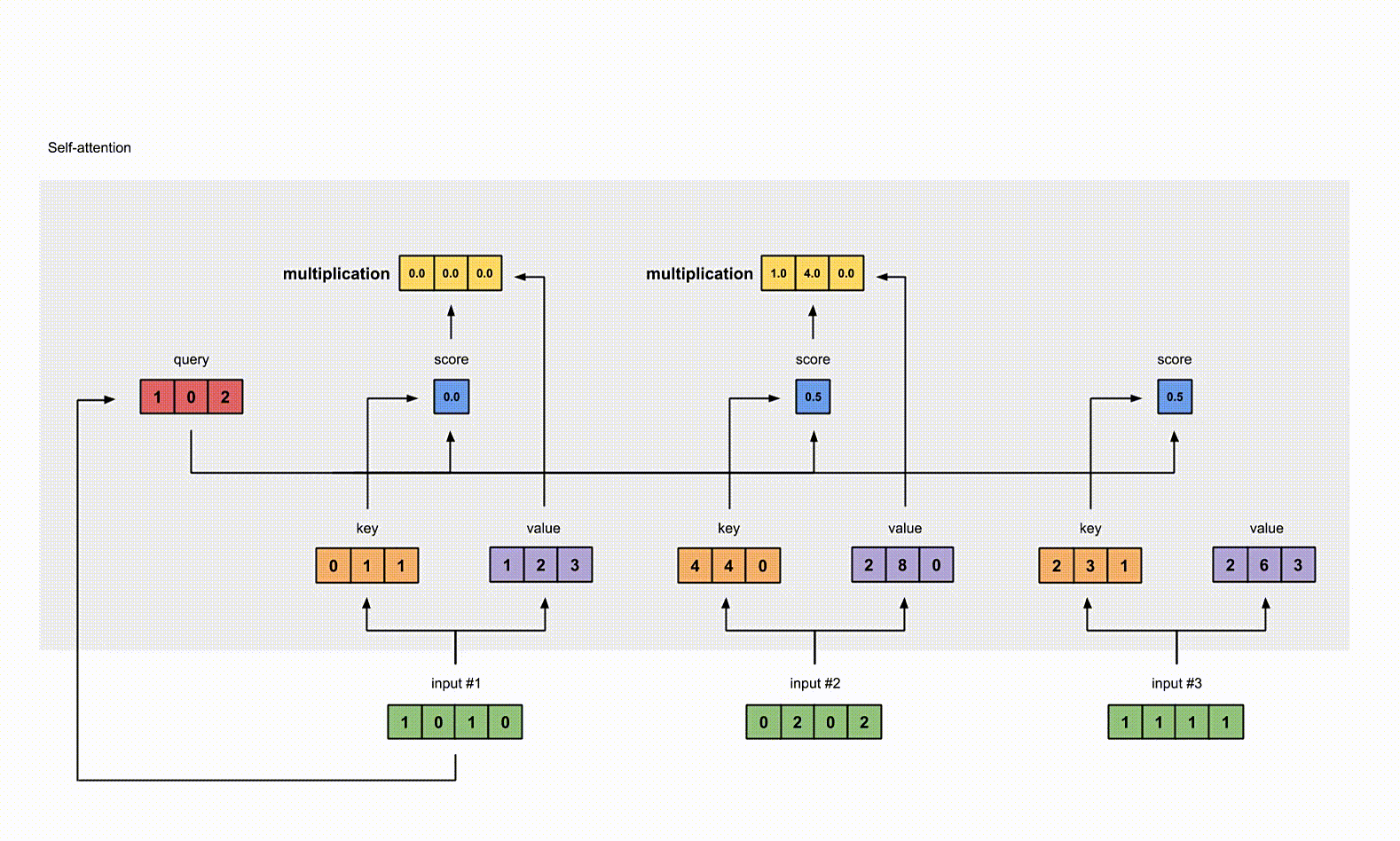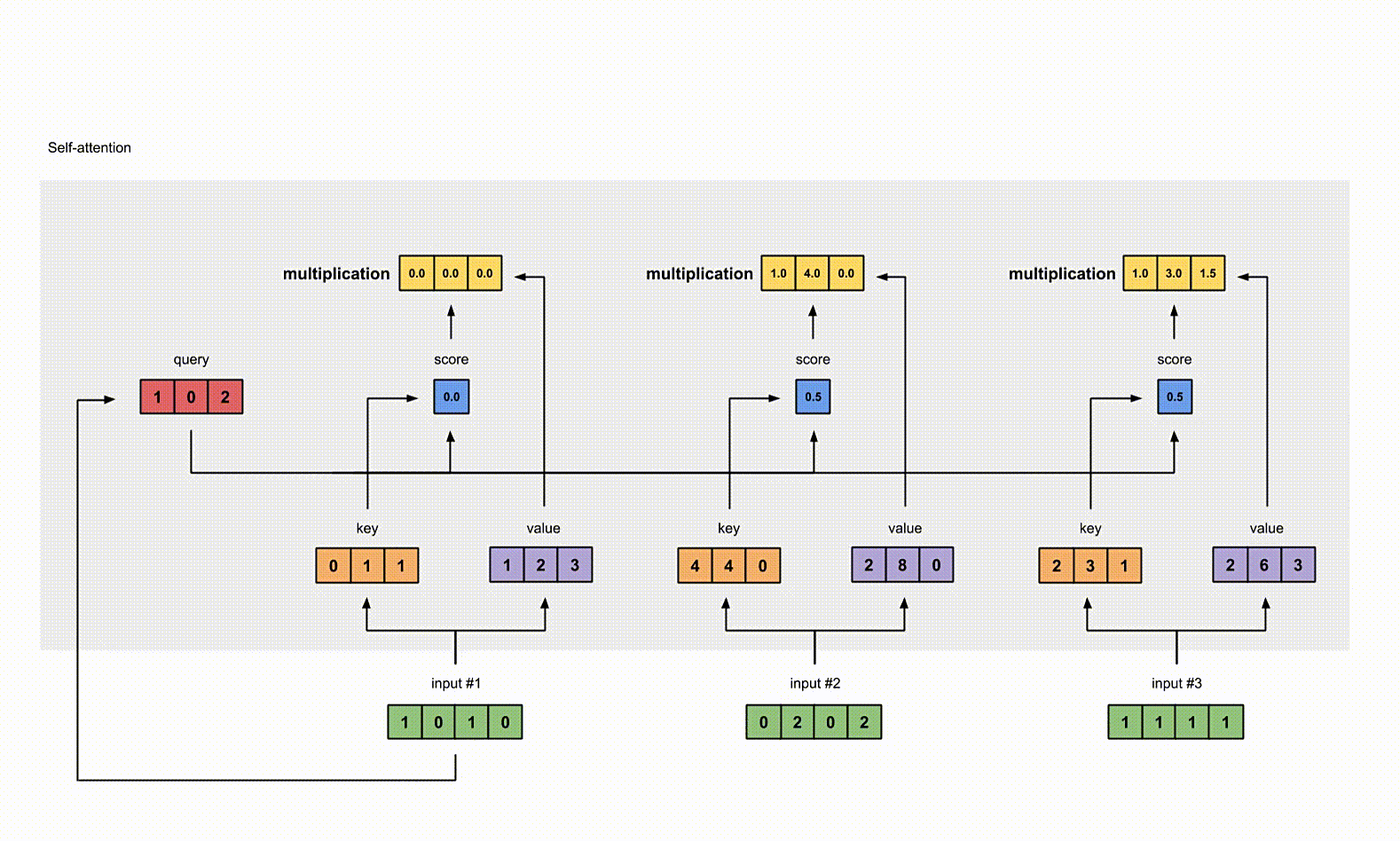
使用经过 softmax 后的 attention score 乘以它对应的 value 值（紫色），这样我们就得到了3个 weighted values（黄色）。

1
2
3
1: 0 * [1, 2, 3] = [0.0, 0.0, 0.0]
2: 0.5 * [2, 8, 0] = [1.0, 4.0, 0.0]
3: 0.5 * [2, 6, 3] = [1.0, 3.0, 1.5]

7. 给 value 加权求和获取 output1

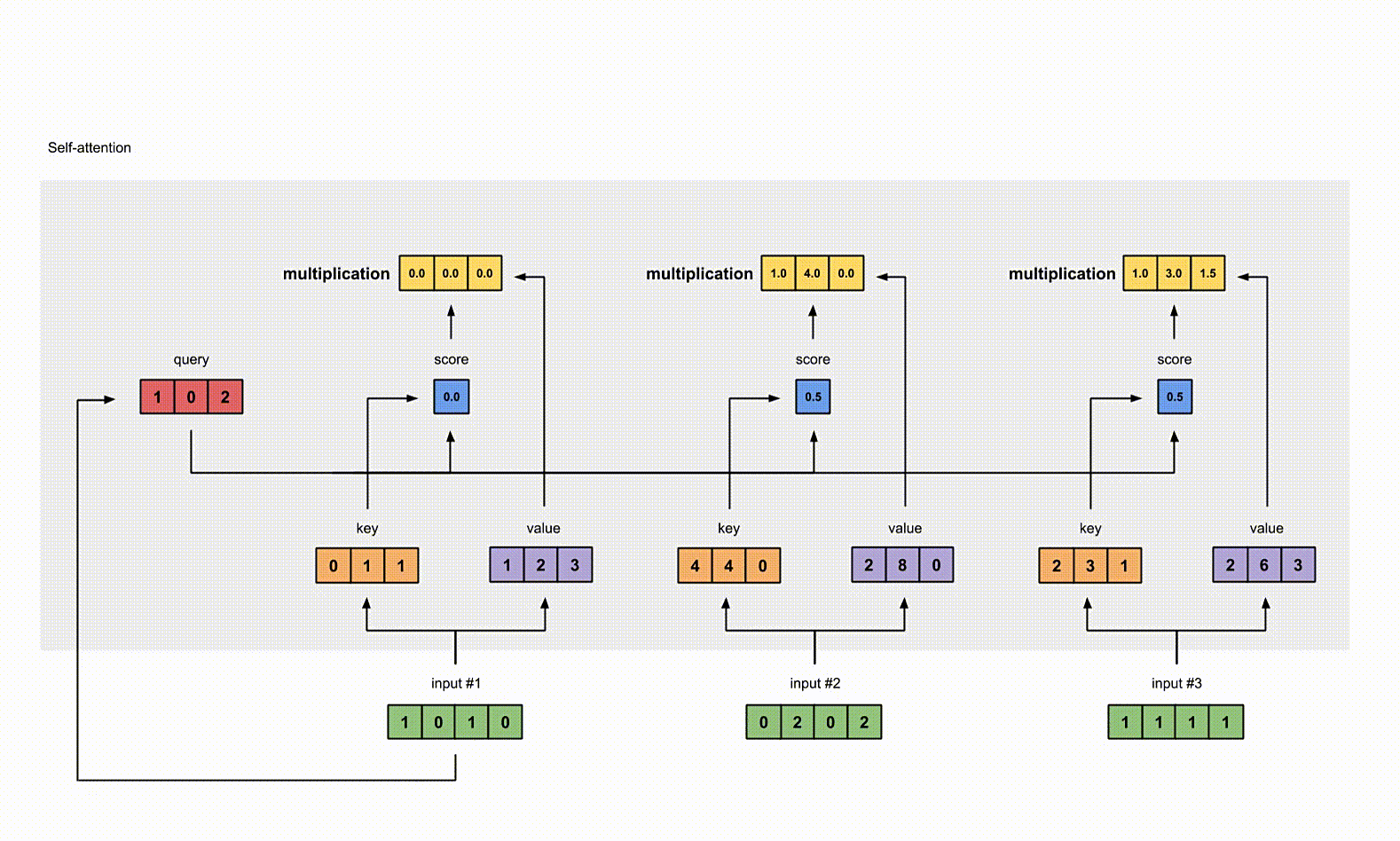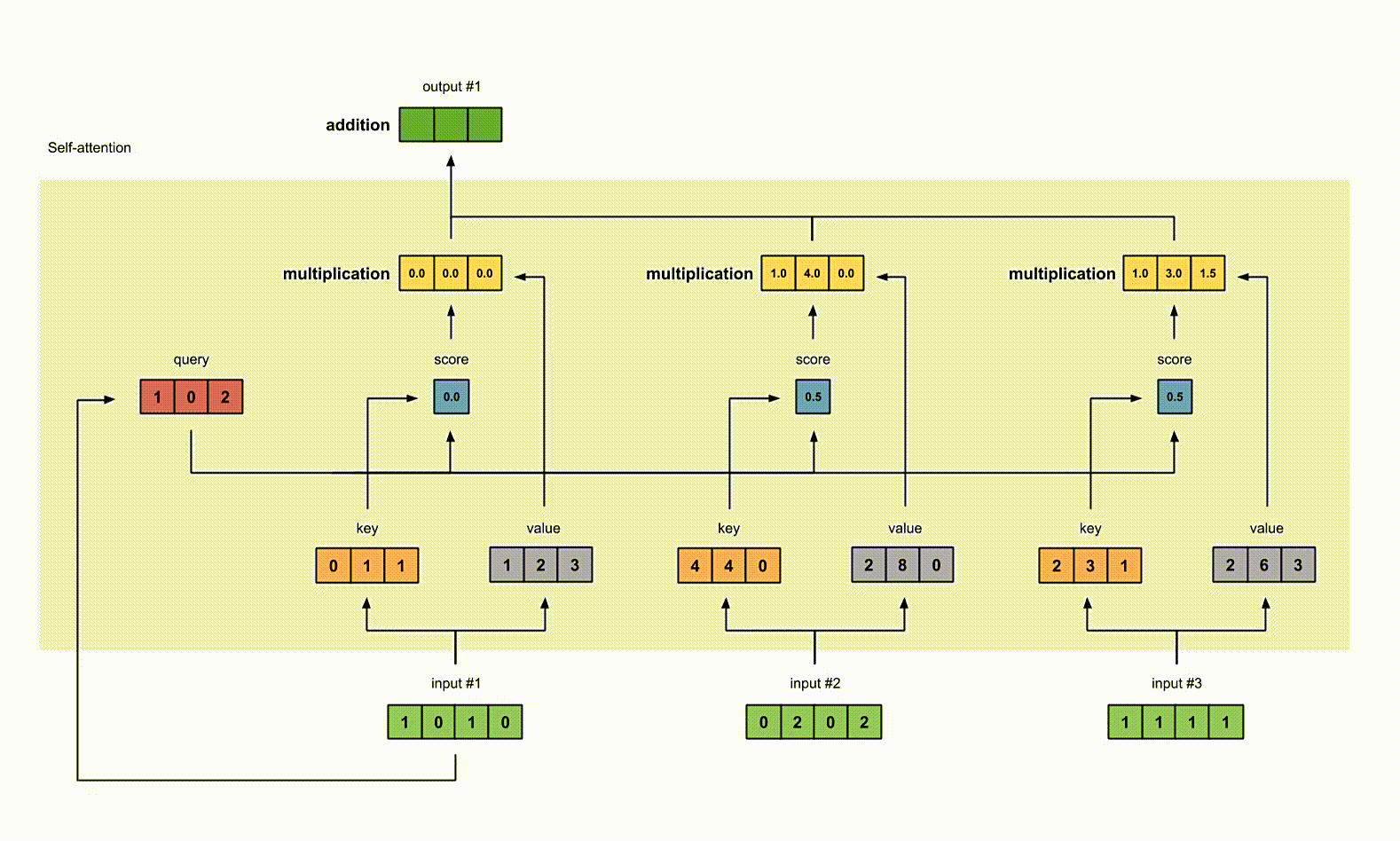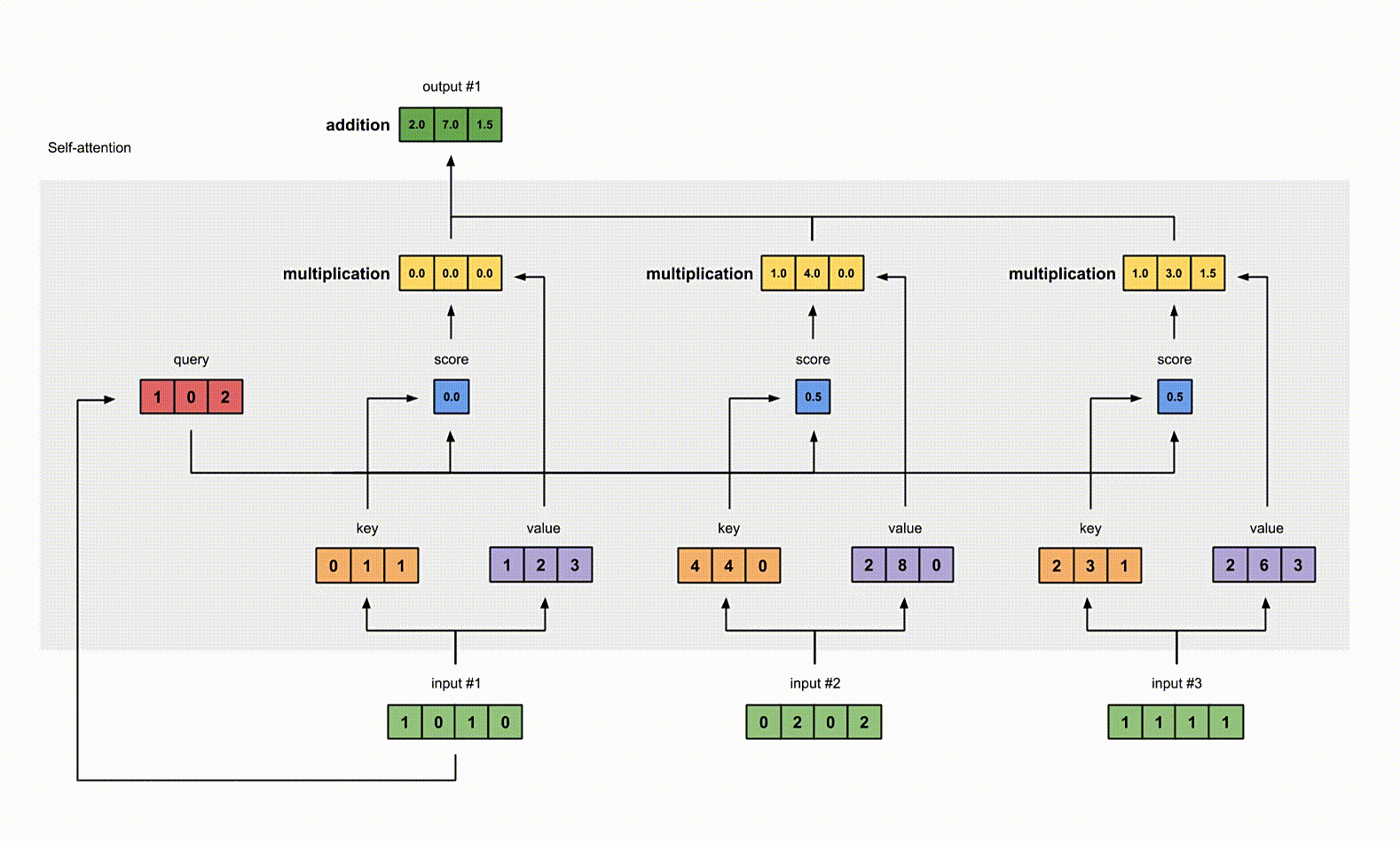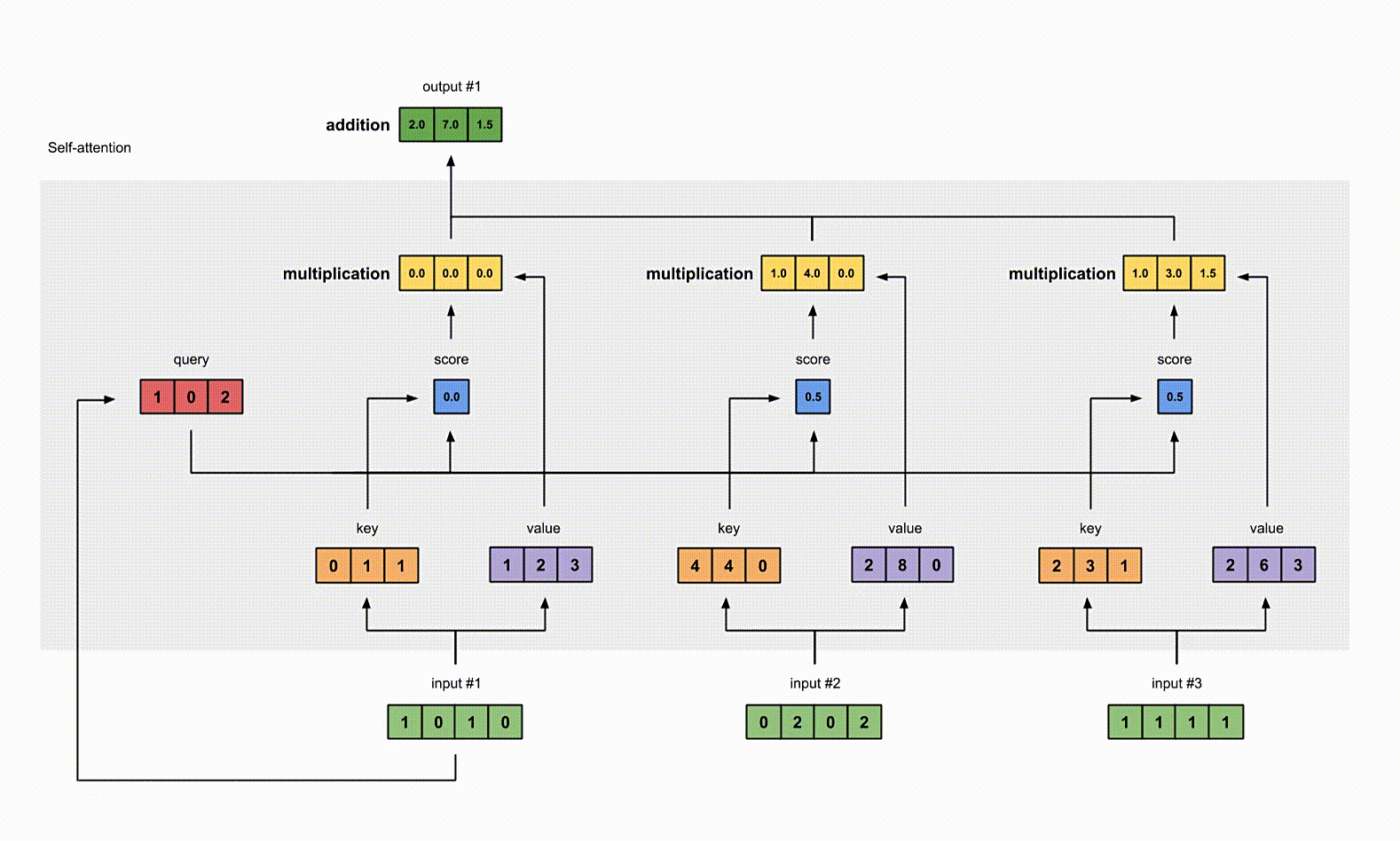
把所有的 weighted values（黄色）进行 element-wise 的相加。

1
2
3
4
5
  [0.0, 0.0, 0.0]
+ [1.0, 4.0, 0.0]
+ [1.0, 3.0, 1.5]
-----------------
= [2.0, 7.0, 1.5]

得到结果向量 [2.0, 7.0, 1.5]（深绿色）就是 ouput1 的和其他 key 交互的 query representation。

8. 重复步骤4-7，获取 output2，output3

现在，我们已经完成 output1 的全部计算，我们要对 input2 和 input3 也重复的完成步骤4～7的计算。

大神的代码仓库：

https://github.com/CYang828/transformer-all-in-one

参考资料



文章链接：
https://www.zywvvd.com/notes/study/deep-learning/transformer/transformer-intr/transformer-intr-2/

“觉得不错的话，给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信二维码

微信支付

支付宝二维码

支付宝支付

Deep_Learning > Transformer
#Deep_Learning #Transformer
Transformer - 2 - Transformer 中的 Self-attenstion
https://www.zywvvd.com/notes/study/deep-learning/transformer/transformer-intr/transformer-intr-2/
作者
Yiwei Zhang
发布于
2023年5月6日
许可协议