本文最后更新于:2024年5月7日 下午
随着神经网络的发展,注意力模型已经被广泛的应用到自然语言处理,统计学习语音识别和计算机视觉等人工智能相关领域。
简介
Attention机制:又称为注意力机制,顾名思义,是一种能让模型对重要信息重点关注并充分学习吸收的技术.通俗的讲就是把注意力集中放在重要的点上,而忽略其他不重要的因素。其中重要程度的判断取决于应用场景,根据应用场景的不同,Attention分为空间注意力和时间注意力,前者用于图像处理,后者用于自然语言处理.
注意力机制的灵感来源可以归结到人对环境的生理感知上来。比方说,我们的视觉系统更倾向于去挑选影像中的部分信息进行集中分析而忽略掉图像中的无关信息。与此类似,很多设计到语言,语音和视觉的问题中都包含与研究任务密切相关的信息,同时也包含着一些无关的信息。比方说,在文本翻译和总结任务中,可能只有输入序列的某些单词与我们的下一个预测输出值有关;在图像标注任务中,可能某些局部信息与下一个标注单词联系更为密切。注意力机制将这种相关系进行了整合,允许模型动态地去关注输入的特定部分从而更为有效地完成手头的任务。
在神经网络结构中加入注意力模型主要是基于三点考虑:
- 首先是这些模型在众多的任务中取得了非常好的性能,比方说机器翻译、问答系统、情感分析、词性标注选民分析和问答系统。
- 在提升模型性能的同时,注意力机制增加了神经网络结构的可解释性。由于传统的神经网络是一个黑盒模型,因此提高其可解释性对机器学习模型的公平性、可靠性和透明性的提高至关重要。
- 能够帮助缓解递归神经网络中的一些缺陷,比方说随着输入序列长度的增加导致的性能下降和对输入的顺序处理所导致的计算效率低下。本文的目的在于对注意力模型进行一个简单且易理解的介绍。
序列模型
一个经典的序列模型 (sequence-to-sequence) 包含一个编码部分和一个解码部分。编码器通常采用一个循环神经网络结构来对序列的输入${x _ { 1 }, x _ { 2 }, \cdots , x _ { T } }$ 进行编码得到一组固定长度的编码向量 $ {h_ { 1}, h_ { 2}, \cdots, h_ { T } } $。解码器同样利用一个RNN结构读取单个输入 $ h_{T} $组固定长度的编码向量 $ {h_ { 1 }, h _ { 2 }, \cdots , h _ { T } } $ 。解码器同样利用一个RNN结构读取单个输入 $ h_{T} $ 然后一个接一个的进行输出得到一个输出序列 $ {x_ {1 }, x_{2 }, \cdots, x_{T ^ { \prime}} } $ 。其中 $ T $ 和 $ T^{\prime} $ 分别代表输入和输出序列的长度。在每个位置$ t, h_{t} $ 和 $ s_{t} $分别代表该位置编码器和解码器的隐藏状态。
传统编码的弊端
注意力机制最早用在 seq2seq 模型上**,**原始编解码模型的encode过程会生成一个中间向量C,用于保存原序列的语义信息。但是这个向量长度是固定的,当输入原序列的长度比较长时,向量C无法保存全部的语义信息,上下文语义信息受到了限制,这也限制了模型的理解能力。

常规的编码方法,无法体现对一个句子序列中不同语素的关注程度,在自然语言中,一个句子中的不同部分是有不同含义和重要性的,比如:I hate this movie。 如果是做情感分析的应用场景,训练的时候明显应该对hate这个词语做更多的关注。
注意力模型 Attention
注意力模型通过允许解码器访问所有编码器产生的输出 $ {h_{1}, h_{2}, \cdots, h_ { T}} $ 来克服传统结构的缺点。其核心思想是对编码器的所有输出进行加权组合后输入到当前位置的解码器中来影响解码器的输出。通过对编码器的输出进行加权,在实现输入与输出的对齐的同时还能够利用更多的原始数据的上下文信息。
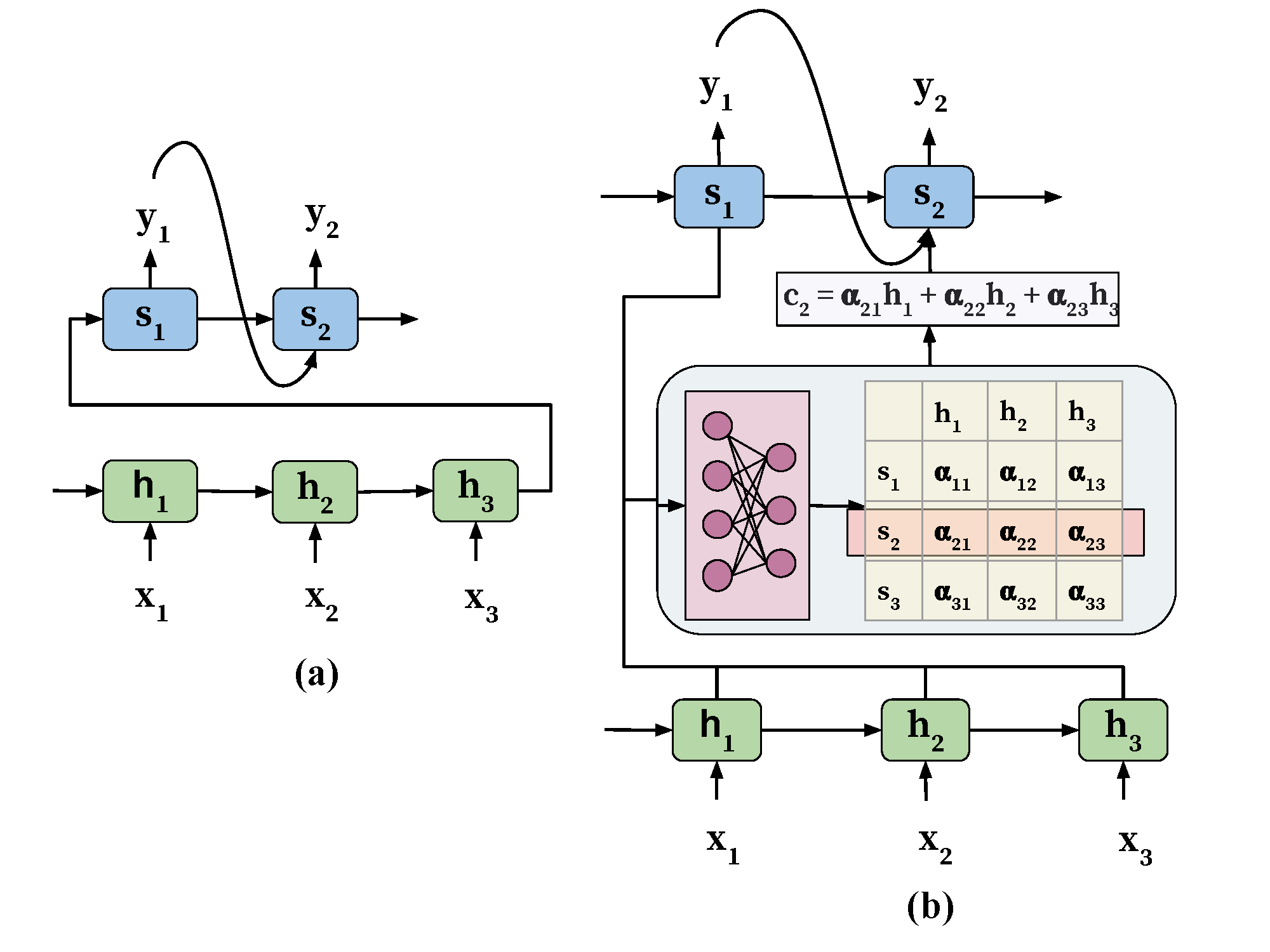
注意力机制的引入
引入注意力机制的模型的结构如图(b)所示。注意力模块能够自动地学习权重 $ \alpha_{i j} $ 用来捕捉编码器隐藏状态$ h_{i} $和解码器隐藏状态$ s_{j} $ 的相关性。习得的这些注意力权重将会被用来构建一个上下文向量 $ c $ 来作为解码器的输入。在解码器的每个位置 $ j $,上下文向量 $ c_{j} $ 是由注意力权重对所有的编码器的隐藏状态进行加权求和进行得到的,即: $ c_{j}=\sum_{i=1}^{T^{\prime}} \alpha_{i j} h_{i} $ 。于是, 这一上下文向量其实为解码器提供了一种访问整个输入序列并且关注序列中的特定相关位置的一种机制,我们称这 种机制为注意力机制。
基本流程
以 seq2seq 模型为例子,对于一个句子序列$S$,其由单词序列$[w_1,w_2,w_3,…,w_n]$构成:
- 将$S$的每个单词 $ w_{i} $ 编码为一个单独向量 $ v_{i} $, 这里对应seq2seq模型, 就是在encoder编码阶段,每个时间步单位(即每个单词)的输出隐状态。
- 在解码decoder阶段,待预测词的输入隐状态$C$(即上一个时间步的输出状态)与 (1) 中每个单词的隐状态相乘再做 softmax 归一化后得到权重分数,使用学习到的注意力权重 $ a_{i} $ 对 (1) 中得到的所有单词向量做加权线性组合 $ Z=\sum_{i} a_{i} v_{i} $。
- 利用输入状态$C$以及输入变量$Z$作为对待预测词的共同输入,来进行预测。
具体描述
我们的最终目标是要能够帮助decoder在生成词语时,有一个不同词语的权重的参考。在训练时,对于decoder我们是有训练目标的,此时将decoder中的信息定义为一个Query。而encoder中包含了所有可能出现的词语,我们将其作为一个字典,该字典的key为所有encoder的序列信息。n个单词相当于当前字典中有n条记录,而字典的value通常也是所有encoder的序列信息。
上面对应于第一步,然后是第二部计算注意力权重,由于我们要让模型自己去学习该对哪些语素重点关注,因此要用我们的学习目标Query来参与这个过程,因此对于Query的每个向量,通过一个函数 $ a_{i}=F\left(Q_{i}, K\right) $,计算预测i时刻词时,需要学习的注意力权重,由于包含n个单词,因此, $a_i$ 应当是一个n维的向量,为了后续计算方便,需要将该向量进行softmax归一化,让向量的每一维元素都是一个概率值。
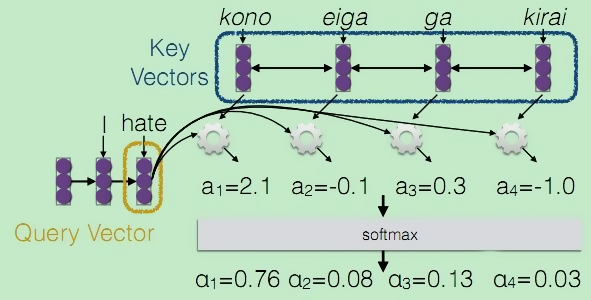
最后对Value vectors进行加权线性组合,得到带权重参考的“字典”输出:
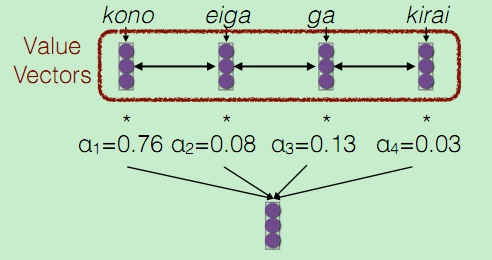
此处Value 和 Key 是相同的。
Q,K,V
Query , Key 和 Value 是注意力机制的几个核心概念,刚接触时总是难以理解,个人总结一些要点辅助理顺思路:
- 注意力最终的目的是从已经编码好的 Value 中挑出一组线性组合和 Query 最相关
- 那么就需要计算每一组 Value 和当前 Query 的相关程度了
- 可以认为 Key 和 Value 是一一绑定的,我们通过计算 Query 和每一组 Key 的相关性来得到 Query 和 Value 的相关性
- 将计算得到的相关性向量做 softmax 得到加权系数
- 用这个加权系数线性组合 Value 得到解码后的特征
注意力权重的学习
注意力权重的学习是通过在原始的网络结构中增加一个前馈网络来实现的。这一前馈网络的注意力权重的值$ \alpha_{i j} $是编码器隐藏状态值 $ h_{j} $和解码器内部隐藏状态值$ \boldsymbol{S}_{i-1} $的函数。该前馈网络可以与之前的网络结构一起进行训练。
那么如何计算 Query 和 key 的注意力权重$\alpha$呢?
这里总结了几种方法:
- 多层感知机方法
$$
a(q, k)=w_{2}^{T} \tanh \left(W_{1}[q ; k]\right)
$$
主要是先将query和key进行拼接,然后接一个激活函数为 $tanh$ 的全连接层,然后再与一个网络定义的权重矩阵做乘积。这种方法据说对于大规模的数据特别有效。
- Bilinear方法
$$
a(q, k)=q^{T} W k
$$
通过一个权重矩阵直接建立q和k的关系映射,比较直接,且计算速度较快。
- Dot Product
$$
a(q, k)=q^{T} k
$$
这个方法更直接,连权重矩阵都省了,直接建立q和k的关系映射,优点是计算速度更快了,且不需要参数,降低了模型的复杂度。但是需要q和k的维度要相同。
- scaled-dot Product
$$
a(q, k)=\frac{q^{T} k}{\sqrt{|k|}}
$$
上面的点积方法有一个问题,就是随着向量维度的增加,最后得到的权重也会增加,为了提升计算效率,防止数据上溢,对其进行scaling。
可解释性
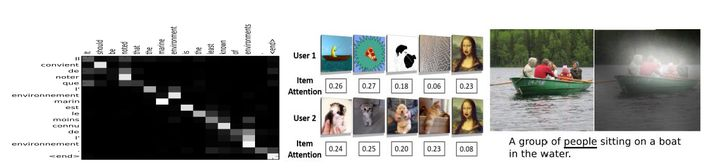
人们对人工智能模型的可解释性有着巨大的兴趣,这是由模型的性能、透明度和公平性驱动的。然而,神经网络,尤其是深度学习结构因其不可预测性而受到批评。从可解释性的角度来看,注意力模型特别有趣,因为它允许我们直接检查深度学习体系结构的内部工作。针对输入和输出均为一个序列的问题,注意力模型的一个重要假设是学习得到的注意力权重体现了当前需输出的数据与输入序列的某些特定位置数据的相关性。为了验证这一假设,我们可以通过对一组输入输出序列对进行可视化。
研究人员将注意力权重可视化,尽管不同语言的主语-动名词位置不同,但法语和英语的句子自动对齐的效果很明显。在一般情况下,注意模型通过正确地将海洋环境与海洋环境进行比对,显示出非单调的一致性。
自注意力模型 Self-Attention
不同于 Attention
传统的Attention是基于source端和target端的隐变量(hidden state)计算Attention的,得到的结果是源端(source端)的每个词与目标端(target端)每个词之间的依赖关系。
Self -Attention 首先分别在source端和target端进行自身的attention,仅与source input或者target input自身相关的Self -Attention,以捕捉source端或target端自身的词与词之间的依赖关系;然后再把source端的得到的self -Attention加入到target端得到的Attention中,称作为Cross-Attention,以捕捉source端和target端词与词之间的依赖关系。
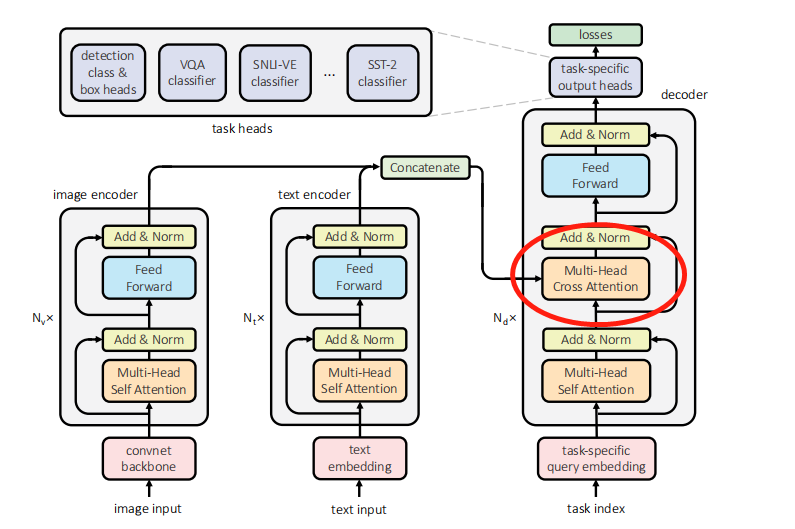
传统的Attention机制忽略了源端或目标端句子中词与词之间的依赖关系,相对比,self Attention可以不仅可以得到源端与目标端词与词之间的依赖关系,同时还可以有效获取源端或目标端自身词与词之间的依赖关系。
基本流程
关于attention有很多应用,在非seq2seq任务中,比如文本分类,或者其他分类问题,会通过self attention来使用attention。这个方法思想很简单,而且计算成本相对来说不高,强烈推荐。具体来说就是:
Query和Key,value都是相同的,即输入的句子序列信息(可以是词向量lookup后的序列信息,也可以先用cnn或者rnn进行一次序列编码后得到的处理过的序列信息。)后面的步骤与上述的都是一样的:
1、首先建立句子序列中的每个词 $q_i$ 与句子其他词 $k_i$ 的注意力权重$a_i$
2、然后将注意力权重向量进行softmax归一化,并与句子序列的所有时刻的信息(词向量或者rnn hidden state)进行线性加权。
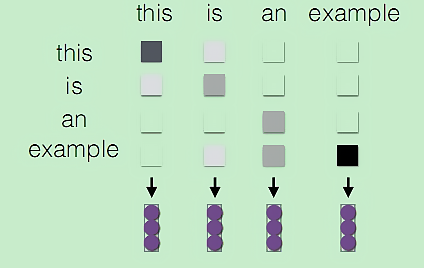
这种方法中,句子中的每个词都能与句子中任意距离的其他词建立一个敏感的关系,可以说在一定程度上提升了之前所说的CNN和RNN对于长距离语义依赖建模能力的上限。
多头注意力模型 Multi-head attention
论文 《Attention is all you need》
与原来的self-attention的核心原理其实是差不多的,但是由于self attention只从一个角度去学习关注点,可能会有点偏颇。所以,设计h种不同的$( W _ { i } ^ { Q } , W _ { i } ^ { K } , W _ { i } ^ { V } )$权重矩阵对,然后做基本的attention操作前,将query,key和value分别用上述权重对做线性变换,然后再计算得到h个不同角度的attention权重$head_i$,将这些 $head_i$按列拼接后,再与一个新的权重矩阵$W^O$做线性变换,得到最终的attention输出。
计算步骤
- 将输入单词转化成嵌入向量;
- 根据嵌入向量得到 $ q, k, v $ 三个向量;
- 为每个向量计算一个$score$: $score$ $ =q \cdot k $;
- 为了梯度的稳定, 使用归一化,即除以 $ \sqrt{d_{k}} $,($d_{k}$为特征的维度数量);
- 对score施以softmax激活函数;
- softmax点乘Value , 得到加权的每个输入向量的评分 $v$;
- 相加之后得到最终的输出结果 $ z: \quad z=\sum v 。 $
- 核心公式
$$
Attention (Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V
$$
- 以单个 self-attention 为例,词向量维度为4,单词数量2,$Q,K,V$ 维度为3,$W$ 矩阵为4$\times$3

- 其中 $Q, K, V$ 是由 $X$ 计算而来的
- 论文中计算方式如下:
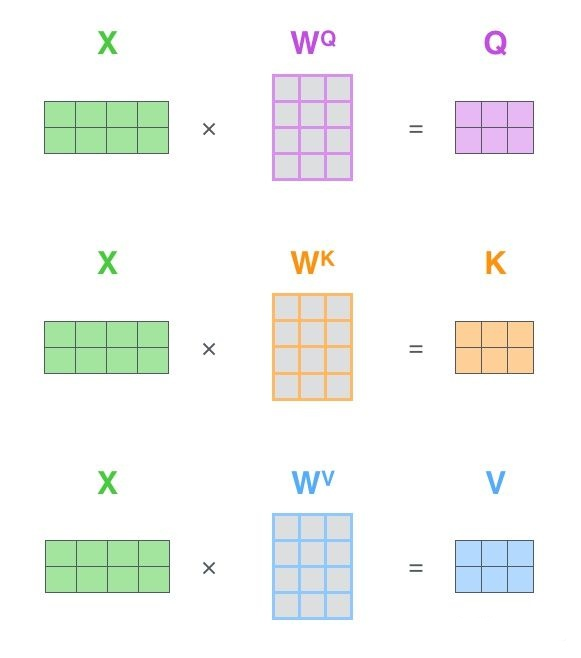
- 网络学习参数 $W^Q, Q^K, W^V$,计算得到 $Q, K, V$,维度均为 $2\times3$
- 由 $Q, K, V$ 计算得到 $Z$
- 其中$QK^T$为计算相关度的过程,得到 $2\times2$的矩阵,每行表示一组Query向量与所有Key向量的相关度
- $d_{k}$是向量维度,此处为3,$ \sqrt{d_{k}} $为归一化系数,用于防止由于维度过大导致结果太大
- softmax 按行做
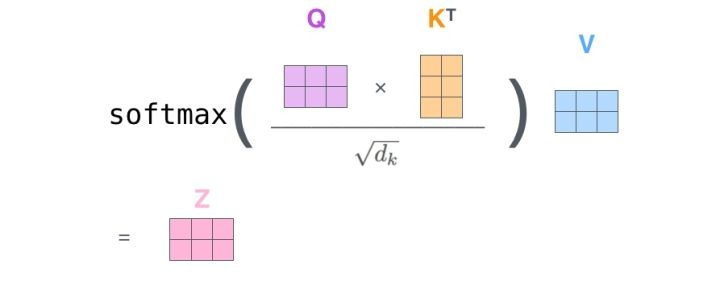
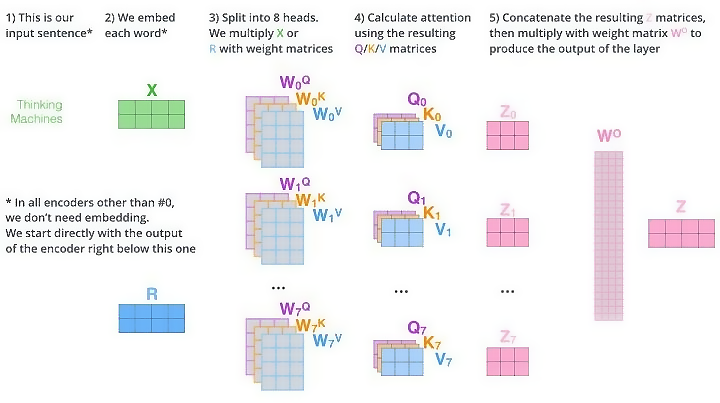
- 同一组 $X$ 输入多个 Attention模块中,得到多组 $Z_i$,将$Z_i$们连接起来组成大$Z^O$,和 $W^O$ 相乘得到输出层 $Z$
- 多头汇总,$Z$的维度是$2\times3$,8个头,共有八组$Z$,按列拼接得到 $2\times24$的特征
- 线性变化到指定维度(4),得到汇总的多头注意力结果特征$2\times4$
- 注意 Transformer 中的 Attention 会将 encoder 的 $K$ 和 $V$ 传给 decoder,而 $Q$ 来自与解码器的上一个输出。
参考资料
- https://www.cnblogs.com/gczr/p/14693829.html
- https://zhuanlan.zhihu.com/p/66076731
- https://zhuanlan.zhihu.com/p/46313756
- https://zhuanlan.zhihu.com/p/79115586
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/attention/attention/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付