1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
import torch
import numpy as np
import normflows as nf
import mtutils as mt
from matplotlib import pyplot as plt
from tqdm import tqdm
K = 16
enable_cuda = True
device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
flows = []
for i in range(K):
flows += [nf.flows.Planar((2,))]
target = nf.distributions.TwoModes(2, 0.1)
q0 = nf.distributions.DiagGaussian(2)
nfm = nf.NormalizingFlow(q0=q0, flows=flows, p=target)
nfm.to(device)
grid_size = 200
xx, yy = torch.meshgrid(torch.linspace(-3, 3, grid_size), torch.linspace(-3, 3, grid_size))
z = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
log_prob = target.log_prob(z.to(device)).to('cpu').view(*xx.shape)
prob = torch.exp(log_prob)
plt.figure(figsize=(10, 10))
plt.pcolormesh(xx, yy, prob)
plt.show()
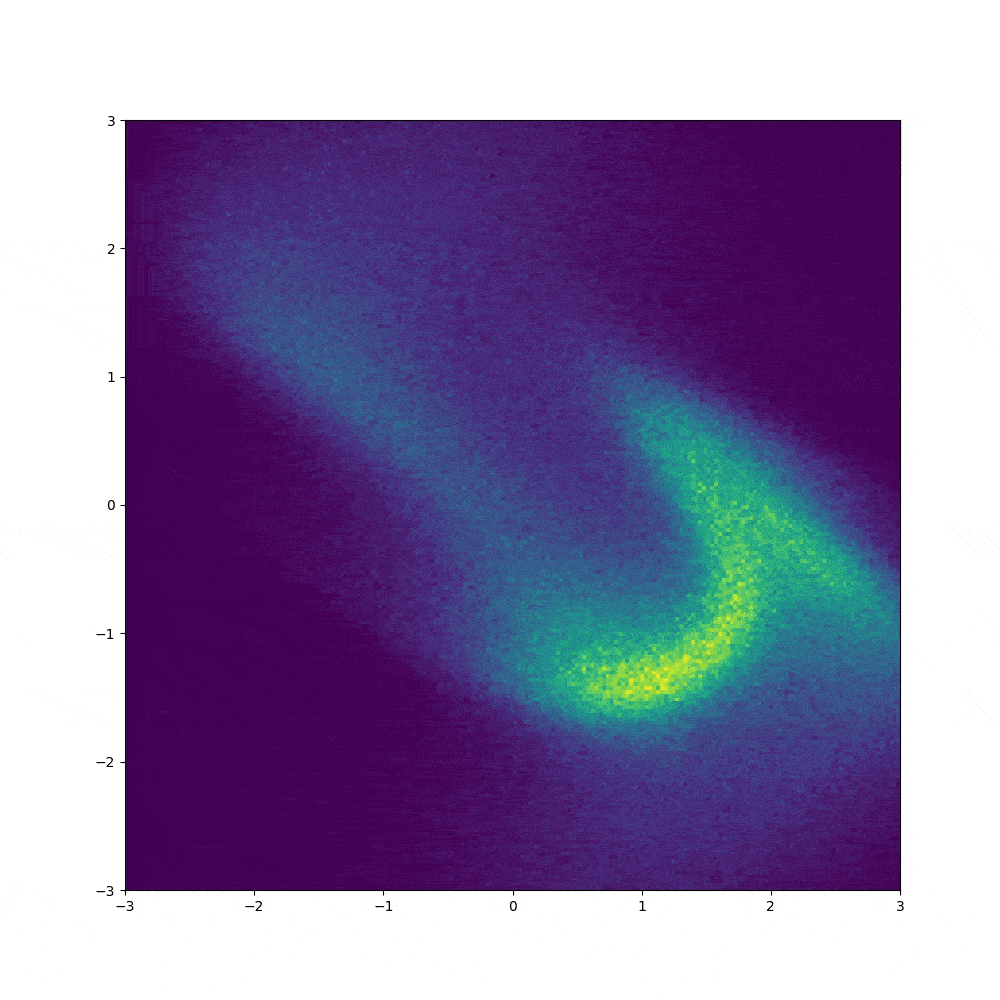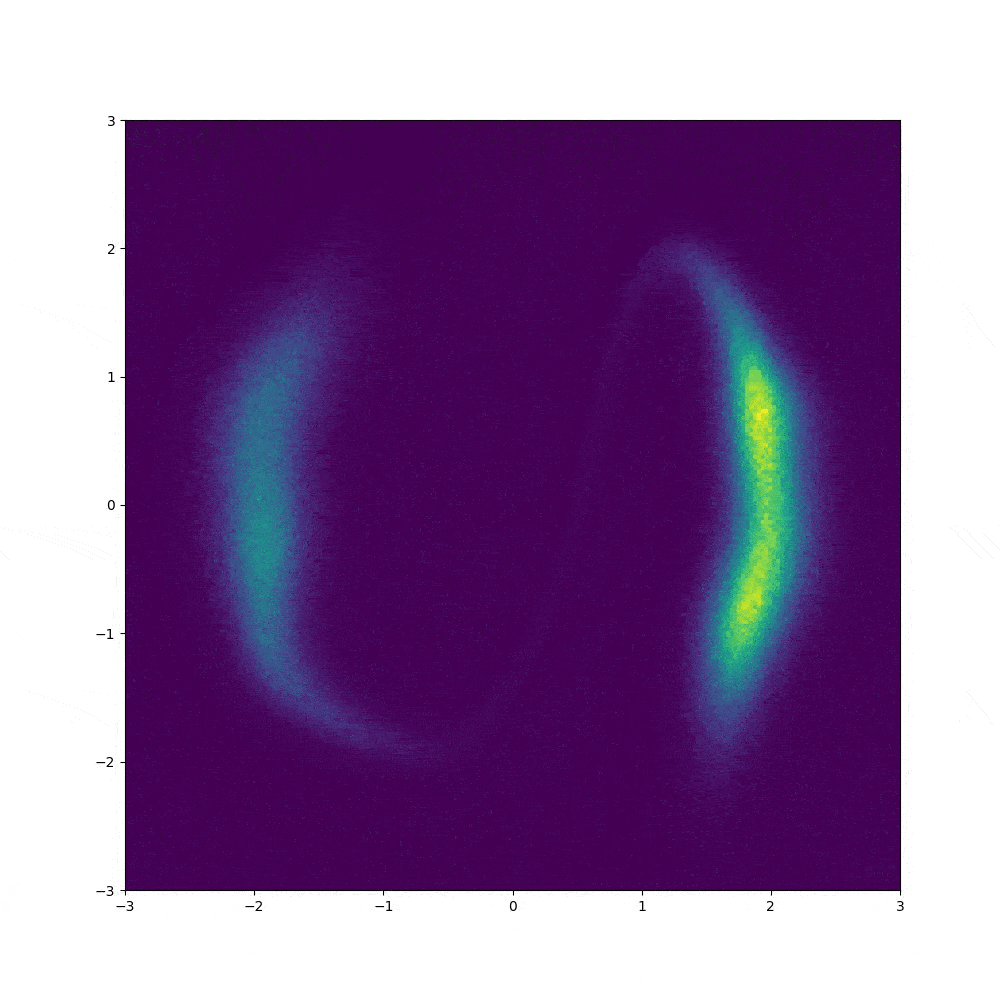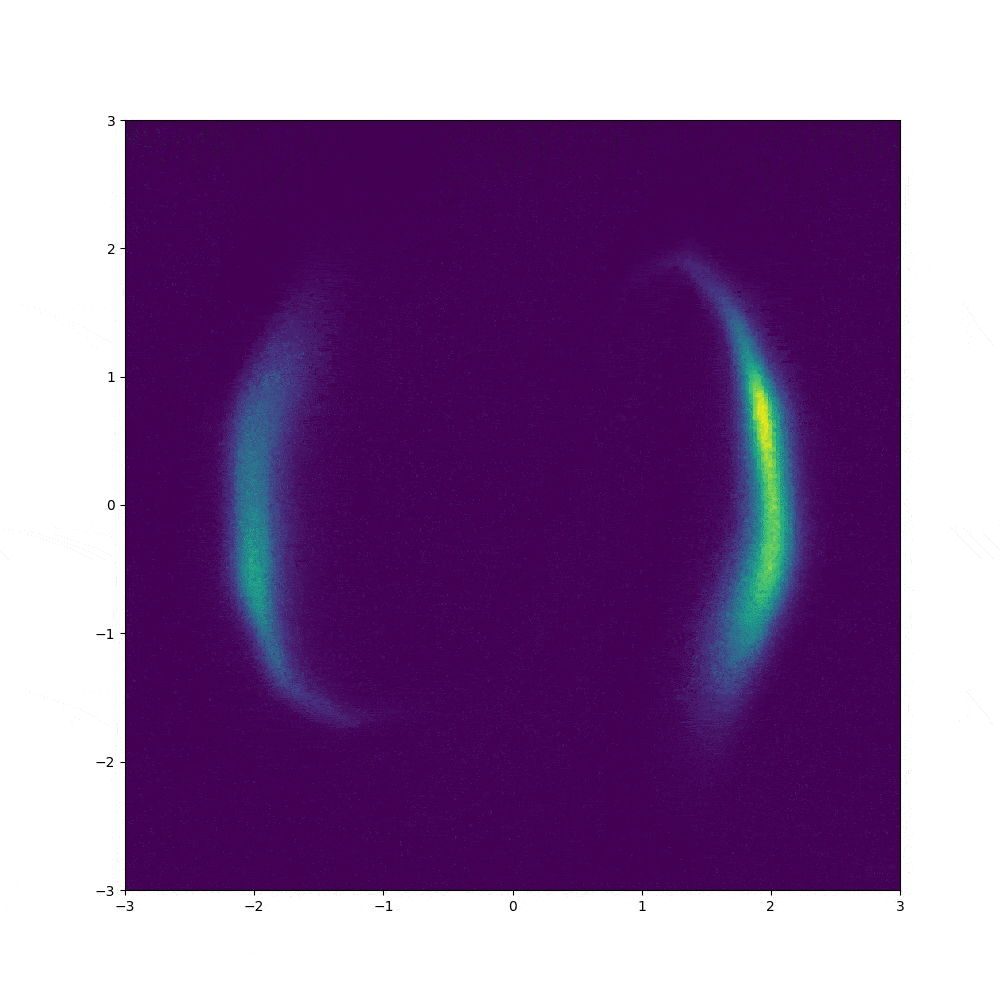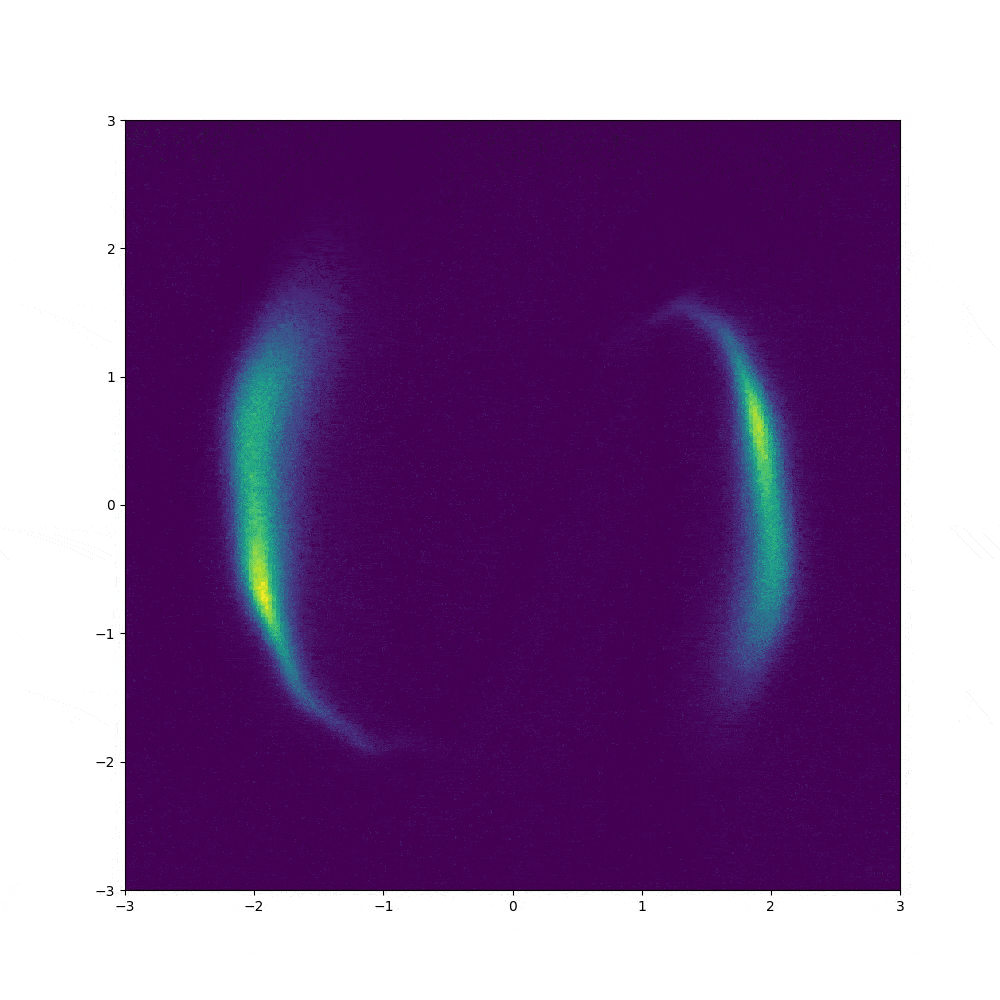
z, _ = nfm.sample(num_samples=2 ** 20)
z_np = z.to('cpu').data.numpy()
plt.figure(figsize=(10, 10))
plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (grid_size, grid_size), range=[[-3, 3], [-3, 3]])
plt.show()
max_iter = 20000
num_samples = 2 * 20
anneal_iter = 10000
annealing = True
show_iter = 200
loss_hist = np.array([])
optimizer = torch.optim.Adam(nfm.parameters(), lr=1e-3, weight_decay=1e-4)
for it in tqdm(range(max_iter)):
optimizer.zero_grad()
if annealing:
loss = nfm.reverse_kld(num_samples, beta=np.min([1., 0.01 + it / anneal_iter]))
else:
loss = nfm.reverse_kld(num_samples)
loss.backward()
optimizer.step()
loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
if (it + 1) % show_iter == 0:
torch.cuda.manual_seed(0)
z, _ = nfm.sample(num_samples=2 ** 20)
z_np = z.to('cpu').data.numpy()
plt.figure(1, figsize=(10, 10))
plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (grid_size, grid_size), range=[[-3, 3], [-3, 3]])
image = mt.convert_plt_to_rgb_image(plt)
mt.cv_rgb_imwrite(image, f"res/{it}.jpg")
z, _ = nfm.sample(num_samples=2 ** 20)
z_np = z.to('cpu').data.numpy()
plt.figure(figsize=(10, 10))
plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (grid_size, grid_size), range=[[-3, 3], [-3, 3]])
plt.show()
|