本文最后更新于:2024年5月7日 下午
学习生成模型标准化流,本文记录相关内容。
Change of variables, change of volume
简介
标准化流能把简单的地摊货概率密度(比如高斯分布)形式转换成某种高大上的分布形式。它可以用在产生式模型、强化学习、变分推断之类的地方。
Normalizing Flows尚无标准的中文译名。Flow指的是数据“流”过一系列双射(可逆映射),最终映射到合适的表征空间;Normalizing指的是,表征空间的变量积分为1,满足概率分布函数的定义。
统计机器学习
统计机器学习旨在获悉参数分布 $p(x ; \theta) $,以揭示数据的结构。以此出发,你将能达成以下四个目标:
-
采样该结构,生成数据。
这样就节省了完整的生成过程,若完整的过程纷繁浩杂,则节省巨大。同样,现实数据的维度高,采样后的低维结果就可管中窥豹,节省计算。
-
评估测试数据的似然概率。
在拒绝采样或评估模型时有用。
-
获得变量间的条件依赖关系。
如 $p\left(x_{2} \mid x_{1}\right)$ 可用来判别或回归。
这一条与上一条刚好相对应,一个是unconditional likelihood estimation,一个是conditional likelihood estimation。
-
评判算法。
如熵、互信息、高阶矩等指标,均可一试。
以上四个目标,第一个研究的最充分。合成图像、声音,已在谷歌商用。但第二三四个,研究寥寥。仅举几例,GAN的解码器,支撑集(映射到非零值的自变量)不可得;DRAW模型乃至VAE模型,概率密度不可得;哪怕已解析地了解某分布,解析的度量(如KL距离,earth-mover距离)还是不可得。
这句话说的简单点就是:深度产生式模型不容易甚至不可能进行测试和度量
即使你能合成个把接近真实数据的样本,你还离目标差得远咧!我们想要了解它们多大程度上“接近真实数据”,想要得到灵活的条件密度(如增强学习中复杂的规则),还想要在一大家子的先验分布和后验分布上做变分推断!
高斯分布
你思索片刻,想起了你的“亲密战友”高斯分布。它在你为复杂的概率分布理出头绪而焦头烂额的时候,雪中送炭:采样方便、解析的密度已知、KL距离容易计算,还有中心极限定理的保证——任何大的数据都趋近于高斯分布,所以你怎么用它几乎都对!更别提重参数化技巧啦,你还能梯度反传。这些易用的性质,让高斯分布在产生式模型和增强学习里风头无两。
不过先别高兴的太早!许多实在的场景,我们还不能用它。在增强学习里,常有连续控制机器的场景,控制规则得用多变量高斯、对角化方差矩阵(motivariate Gaussians with diagonal covariance matrices)才行呐~
相形之下,只用单模式高斯分布模型(uni-modal Gaussian distribution),在需要多模式分布(multi-modal distribution)采样的时候,乏善可陈。试举一例,要机器人绕过湖面,到达湖后的房子,规则该是二者选一:向左绕或向右绕。单模式高斯模型容不下两个规则,所以就线性地中和了它们:直直地走向湖心。糟了个糕!
高斯分布失之过简。它不能容下对立的假设;高维的情况下分布也不够集中,出现边缘效应;还不能应对罕见事物。有没有更好的分布模型,可以满足如下条件呢?
1 | |
答案是:有!你可以做这几件事。
目标分布
以下几个办法,能帮你实现需求:
- 模型融合。一个模型对付一个子任务。
- 立足当下。一次只考虑一步,让复杂的选择在此刻退化,而仅存一端。
- 非定向图模型(undirected graphical models)。
- 标准化流。你将得到一个理想的模型:可逆、可计算分布变换体积、易模拟。
下面介绍标准化流。
预备知识
为了建立直观,举例如下。让X服从均匀分布 $ \operatorname{Uniform}(0,1) , Y=f(X)=2 X+1 $ 。Y 是X的仿射变换。如下图所示。

两个方块代表概率在实数域的分布函数 $p(x)$ 和 $p(y)$,函数值代表概率密度的值。概率值的积分必须等于1,任何一个分布都是这样。所以自变量变化范围扩展为两倍后,函数值就要相应地缩减一半,从而二者面积都等于1.
也就是说,当 $X$ 水平被拉长两倍后,竖直方向上也会相应的被压缩成原来的一半。
这就是为什么模型叫标准化流,因为有加和等于1的约束
若考虑X上的极小变化 $ x+d x , \mathrm{Y} $ 相应发生变化 $ y+d y $ ,如下所示:
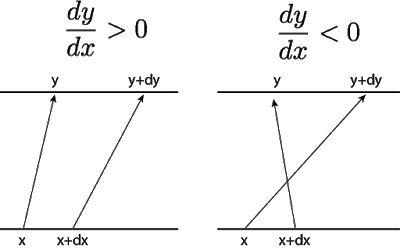
左半边的图代表一个局部增函数 $ (d y / d x>0) $ ,右边则是局部减函数 $ (d y / d x<0) $ 。
我们用微分的角度来分析。给 $ x $ 一个变化量 $ d x $ 之后, $ y $ 的变化量记为 $ d y $ 。由于要保证二者的变化量相等,$ p(x)$ 因为 $dx$ 带来的局部变化一定要等于 $ p(y)$ 随着 $dy$ 的局部变化:
$$
p(x) d x=p(y) d y
$$
为了让概率的变化守恒,我们只关心变化的量,而不关心变化的方向。(实际上,不管f(x)随着x变化增或者减,都不影响,我们假设y也做出相应的变化。)那么,我们有 :
$$
p(y)=p(x)|d x / d y|
$$
在log空间,这等价于 :
$$
\log p(y)=\log p(x)+\log |d x / d y|
$$
现在考虑多变量的例子。先考虑两个变量的情况。同上面的情况,缩放定义域中的无穷小量,我们就得到一个二维的、边长为 $dx$ 的小方块。 给这个小方块的顶点标注 $ \left(x_{1}, x_{2}, x_{3}, x_{4}\right) $ 。我们现在只关心 $ \mathrm{d} $ 相对于边长为 1 的方块的变化率。
不妨假设这个小方块就是一个边长为1的原点处的方块,那么顶点为 $ (0,0),(1,0),(0,1),(1,1) $ 。
乘以矩阵 $ [[a, b] ;[c, d]] $,我们的方块就会变成一个平行四边形,如下图。 $ (0,0) $ 还在 $ (0,0),(1,0) $ 来 到了 $ (\mathrm{a}, \mathrm{b}),(0,1) $ 被送往 $ (c, d) ,(1,1) $ 到达 $ (a+c, b+d) $ 。
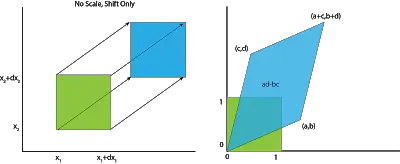
于是,一个X域边长为 1 的方块转型为平行四边形,面积大小变成了 $ a d-b c $。 这个平行四边形的面积,正是转换矩阵的行列式。 三维的情况时,“转换为平行四变形”就对应为“转换为平行六面体”,或者更高维的情况也是以此类推,“转换为平行 $n$ 维体”。行列式的道理也还是如此,线性变换后的体积,正好对应于变换矩阵的行列式。
要是转换函数f是非线性的咋办?你就不该把它简单地看作全空间的一个简单的平行体,而是对空间的每个点,对应于一个无穷小平行体。数学形式上看,局部线性变换对应的体积变化为 $ \left|\operatorname{det}\left(J\left(f^{-1}(x)\right)\right)\right| $, 这里 $ J\left(f^{-1}(x)\right) $ 代表雅各比矩阵的逆一是 $ |d x / d y| $ 的高维变种。
于是:
$$ \begin{array}{c} y=f(x) \\ p(y)=p\left(f^{-1}(y)\right) \cdot\left|\operatorname{det} J\left(f^{-1}(y)\right)\right| \\ \operatorname{logp}(y)=\log p\left(f^{-1}(y)\right)+\log \left|\operatorname{det}\left(J\left(f^{-1}(y)\right)\right)\right| \end{array} $$行列式可以被认为是变换 $ y=f(x) $ 的局部线性体积变化率。
标准化流
通过预备知识中的手段我们可以得到可逆函数的双射方法,但是为了增强模型的表达能力,我们是可以 把一系列双射连起来,在神经网络里像链子一样把它们拴在一起, 这个结构就叫“标准化流”。
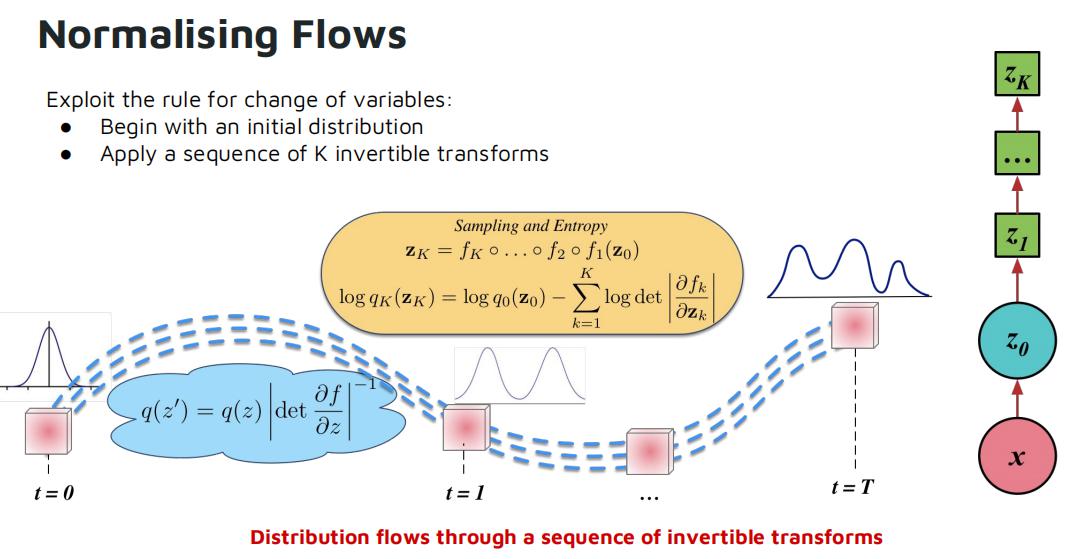
要是双射函数有可变的参数,你就可以优化这个参数,该双射就可以把基础分布转换成任意的分布。每个双射函数可以写成一个网络的层,你可以用一个优化器来学习参数,最终拟合真实数据。算法通过最大似然估计,把拟合真实数据的分布问题变成拟合变换后的概率的对数密度问题。
用对数密度的原因是为了计算的稳定性。
Normalization Flow
论文链接:https://arxiv.org/pdf/1505.05770.pdf
在variational inference中,我们通常是在优化所谓的evidence lower bound(ELBO),即:
$$ \begin{array}{l}\log p_{\theta}(\mathbf{x})=\log \int p_{\theta}(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z}) d \mathbf{z} \\ =\log \int \frac{q_{\phi}(\mathbf{z} \mid \mathbf{x})}{q_{\phi}(\mathbf{z} \mid \mathbf{x})} p_{\theta}(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z}) d \mathbf{z} \\ \geq-\mathbb{D}_{\mathrm{KL}}\left[q_{\phi}(\mathbf{z} \mid \mathbf{x}) \| p(\mathbf{z})\right]+\mathbb{E}_{q}\left[\log p_{\theta}(\mathbf{x} \mid \mathbf{z})\right]=-\mathcal{F}(\mathbf{x}),\end{array} $$最大化 $p_\theta(x) $ 需要我们找到近似于后验概率 $p_{\theta}(z \mid x) $ 的近似分布 $ q_{\phi}(z \mid x) $, 但一般的高斯分布没有办法拟合足够复杂的后验分布。 因此,NF(normalization flow)应运而生。NF用一系列的可逆映射将原始分布转换成新的分布,通过优化这一系列分布,即可实现将简单的高斯分布转换为复杂的真实后验分布的目的。
具体的,给定一个可逆映射 $ f: \mathbb{R}^{d} \rightarrow \mathbb{R}^{d} $ ,用它将随机变量 $ z \sim q(z) $ 变换为新的变量 $ z^{\prime}=f(z) $ 后,新变量的分布为:
$$
q\left(\mathbf{z}^{\prime}\right)=q(\mathbf{z})\left|\operatorname{det} \frac{\partial f^{-1}}{\partial \mathbf{z}^{\prime}}\right|=q(\mathbf{z})\left|\operatorname{det} \frac{\partial f}{\partial \mathbf{z}}\right|^{-1}
$$
第二项即是上一节中所讲的逆函数的雅克比矩阵。接着,为了构建足够复杂的分布,我们可以用多个类似的可逆映射,映射套映射:
用这样的方式,当计算转换后的分布 $q_K$ 的pdf时,不用显式地计算 $q_K$ ,而是通过初始分布 $q_0$ 的 pdf 以及映射的雅克比矩阵即可计算。而一般函数的雅克比矩阵的计算复杂度达到了 $ O\left(D^{3}\right) $ ,在 NF 的应用中显然不可行。因此,NF需要找到雅克比矩阵可以被高效运算的可逆映射函数。
在原文中,作者给出了两种映射函数的选择,分别是:
-
Planar Flow
$$ \begin{array}{c}\psi(\mathbf{z})=h^{\prime}\left(\mathbf{w}^{\top} \mathbf{z}+b\right) \mathbf{w} \\ \left|\operatorname{det} \frac{\partial f}{\partial \mathbf{Z}}\right|=\left|\operatorname{det}\left(\mathbf{I}+\mathbf{u} \psi(\mathbf{z})^{\top}\right)\right|=\left|1+\mathbf{u}^{\top} \psi(\mathbf{z})\right|\end{array} $$
$$
f(\mathbf{z})=\mathbf{z}+\mathbf{u} h\left(\mathbf{w}^{\top} \mathbf{z}+b\right)
$$
其中, $ w, u, b $ 是要学习的参数, $ h(\cdot) $ 是element-wise的非线性变换。该映射的雅克比可以在 $ O(D) $ 的时间复杂度内计算 : -
Radial Flow
$$ \begin{array}{l}f(\mathbf{z})=\mathbf{z}+\beta h(\alpha, r)\left(\mathbf{z}-\mathbf{z}_{0}\right) \\ \left.\left|\operatorname{det} \frac{\partial f}{\partial \mathbf{z}}\right|=[1+\beta h(\alpha, r)]^{d-1}\left[1+\beta h(\alpha, r)+\beta h^{\prime}(\alpha, r) r\right)\right]\end{array} $$
Planar flow和radial flow分别是在平面空间和球形空间中对原分布进行变换。下图形象的表示了NF的不同长度(也可以叫层数)K与最终分布的关系。

这两种简单的映射函数只适用于低维的情况,为了处理高维的依赖,Autoregressive Flows(自回归流)是一种合适的选择。
Autoregressive Flows
关于自回归流,有三篇比较经典的文章,包括 Real-NVP,MAF和IAF。这里先讲Real-NVP和IAF。 MAF和IAF想法是镜像的,就不赘述了。
需要说明的是,所有自回归流的模型都是建立在这样的一条理论基础上的:三角矩阵的行列式是其对角元素的乘积。形式上,第 $ i $ 维的变量 $ x_{i} $ 的生成只依赖于之前生成的变量 $ x_{1: i-1} $ ,即 :
$$ \begin{aligned} p\left(x_{i} \mid x_{1: i-1}\right) & =\mathcal{N}\left(x_{i} \mid \mu_{i},\left(\exp \alpha_{i}\right)^{2}\right) \\ \mu_{i} & =f_{\mu_{i}}\left(x_{1: i-1}\right) \\ \alpha_{i} & =f_{\alpha_{i}}\left(x_{1: i-1}\right)\end{aligned} $$Real-NVP
这篇文章引入了 affine coupling layer ( 仿射耦合层) 的概念。给定一个 $ D $ 维的输入 $ x $ , $ d<D $ ,则该层的输出 $ y $ 如下计算 :
$$ \begin{aligned} y_{1: d} & =x_{1: d} \\ y_{d+1: D} & =x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right), \end{aligned} $$$s$ 和 $t$ 分别对应上面的 $ \alpha $ 和 $ \mu $。也就是说,Real-NVP将输入的一部分维度保持不变,而另一部分 维度进行变换。这样得到的映射函数的雅克比矩阵为 :
$$ \frac{\partial y}{\partial x^{T}}=\left[\begin{array}{cc} \mathbb{I}_{d} & 0 \\ \frac{\partial y_{d+1: D}}{\partial x_{1: d}^{T}} & \operatorname{diag}\left(\exp \left[s\left(x_{1: d}\right)\right]\right) \end{array}\right] $$它的行列式可以被简单的计算 : $ \exp \left[\sum_{j} s\left(x_{1: d}\right)_{j}\right] $ 。并且由于计算行列式的过程不依赖于 $ s $ 或 $ t $ 的行列式,所以可以选取任意复杂的函数作为 $ s $ 和 $ t $ 。
此外,这样的映射函数还有一个性质,即它的逆映射的计算复杂度和正向的计算复杂度相等:
$$ \begin{array}{c}\left\{\begin{array}{ll}y_{1: d} & =x_{1: d} \\ y_{d+1: D}=x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right)\end{array}\right. \\ \Leftrightarrow\left\{\begin{array}{l}x_{1: d}=y_{1: d} \\ x_{d+1: D}=\left(y_{d+1: D}-t\left(y_{1: d}\right)\right) \odot \exp \left(-s\left(y_{1: d}\right)\right),\end{array}\right.\end{array} $$也就是说,sampling和inference的时间复杂度相等,而且由于逆映射的计算也不依赖于 $s$ 和 $t$ 的逆,所以其函数的选择可以任意复杂。
可以看出来,一层affine coupling layer只能变换输入的部分维度,要想实现对整体的变换,可以将多层affine coupling layer堆叠起来。同时,用一个二元的mask $b$ ,即可高效的实现该层的计算:
$$
y=b \odot x+(1-b) \odot(x \odot \exp (s(b \odot x))+t(b \odot x))
$$
但在实验中,Real-NVP的效果并没有IAF和MAF好。
IAF
Autoregressive Flow 的 sampling 过程如下: 首先随机sample一个橾声 $ \epsilon \sim N(0, I) $ ,其对应的变量 $ x_{0}=\mu_{0}+\sigma_{0} \odot \epsilon_{0} $ ,对于 $ i>1 , x_{i}=\mu_{i}\left(x_{1: i-1}\right)+\sigma_{i}\left(x_{1: i-1}\right) \cdot \epsilon_{i} $ 。显然这个过程是没有办法并行的,sample 时速度很慢。IAF 可以看做是上式的 reparametrisation,即:
$$
x_{i}=\mu_{i}\left(z_{1: i-1}\right)+\sigma_{i}\left(z_{1: i-1}\right) \cdot z_{i}
$$
其中, $ z \sim q(z) $ 。由于上式中 $ x_{i} $ 的计算不依赖于之前生成的 $ x_{1: i-1} $ ,因此可以被并行的计算:
$$
x=\mu(z)+\sigma(z) \circ z
$$
也就是说,在sampling的时候,IAF可以被高效的并行。但是在inference的时候,想要得到 $ z_{i} $ ,还是需要根据 $ z_{i}=\mu_{i}+\sigma_{i} \odot z_{i-1} $ 依次计算,所以在训练过程中,IAF是比较慢的。
相反的,MAF在训练时快,sample时慢。Parallel-Wavenet实现了两者的结合,用MAF作为teacher model,负责训练时提供分布的指导信息;而用IAF作为student model,负责最终的sample。这个基于knowledge distillation的方法在语音合成上取得了很好的效果,同时也保证了生成语音的速度。
WaveGlow and FloWavenet
这里再介绍一下Normalization Flow在语音合成上比较新的工作。WaveGlow和FlowWavenet的模型基本相同,也是同时放出来的,这里按照WaveGlow的模型进行介绍。流程图如下:
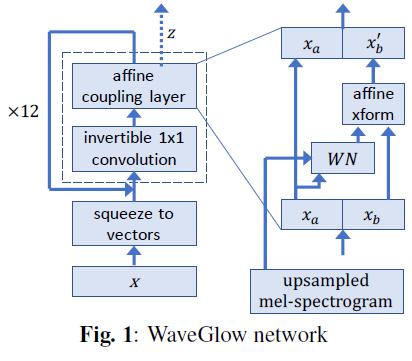
WaveGlow引入了Real-NVP中的affine coupling layer,每一次对输入向量的一半维度进行变换,另一半保持不变。上图右侧的转换过程可以表示为:
$$ \begin{array}{c}x_{a}, x_{b}=\operatorname{split}(x) \\ (\log s, t)=W N\left(x_{a}, \text { mel-spectrogram }\right) \\ x_{b} \prime=\boldsymbol{s} \odot x_{b}+t \\ f_{\text {coupling }}^{-1}(x)=\operatorname{concat}\left(x_{a}, x_{b} \prime\right)\end{array} $$其中, $ x_{a} $ 和 $ x_{b} $ 是将 $ x $ 等分的结果,FlowWavenet中是按照索引的奇偶来分的。 $ W N(\cdot) $ 是任 意的变换函数,两篇文章均用的non-causal Wavenet,也可以说是non-autoregressive的wavenet。该变换的雅克比矩阵的行列式为:
$$
\log \left|\operatorname{det}\left(\boldsymbol{J}\left(\boldsymbol{f}_{\text {coupling }}^{-1}(\boldsymbol{x})\right)\right)\right|=\log |\boldsymbol{s}|
$$
前面提到过,Real-NVP每一层只能变换一部分的输入。为了实现完整的变换,WaveGlow引入了与Glow[10]中相似的1x1 Invertible Convolution,因为还没看过Glow,所以先留作一个坑。FlowWavenet中,作者则简单的交换了输入向量奇偶索引上的元素来实现这一目的。此外,两个模型还有一些微小的差异,但motivation和idea都是一样的。
损失函数
标准化流网络的训练通常使用最大化对数似然作为损失函数。具体来说,损失函数关注于以下两个方面:
- 数据的对数似然:
- 损失函数旨在最大化转换后数据在简单分布(如高斯分布)下的对数似然。这意味着网络学习如何将数据有效地映射到这个简单分布上。
- 雅可比行列式的计算:
- 由于变换是可逆的,损失函数还包括计算变换的雅可比行列式(Jacobian determinant),以确保变换的正确性和可逆性。
数学表达
损失函数可以表达为:
$$
\mathcal{L}=-\sum_{i=1}^N(\log p_Z(f_\theta(x_i))+\log|\det J_{f_\theta}(x_i)|)
$$
其中,$f_{\theta}$ 是网络变换,$x_i$ 是原始数据点,$p_Z$ 是目标分布 (如标准高斯分布) , $J_{f_\theta}$ 是变换的雅可比矩阵,$N$ 是数据点的数量。
通过优化这个损失函数,标准化流网络学习如何将复杂的数据分布映射到一个简单的、可管理的分布上。这种方法在各种场景中被用于概率建模和生成任务,如图像生成、语音合成等。
步骤解析
- 应用变换:首先,输入数据 $x$ 通过网络的一系列可逆变换 $f_{\theta}$ 被映射到新的空间。这里$\theta$ 表示网络的参数。
- 计算目标分布下的概率密度:浮映射后的数据 $z=f_o(x)$ 放入目标分布的概率密度函数中。在标准化流网络中,目标分布通常是一个标准的多维高斯分布,其概率密度函数为$p_{Z}(z)_{\circ}$
- 对数似然计算:计算每个映射后的数据点在目标分布下的对数似然。对数似然是概率密度的自然对数,即$\log p_Z(z)$。
具体计算
如果目标分布是一个标准多维高斯分布,其概率密度函数可以表示为:
$$
p_Z(z)=\frac1{(2\pi){d/2}}\exp\left(-\frac12zTz\right)
$$
其中,$d$ 是数据的维度,$z^Tz$是$z$ 的内积,即映射后数据点的平方和。
因此,对数似然$\log p_Z(z)$ 可以计算为 :
$$
\log p_Z(z)=-\frac d2\log(2\pi)-\frac12z^Tz
$$
在实践中,通常会对整个数据集的所有数据点计算对数似然的平均值,以作为损失函数的一部分。
注意
- 在实际计算中,为了避免数值计算问题(如下溢或上溢),可能需要特别处理对数似然的计算。
- 这一计算步骤是损失函数的关键组成部分,它确保了变换后的数据能够符合目标分布的形状,从而学习到一个有效的数据表示。
通过这种方法,标准化流网络能够学习将数据从其原始复杂分布映射到一个简单且标准化的分布,如多维高斯分布,同时保持变换的可逆性。
原始论文
### 参考资料- Rezende D, Mohamed S. Variational inference with normalizing flows[C]//International conference on machine learning. PMLR, 2015: 1530-1538.
- https://blog.evjang.com/2018/01/nf1.html
- https://www.jianshu.com/p/66393cebe8ba
- https://zhuanlan.zhihu.com/p/59615785
- https://www.youtube.com/watch?v=JrO5fSskISY
- https://www.shakirm.com/slides/DeepGenModelsTutorial.pdf
文章链接:
https://www.zywvvd.com/notes/study/deep-learning/generation/normalizing-flows/normalizing-flow/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付