KD-树 - 又见苍岚

本文最后更新于：2024年9月19日上午

KD-树(k-dimensional tree)是一种用于组织点在k维空间中的数据结构，主要用于各种搜索和优化任务，如最近邻搜索、范围搜索和k最近邻搜索。KD-树是二叉树的一种特殊形式，可以看作是二分搜索树(BST)的推广，但适用于多个维度。本文记录相关内容。

简介

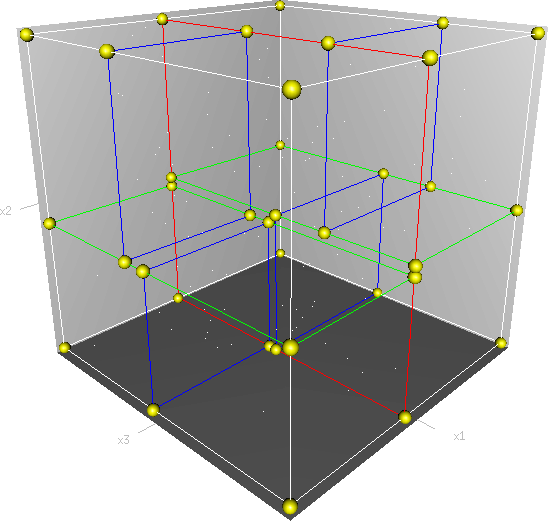
kd树(k-dimensional树的简称)，是一种分割k维数据空间的数据结构，其中的每一个节点都是k维的数据，主要应用于多维空间关键数据的近邻查找(Nearest Neighbor)和近似最近邻查找(Approximate Nearest Neighbor)。

其实KDTree就是二叉查找树(Binary Search Tree，BST)的变种。二叉查找树的性质如下：

若它的左子树不为空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树；

如果我们要处理的对象集合是一个K维空间中的数据集，我们首先需要确定是：怎样将一个K维数据划分到左子树或右子树？

在构造1维BST树类似，只不过对于Kd树，在当前节点的比较并不是通过对K维数据进行整体的比较，而是选择某一个维度d，然后比较两个K维数据在该维度 d上的大小关系，即每次选择一个维度d来对K维数据进行划分，相当于用一个垂直于该维度d的超平面将K维数据空间一分为二，平面一边的所有K维数据在d维度上的值小于平面另一边的所有K维数据对应维度上的值。也就是说，我们每选择一个维度进行如上的划分，就会将K维数据空间划分为两个部分，如果我们继续分别对这两个子K维空间进行如上的划分，又会得到新的子空间，对新的子空间又继续划分，重复以上过程直到每个子空间都不能再划分为止。以上就是构造 Kd-Tree的过程，上述过程中涉及到两个重要的问题：

每次对子空间的划分时，怎样确定在哪个维度上进行划分；
在某个维度上进行划分时，怎样确保建立的树尽量地平衡，树越平衡代表着分割得越平均，搜索的时间也就是越少。

1、在哪个维度上进行划分？

一种选取轴点的策略是 median of the most spread dimension pivoting strategy，统计样本在每个维度上的数据方差，挑选出对应方差最大值的那个维度。数据方差大说明沿该坐标轴方向上数据点分散的比较开。这个方向上，进行数据分割可以获得最好的平衡。

2、怎样确保建立的树尽量地平衡？

给定一个数组，怎样才能得到两个子数组，这两个数组包含的元素个数差不多且其中一个子数组中的元素值都小于另一个子数组呢？方法很简单，找到数组中的中值(即中位数，median)，然后将数组中所有元素与中值进行比较，就可以得到上述两个子数组。同样，在维度d上进行划分时，划分点(pivot)就选择该维度d上所有数据的中值，这样得到的两个子集合数据个数就基本相同了。

构建 Kd-Tree

在K维数据集合中选择具有最大方差的维度k，然后在该维度上选择中值m为pivot对该数据集合进行划分，得到两个子集合；同时创建一个树结点node，用于存储；
对两个子集合重复(1)步骤的过程，直至所有子集合都不能再划分为止；

示例

假设有 6 个二维数据点 ${(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}$，数据点位于二维空间内(如下图中黑点所示)。

kd树算法就是要确定图中这些分割空间的分割线(多维空间即为分割平面，一般为超平面)。下面就要通过一步步展示kd树是如何确定这些分割线的。

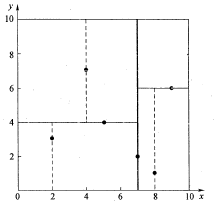
分别计算x，y方向上数据的方差，得知x方向上的方差最大；
根据x轴方向的值2,5,9,4,8,7排序选出中值为7，所以该node中的data = (7,2)。这样，该节点的分割超平面就是通过(7,2)并垂直于x轴的直线x = 7；
确定左子空间和右子空间。分割超平面x = 7将整个空间分为两部分，如下图所示。x < = 7的部分为左子空间，包含3个节点{(2,3)，(5,4)，(4,7)}；另一部分为右子空间，包含2个节点{(9,6)，(8,1)}。

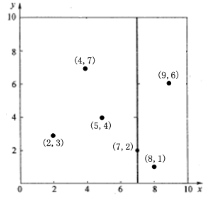
更新分割轴：一共就两个维度，所以，下一个维度是y轴。
确定子节点：

左节点：在左支中找到y轴的中位数 (5,4)，左支数据更新为{(2,3)}，右支数据更新为{(4,7)}

右节点：在右支中找到y轴的中位数 (9,6)，左支数据更新为{(8,1)}，右支数据为null。
更新分割轴：下一个维度为x轴。
确定(5,4)的子节点：

左节点：由于只有一个数据，所以，左节点为 (2,3)

右节点：由于只有一个数据，所以，右节点为 (4,7)
确定 (9,6) 的子节点：

左节点：由于只有一个数据，所以，左节点为 (8,1)

右节点：右节点为空。

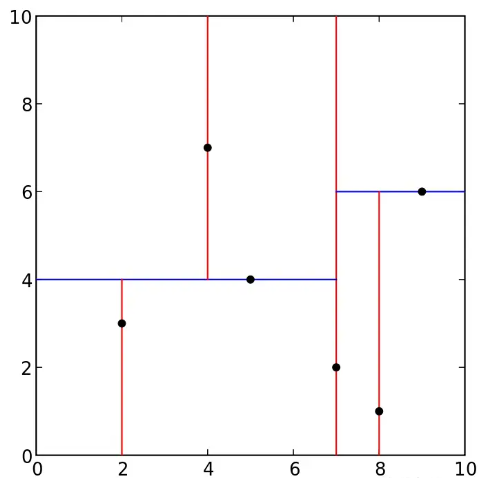
kd-tree表示：

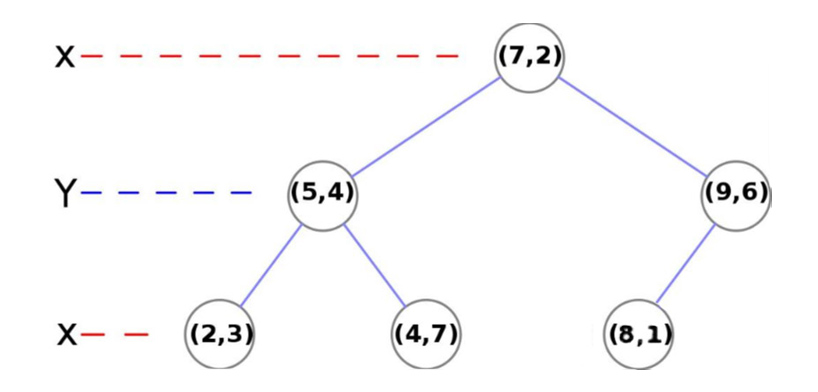
Kd-Tree 最近邻查找

在构建了完整的kd-tree之后，我们想要使用他来进行高维空间的检索。

将查询数据Q从根结点开始，按照Q与各个结点的比较结果向下访问Kd-Tree，直至达到叶子结点。
其中Q与结点的比较指的是将Q对应于结点中的k维度上的值与中值m进行比较，若Q(k) < m，则访问左子树，否则访问右子树。达到叶子结点时，计算Q与叶子结点上保存的数据之间的距离，记录下最小距离对应的数据点，记为当前最近邻点nearest和最小距离dis。
进行回溯操作，该操作是为了找到离Q更近的“最近邻点”。即判断未被访问过的分支里是否还有离Q更近的点，它们之间的距离小于dis。
如果Q与其父结点下的未被访问过的分支之间的距离小于dis，则认为该分支中存在离P更近的数据，进入该结点，进行(1)步骤一样的查找过程，如果找到更近的数据点，则更新为当前的最近邻点nearest，并更新dis。

如果Q与其父结点下的未被访问过的分支之间的距离大于dis，则说明该分支内不存在与Q更近的点。
回溯的判断过程是从下往上进行的，直到回溯到根结点时已经不存在与P更近的分支为止。

注：判断未被访问过的树分支中是否还有离Q更近的点，就是判断"Q与未被访问的树分支的距离|Q(k) - m|“是否小于"Q到当前的最近邻点nearest的距离dis”。从几何空间上来看，就是判断以Q为中心，以dis为半径超球面是否与未被访问的树分支代表的超矩形相交。

下面举两个例子来演示一下最近邻查找的过程。
假设我们的kd树就是上面通过样本集{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}创建的。

例一

查找 (2.1,3.1) 的最近邻。

如下图所示，红色的点即为要查找的点。通过二叉搜索，顺着搜索路径很快就能找到当前的最邻近点(2,3)。

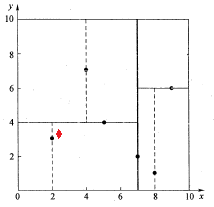
在上述搜索过程中，产生的搜索路径节点有<(7,2)，(5,4)，(2,3)>。为了找到真正的最近邻，还需要进行’回溯’操作，首先以(2,3)作为当前最近邻点nearest，计算其到查询点Q(2.1,3.1)的距离dis为0.1414，然后回溯到其父节点(5,4)，并判断在该父节点的其他子节点空间中是否有距离查询点Q更近的数据点。以(2.1,3.1)为圆心，以0.1414为半径画圆，如图所示。发现该圆并不和超平面y = 4交割，即这里：|Q(k) - m|=|3.1 - 4|=0.9 > 0.1414，因此不用进入(5,4)节点右子空间中去搜索。

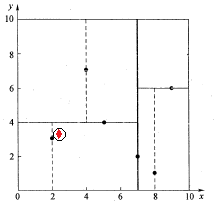
再回溯到(7,2)，以(2.1,3.1)为圆心，以0.1414为半径的圆更不会与x = 7超平面交割，因此不用进入(7,2)右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点(2,3)，最近距离为0.1414。

例二

查找点Q(2,4.5)

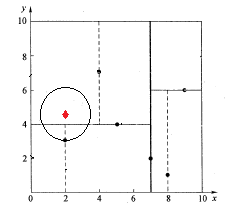
如下图所示，同样经过二叉搜索，可得当前的最邻近点(4,7)，产生的搜索路径节点有<(7,2)，(5,4)，(4,7)>。首先以(4,7)作为当前最近邻点nearest，计算其到查询点Q(2,4.5)的距离dis为3.202，然后回溯到其父节点(5,4)，并判断在该父节点的其他子节点空间中是否有距离查询点Q更近的数据点。以(2,4.5)为圆心，以为3.202为半径画圆，如图所示。发现该圆和超平面y = 4交割，即这里：|Q(k) - m|=|4.5 - 4|=0.5 < 3.202，因此进入(5,4)节点右子空间中去搜索。所以，将(2,3)加入到搜索路径中，现在搜索路径节点有<(7,2), (2, 3)>。同时，注意：点Q(2,4.5)与父节点(5,4)的距离也要考虑，由于这两点间的距离3.04 < 3.202，所以将(5,4)赋给nearest，并且dist=3.04。

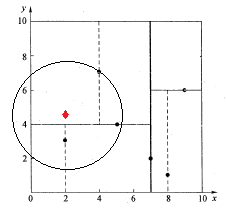
接下来，回溯至(2,3)叶子节点，点Q(2,4.5)和(2,3)的距离为1.5，比距离(5,4)要近，所以最近邻点nearest更新为(2,3)，最近距离dis更新为1.5。回溯至(7,2)，如图所示，以(2,4.5)为圆心1.5为半径作圆，并不和x = 7分割超平面交割，即这里：|Q(k) - m|=|2 - 7|=5 > 1.5。至此，搜索路径回溯完。返回最近邻点(2,3)，最近距离1.5。

Kd树在维度较小时(比如20、30)，算法的查找效率很高，然而当数据维度增大(例如：K≥100)，查找效率会随着维度的增加而迅速下降。假设数据集的维数为D，一般来说要求数据的规模N满足N>>2的D次方，才能达到高效的搜索。

为了能够让Kd树满足对高维数据的索引，Jeffrey S. Beis和David G. Lowe提出了一种改进算法——Kd-tree with BBF(Best Bin First)，该算法能够实现近似K近邻的快速搜索，在保证一定查找精度的前提下使得查找速度较快。

Python 实现

Python scipy.spatial 包中封装了 KDTree 的实现

1	`class KDTree(data, leafsize=10, compact_nodes=True, copy_data=False, balanced_tree=True, boxsize=None)`

Parameters:

data array_like, shape (n,m)

The n data points of dimension m to be indexed. This array is not copied unless this is necessary to produce a contiguous array of doubles, and so modifying this data will result in bogus results. The data are also copied if the kd-tree is built with copy_data=True.

leafsize positive int, optional

The number of points at which the algorithm switches over to brute-force. Default: 10.

compact_nodes bool, optional

If True, the kd-tree is built to shrink the hyperrectangles to the actual data range. This usually gives a more compact tree that is robust against degenerated input data and gives faster queries at the expense of longer build time. Default: True.

**copy_data **bool, optional

If True the data is always copied to protect the kd-tree against data corruption. Default: False.

**balanced_tree **bool, optional

If True, the median is used to split the hyperrectangles instead of the midpoint. This usually gives a more compact tree and faster queries at the expense of longer build time. Default: True.

**boxsize **array_like or scalar, optional

Apply a m-d toroidal topology to the KDTree… The topology is generated by 𝑥𝑖+𝑛𝑖𝐿𝑖 where 𝑛𝑖 are integers and 𝐿𝑖 is the boxsize along i-th dimension. The input data shall be wrapped into [0,𝐿𝑖). A ValueError is raised if any of the data is outside of this bound.
Attributes:

data ndarray, shape (n,m)

The n data points of dimension m to be indexed. This array is not copied unless this is necessary to produce a contiguous array of doubles. The data are also copied if the kd-tree is built with copy_data=True.

leafsize positive int

The number of points at which the algorithm switches over to brute-force.

m int

The dimension of a single data-point.

n int

The number of data points.

maxes ndarray, shape (m,)

The maximum value in each dimension of the n data points.

mins ndarray, shape (m,)

The minimum value in each dimension of the n data points.

size int

The number of nodes in the tree.
Methods

`count_neighbors`(other, r[, p, weights, …])	Count how many nearby pairs can be formed.
`query`(x[, k, eps, p, distance_upper_bound, …])	Query the kd-tree for nearest neighbors.
`query_ball_point`(x, r[, p, eps, workers, …])	Find all points within distance r of point(s) x.
`query_ball_tree`(other, r[, p, eps])	Find all pairs of points between self and other whose distance is at most r.
`query_pairs`(r[, p, eps, output_type])	Find all pairs of points in self whose distance is at most r.
`sparse_distance_matrix`(other, max_distance)	Compute a sparse distance matrix.

示例代码

from scipy.spatial import KDTree


if __name__ == "__main__":
    # Create a KDTree
    points = [(1, 2), (3, 4), (5, 6), (7, 8)]
    kdtree = KDTree(points)

    # Query the KDTree
    query_point = (4, 4.5)
    result = kdtree.query(query_point)

    print("The nearest neighbor of", query_point, "is", points[result[1]])