贝塞尔曲线

本文最后更新于：2024年9月19日上午

应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，如 Photoshop 中的钢笔工具，本文记录相关内容。

简介

贝塞尔曲线 (Bézier Curve) 是由法国工程师皮埃尔·贝兹 (Pierre Bézier) 于 1962 年所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计 1。贝塞尔曲线最初由保尔·德·卡斯特里奥 (Paul de Casteljau) 于 1959 年运用德卡斯特里奥算法 (De Casteljau’s Algorithm) 开发，以稳定数值的方法求出贝塞尔曲线。

贝塞尔曲线

线性贝塞尔曲线

给定点 $P_0,P_1$，线性贝塞尔曲线定义为：
$$
B \left(t\right) = \left(1 - t\right) P_0 + t P_1, t \in \left[0, 1\right]
$$
不难看出，线性贝塞尔曲线即为点 $P_0$ 和 $P_1$ 之间的线段。整个线性贝塞尔曲线生成过程如下图所示：

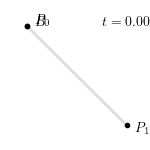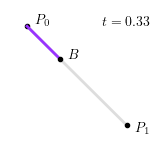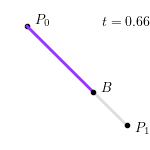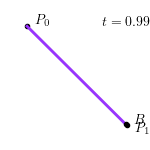
二阶贝塞尔曲线

给定点 $P_0, P_1, P_2$，二次贝塞尔曲线定义为：
$$
B \left(t\right) = \left(1 - t\right)^2 P_0 + 2 t \left(1 - t\right) P_1 + t^2 P_2, t \in \left[0, 1\right]
$$
二次贝塞尔曲线生成过程如下图所示：

三阶贝塞尔曲线

给定点 $P_0, P_1, P_2, P_3$ ，三次贝塞尔曲线定义为：
$$
B \left(t\right) = \left(1 - t\right)^3 P_0 + 3 t \left(1 - t\right)^2 P_1 + 3 t^2 \left(1 - t\right) P_2 + t^3 P_3, t \in \left[0, 1\right]
$$
三次贝塞尔曲线生成过程如下图所示：

测试曲线

三阶贝塞尔曲线

一般化的贝塞尔曲线

对于一般化的贝塞尔曲线，给定点 $P_0, P_1, \cdots, P_n$ , n 阶贝塞尔曲线定义为：
$$
B \left(t\right) = \sum_{i=0}^{n}{\binom{n}{i} \left(1 - t\right)^{n - i} t^{i} P_i}, t \in \left[0, 1\right]
$$
其中
$$
b_{i, n} \left(t\right) = \binom{n}{i} \left(1 - t\right)^{n - i} t^{i}
$$
称之为 n 阶 Bernstein 多项式，点 $P_i$ 称为贝塞尔曲线的控制点。

可以认为贝塞尔曲线就是多个控制点之间连成的线段上，递归实现的线性变化。

贝塞尔曲线的绘制

通过前面的介绍，也就是说我们的贝塞尔曲线可以通过一堆控制点来画出，那么假如我们有如下三个控制点，我们怎么来画出一个贝塞尔曲线呢？

贝塞尔曲线参数形式的表达，是对曲线上各个点坐标的表达，那么我们只需要根据这些控制点依照 t 的变换求出对应的点，即可求出曲线上所有的点，从而形成曲线。

那么问题就变成了我知道控制点和 t 的值，求曲线上对应的点 P(t) 的坐标是多少。这个问题我们可以使用德卡斯特里奥算法（de Casteljau Algorithm）来解决。

我们先把 $ P_{0}, P_{1}, P_{2} \ldots P_{n} $ 连线，例子中就三个点，连线如下：

通过线性插值在线段上找到中间点 $P_{0,1}$，使得 $ P_{0} P_{0,1}: P_{0,1} P 1=t: 1-t $ ，其他线段也如此，我们就可得到下图

然后我们连接 $ P_{0,1} P_{1,1} $ ，得到新的线段，然后在该线段上再取一点使得该线段被分为 t 和 1-t，那么就会得到下图：

如果有更多的控制点，我们也可以使用相同的方法来求出曲线上的一点，如下图是四个控制点求曲线上一点的过程：

伯恩斯坦多项式与de Casteljau算法

拿最简单的二阶贝塞尔曲线举例，如下图：

图中蓝色的点为控制点，他们的坐标我们是知道的，那么通过线性插值，我们可以得到求出红色点的坐标:
$$
\begin{array}{l}P_{0}^{1}=(1-t) P_{0}+t P_{1} \ P_{1}^{1}=(1-t) P_{1}+t P_{2}\end{array}
$$
红色点坐标求出后，我们自然可以再求出绿色点的坐标：
$$
P_{0}^{2}=(1-t) P_{0}^{1}+t P_{1}^{1}
$$
把上面两个式子带入到下面的式子，得到：
$$
\begin{array}{l}P_{0}^{2}=(1-t)\left((1-t) P_{0}+t P_{1}\right)+t\left((1-t) P_{1}+t P_{2}\right) \ =(1-t)^{2} P_{0}+2 t(1-t) P_{1}+t^{2} P_{2}\end{array}
$$
我们还可以用这个方法去算三阶的，四阶的，乃至n阶的贝塞尔曲线，得到的结果为曲线上任意一点P(t)是各个顶点的线性组合，即：
$$
P(t)=k_{0} P_{0}+k_{1} P_{1}+k_{2} P_{2}+\ldots+k_{n} P n
$$
对于 n 阶的贝塞尔曲线，曲线上 t 位置上的点 P(t) 的坐标是由 n+1 个顶点和伯恩斯坦多项式的乘积求和：
$$
P(t)=B_{0}^{n}(t) P_{0}+B_{1}^{n}(t) P_{1}+B_{2}^{n}(t) P_{2}+\ldots+B_{n}^{n}(t) P n=\sum_{i=0}^{n} P_{i} B_{i}^{n}(t)
$$
上面式子也就是Forrest在1972年提出的结论。因此我们就可以使用de Casteljau算法来算曲线上任意一点的坐标，该算法是计算伯恩斯坦多项式的一种递归算法，直接方法相比较慢，但它在数值上更为稳定。

前面我们是从线性插值计算，逆推到伯恩斯坦多项式。现在我们来看看怎么直接使用伯恩斯坦多项式得到递归的结果。

伯恩斯坦多项式具有递归性，即可以把 n 阶的伯恩斯坦多项式写成 n-1 阶的多项式组合：
$$
B_{i}^{n}(t)=(1-t) B_{i}^{n-1}(t)+t B_{i-1}^{n-1}(t)
$$
也就是说原本的方程式：
$$
P(t)=B_{0}^{n}(t) P_{0}+B_{1}^{n}(t) P_{1}+B_{2}^{n}(t) P_{2}+\ldots+B_{n}^{n}(t) P n
$$
可以写成：
$$
\begin{array}{l}P(t)=(1-t) B_{0}^{n-1}(t) P_{0}+\left((1-t) B_{1}^{n-1}(t)+t B_{0}^{n-1}(t)\right) P_{1}+ \ \left((1-t) B_{2}^{n-1}(t)+t B_{1}^{n-1}(t)\right) P_{2}+\ldots+t B_{n-1}^{n-1}(t) P n\end{array}
$$
$ (1-t) B_{0}^{n-1}(t) P_{0}+t B_{0}^{n-1}(t) P_{1} $,提取一下不就变成了 $ B_{0}^{n-1}\left((1-t) P_{0}+t P_{1}\right) $ ，而 $ \left((1-t) P_{0}+t P_{1}\right) $ 就是线性插值。对于后面的几项也是一样的，上面式子就可以写成：
$$
\begin{array}{l}P(t)=\left((1-t) P_{0}+t P_{1}\right) B_{0}^{n-1}(t)+\left((1-t) P_{1}+t P_{2}\right) B_{1}^{n-1}(t)+((1- \left.t) P_{2}+t P_{3}\right) B_{2}^{n-1}(t)+\ldots+\left((1-t) P_{n-1}+t P_{n}\right) B_{n-1}^{n-1}(t)\end{array}
$$
那么就可以把贝塞尔曲线的方程式写成：
$$
\begin{array}{l}P(t)=\sum_{i=0}^{n} P_{i}\left((1-t) B_{i}^{n-1}(t)+t B_{i-1}^{{n-1}(t)\right)=\sum_{i=0}}{n-1}\left((1-t) P_{i}+\right. \left.t P_{i+1}\right) B_{i}^{n-1}(t)\end{array}
$$
也就是说我们把原本 n 个控制点，通过 $ \left((1-t) P_{i}+t P_{i+1}\right) $ 变成了 n-1 个新的控制点。那么 n-1 个控制点又可以按这个方法变成 n-2 个控制点，一直递归下去，最终只剩一个控制点，也就是曲线上的点。这个方法也正是我们之前贝塞尔曲线的绘制过程。