本文最后更新于：2024年5月7日 下午

拟合数学模型时，如果数据中存在少量的异常值，直接拟合会使得模型出现偏差，RANSAC可以有效解决此类问题。

简介

  • 随机抽样一致算法（RANdom SAmple Consensus,RANSAC），采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数，该算法最早由 Fischler 和 Bolles 于1981年提出。

  • 算法通过从数据中随机多次采样，拟合模型，寻找误差最小的模型作为输出结果，根据大数定律，随机性模拟可以近似得到正确结果。

  • RANSAC算法被广泛应用在计算机视觉领域和数学领域，例如直线拟合、平面拟合、计算图像或点云间的变换矩阵、计算基础矩阵等方面。

算法假设

  1. 数据中包含正确数据和异常数据（或称为噪声）。正确数据记为内点（inliers），异常数据记为外点（outliers）。

  2. 对于给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法。

数学原理

  • 假设内点在整个数据集中的概率为t，即：

$$
t=\frac{n_{\text {inliers }}}{n_{\text {inliers }}+n_{\text {outliers }}}
$$

  • 确定该问题的模型需要n个点，这个n是根据问题而定义的，例如拟合直线时n为2，平面拟合时n=3，求解点云之间的刚性变换矩阵时n=3，求解图像之间的射影变换矩阵是n=4，等等。
  • k表示迭代次数，即随机选取n个点计算模型的次数。P为在这些参数下得到正确解的概率。
  • 可以得到，n个点都是内点的概率为 $t^n$，则n个点中至少有一个是外点的概率为

$$
1-t^n
$$

  • $ \left( 1 - t ^ {n} \right) ^ {k} $ 表示k次随机抽样中都没有找到一次全是内点的情况，这个时候得到的是错误解，那么成功的概率为： $$ P=1-\left(1-t^{n}\right)^{k} $$

  • 内点概率t是一个先验值，可以给出一些鲁棒的值。同时也可以看出，即使t给的过于乐观，也可以通过增加迭代次数k，来保证正确解的概率P。

  • 同样的，可以通过上面式子计算出来迭代次数k，即假设需要正确概率为P（例如需要99%的概率取到正确解），则：

$$
k=\frac{\log (1-P)}{\log \left(1-t^{n}\right)}
$$

算法描述

以空间中多个数据点拟合直线为例

  1. 要得到一个直线模型，需要两个点唯一确定一个直线方程。所以第一步随机选择两个点。
  2. 通过这两个点，可以计算出这两个点所表示的模型方程y=ax+b。
  3. 将所有的数据点套到这个模型中计算误差。
  4. 找到所有满足误差阈值的点。
  5. 重复（1）~（4），直到达到一定迭代次数后，选出满足阈值点数量最多的模型作为问题的解。

示例

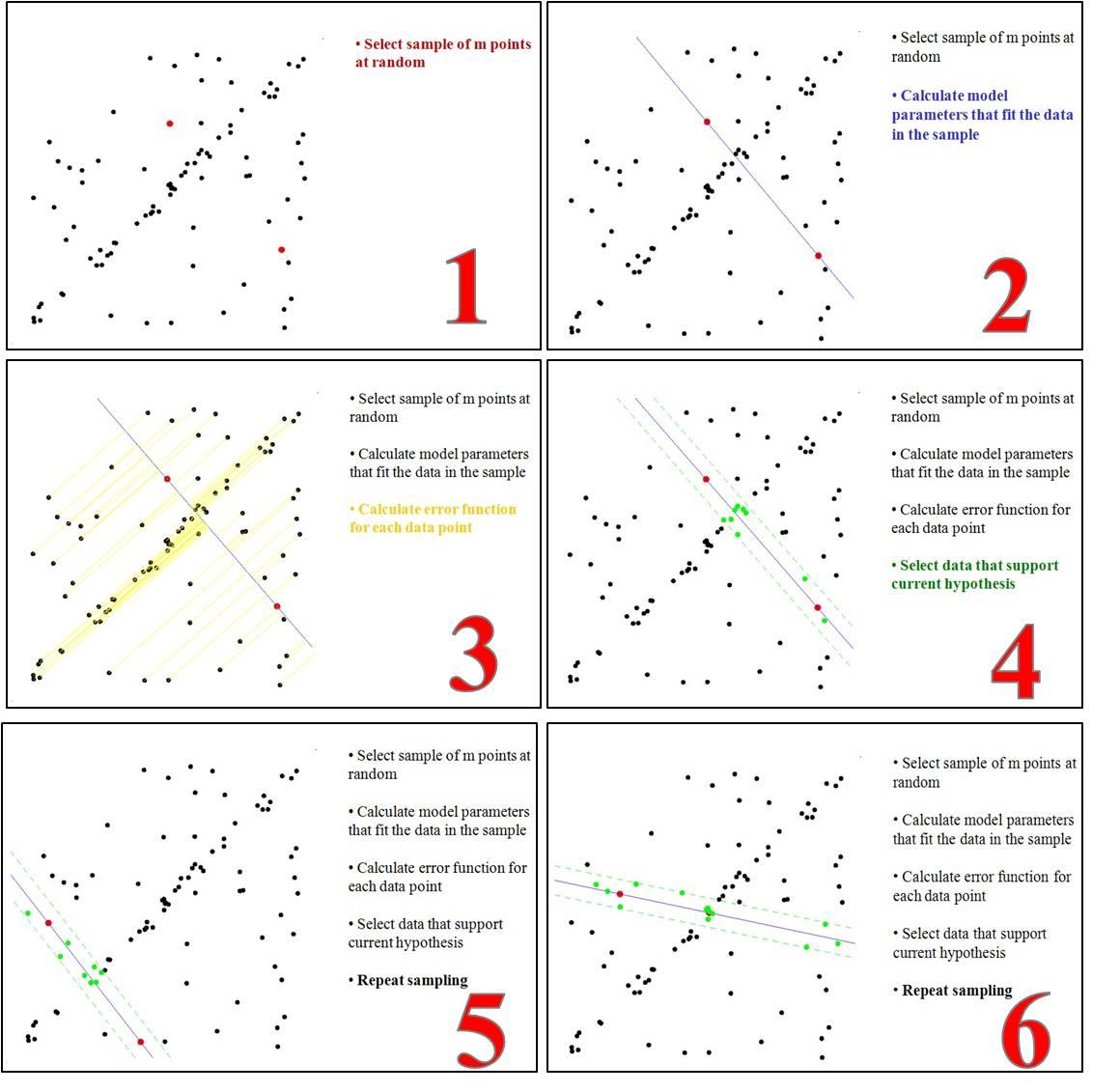
  • 通过多次迭代，可以有很大的概率得到正确拟合的直线

  • 而由于异常数据的干扰，直接用最小二乘拟合很容易带来偏差，这就是 RANSAC 排除异常数据带来的优势

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
from copy import copy
import numpy as np
from numpy.random import default_rng
rng = default_rng()


class RANSAC:
    def __init__(self, n=10, k=100, t=0.05, d=10, model=None, loss=None, metric=None):
        self.n = n              # `n`: Minimum number of data points to estimate parameters
        self.k = k              # `k`: Maximum iterations allowed
        self.t = t              # `t`: Threshold value to determine if points are fit well
        self.d = d              # `d`: Number of close data points required to assert model fits well
        self.model = model      # `model`: class implementing `fit` and `predict`
        self.loss = loss        # `loss`: function of `y_true` and `y_pred` that returns a vector
        self.metric = metric    # `metric`: function of `y_true` and `y_pred` and returns a float
        self.best_fit = None
        self.best_error = np.inf

    def fit(self, X, y):

        for _ in range(self.k):
            ids = rng.permutation(X.shape[0])

            maybe_inliers = ids[: self.n]
            maybe_model = copy(self.model).fit(X[maybe_inliers], y[maybe_inliers])

            thresholded = (
                self.loss(y[ids][self.n :], maybe_model.predict(X[ids][self.n :]))
                < self.t
            )

            inlier_ids = ids[self.n :][np.flatnonzero(thresholded).flatten()]

            if inlier_ids.size > self.d:
                inlier_points = np.hstack([maybe_inliers, inlier_ids])
                better_model = copy(self.model).fit(X[inlier_points], y[inlier_points])

                this_error = self.metric(
                    y[inlier_points], better_model.predict(X[inlier_points])
                )

                if this_error < self.best_error:
                    self.best_error = this_error
                    self.best_fit = maybe_model

        return self

    def predict(self, X):
        return self.best_fit.predict(X)


def square_error_loss(y_true, y_pred):
    return (y_true - y_pred) ** 2

def mean_square_error(y_true, y_pred):
    return np.sum(square_error_loss(y_true, y_pred)) / y_true.shape[0]

class LinearRegressor:
    def __init__(self):
        self.params = None

    def fit(self, X: np.ndarray, y: np.ndarray):
        r, _ = X.shape
        X = np.hstack([np.ones((r, 1)), X])
        self.params = np.linalg.inv(X.T @ X) @ X.T @ y
        return self

    def predict(self, X: np.ndarray):
        r, _ = X.shape
        X = np.hstack([np.ones((r, 1)), X])
        return X @ self.params

if __name__ == "__main__":

    regressor = RANSAC(model=LinearRegressor(), loss=square_error_loss, metric=mean_square_error)

    X = np.array([-0.848,-0.800,-0.704,-0.632,-0.488,-0.472,-0.368,-0.336,-0.280,-0.200,-0.00800,-0.0840,0.0240,0.100,0.124,0.148,0.232,0.236,0.324,0.356,0.368,0.440,0.512,0.548,0.660,0.640,0.712,0.752,0.776,0.880,0.920,0.944,-0.108,-0.168,-0.720,-0.784,-0.224,-0.604,-0.740,-0.0440,0.388,-0.0200,0.752,0.416,-0.0800,-0.348,0.988,0.776,0.680,0.880,-0.816,-0.424,-0.932,0.272,-0.556,-0.568,-0.600,-0.716,-0.796,-0.880,-0.972,-0.916,0.816,0.892,0.956,0.980,0.988,0.992,0.00400]).reshape(-1,1)
    y = np.array([-0.917,-0.833,-0.801,-0.665,-0.605,-0.545,-0.509,-0.433,-0.397,-0.281,-0.205,-0.169,-0.0531,-0.0651,0.0349,0.0829,0.0589,0.175,0.179,0.191,0.259,0.287,0.359,0.395,0.483,0.539,0.543,0.603,0.667,0.679,0.751,0.803,-0.265,-0.341,0.111,-0.113,0.547,0.791,0.551,0.347,0.975,0.943,-0.249,-0.769,-0.625,-0.861,-0.749,-0.945,-0.493,0.163,-0.469,0.0669,0.891,0.623,-0.609,-0.677,-0.721,-0.745,-0.885,-0.897,-0.969,-0.949,0.707,0.783,0.859,0.979,0.811,0.891,-0.137]).reshape(-1,1)

    regressor.fit(X, y)

    import matplotlib.pyplot as plt
    plt.style.use("seaborn-darkgrid")
    fig, ax = plt.subplots(1, 1)
    ax.set_box_aspect(1)

    plt.scatter(X, y)

    line = np.linspace(-1, 1, num=100).reshape(-1, 1)
    plt.plot(line, regressor.predict(line), c="peru")
    plt.show()

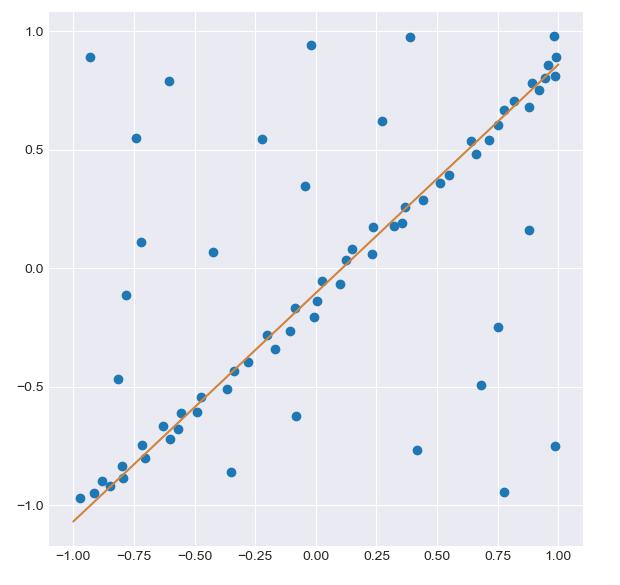
  • 运行结果

    运行 RANSAC 实现的结果。橙线显示了迭代法找到的最小二乘参数，成功地忽略了异常点。

参考资料



文章链接：
https://www.zywvvd.com/notes/study/probability/ransac/ransac/

“觉得不错的话，给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信二维码

微信支付

支付宝二维码

支付宝支付

Probability
#Probability
RANSAC
https://www.zywvvd.com/notes/study/probability/ransac/ransac/
作者
Yiwei Zhang
发布于
2022年8月22日
许可协议