概率论基础 - 13 - 泊松分布（Poisson分布）

本文最后更新于：2024年5月7日下午

本文记录泊松分布。

泊松分布

假设已知事件在单位时间 (或者单位面积) 内发生的平均次数为 $\lambda$, 则泊松分布描述了：事件在单位时间 (或者单位面积) 内发生的具体次数为 $k$ 的概率。
概率质量函数： $ p(X=k | \lambda)=\frac{e^{-\lambda} \lambda^{k}}{k !} $.
期望: $ \mathbb{E}[X]=\lambda $
方差: $ \operatorname{Var}[X]=\lambda$

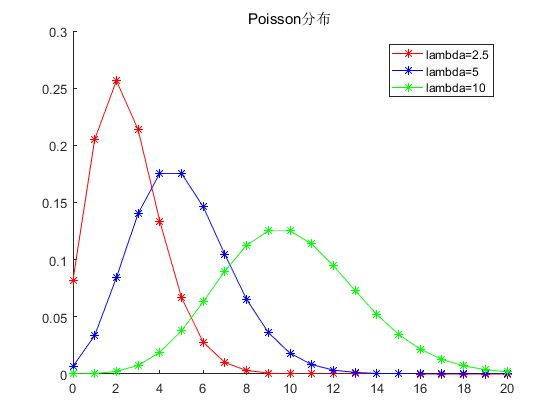
泊松分布的来源

泊松分布单位时间发生的次数为$X$，平均次数为$\lambda$
设所观察的这段时间为[0,1),取一个很大的自然数n，把时间段[0,1)分为等长的n段：

$$
l_{1}=\left[0, \frac{1}{n}\right], l_{2}=\left[\frac{1}{n}, \frac{2}{n}\right], \ldots, l_{i}=\left[\frac{i-1}{n}, \frac{i}{n}\right], \ldots, l_{n}=\left[\frac{n-1}{n}, 1\right]
$$

我们做如下两个假定:

在每段 $ l_{i} $ 内, 恰发生一个事故的概率，近似的与这段时间的长 $ \frac{1}{n} $ 成正比，可设为 $ \frac{\lambda}{n} $ 。当n很大时， $ \frac{1}{n} $ 很小时，在 $ l_{i} $ 这么短暂的一段时间内，要发生两次或者更多次事故是不可能的。因此在 $ l_{i} $ 这段时间内不发生事故的概率为 $ 1-\frac{\lambda}{n} $ 。
$ l_{i}, \ldots, l_{n} $ 各段是否发生事故是独立的
把在 $ [0,1) $ 时段内发生的事故数 X视作在n个划分之后的小时段 $ l_{i}, \ldots, l_{n} $ 内有事故的时段数，则按照上述两个假定， $ X $ 应服从二项分布 $ B\left(n, \frac{\lambda}{n}\right) $ 。于是，我们有

$$ P(X=i)=C_n^i\left(\frac{\lambda}{n}\right)^{i}\left(1-\frac{\lambda}{n}\right)^{n-i} $$

注意到当 $ n \rightarrow \infty $ 取极限时，我们有

$$
\frac{C_n^i}{n{i}} \rightarrow \frac{1}{i !},\left(1-\frac{\lambda}{n}\right)^{n} \rightarrow e^{-\lambda}
$$

因此

$$ \begin{aligned} P(X=i) &=\left(\begin{array}{c} n \\ i \end{array}\right)\left(\frac{\lambda}{n}\right)^{i}\left(1-\frac{\lambda}{n}\right)^{n-i} \\ &=\frac{e^{-\lambda} \lambda^{i}}{i !} \end{aligned} $$

从上述推导可以看出：泊松分布可作为二项分布的极限而得到。一般的说，若 $ X \sim B(n, p) $,其中n很大， p很小，因而 $ n p=\lambda $ 不太大时， X的分布接近于泊松分布 $ P(\lambda) $ 。这个事实有时可将较难计算的二项分布转化为泊松分布去计算。

Python 实现

scipy 包支持模拟泊松分布

查表

查累积概率。查询 $\lambda$ =100，发生次数小于等于120的概率：

from scipy import stats
 
p = stats.poisson.cdf(120, 100)
print(p)

>>>
0.9773306709216473

随机数生成

生成服从 $ambda$ =50的泊松分布随机数100个：

from scipy import stats
# 设置random_state时，每次生成的随机数一样。不设置或为None时，多次生成的随机数不一样
sample = stats.poisson.rvs(mu=50, size=100, random_state=3)
print(sample)

>>>
[51 45 60 40 34 53 54 45 45 49 51 46 48 61 47 53 47 48 45 49 52 45 43 50
 50 54 54 47 47 46 36 72 54 55 52 37 42 41 54 54 55 58 53 53 51 43 58 38
 63 50 44 53 48 43 53 45 67 37 51 42 54 47 59 55 54 55 55 46 60 43 54 45
 59 44 58 45 51 58 56 47 54 33 55 50 58 49 60 37 51 43 50 52 52 45 42 44
 49 54 52 48]