概率论基础 - 16 - Logistic 分布

本文最后更新于：2024年5月7日下午

逻辑回归是机器学习中常用的二分类模型，其理论基础来源于 Logistic 分布，本文介绍相关内容。

定义

Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为：
$$
\begin{array}{c}F(x)=P(X \leq x)=\frac{1}{1+e^{-(x-\mu) / \gamma}} \ f(x)=F^{\prime}(X \leq x)=\frac{e^{-(x-\mu) / \gamma}}{\gamma\left(1+e^{-(x-\mu) / \gamma}\right)^{2}}\end{array}
$$
其中，$\mu$ 为位置参数，$\gamma$ 为形状参数。

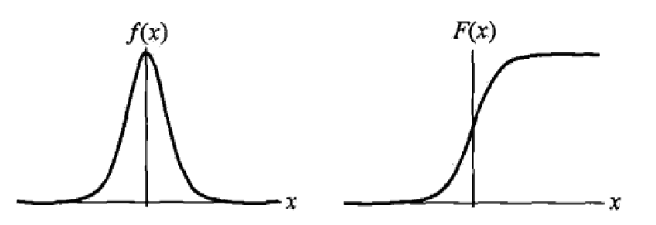
Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在 $ \mu=0, \gamma=1 $ 的特殊形式。

"S"曲线在中心附近增长速度较快，在两端增长速度较慢。形状参数 $\gamma$ 越小，中心附近增长速度越快。(密度函数曲线的胖瘦由 $\gamma$ 决定)。