Logistic Regression

本文最后更新于：2023年12月5日下午

本文介绍逻辑回归算法的原理。

简介

**二项逻辑斯谛回归模型(binomial logistic regression model)**是一种分类模型，并且还是一种二类分类模型。来源于 Logistic 分布。

条件概率分布如下：

$$ \begin{array}{l}P(Y=1 \mid x)=\frac{\exp (\omega \cdot x+b)}{1+\exp (\omega \cdot x+b)} \\ P(Y=0 \mid x)=\frac{1}{1+\exp (\omega \cdot x+b)}\end{array} $$

其中， $ x \in R^{n} $ 是输入， $ Y \in{0,1} $ 是输出， $ \omega \in R^{n} $ 和 $ b \in R $ 是参数， $ \omega $ 称为权值向量，$ \mathrm{b} $ 称为偏置， $ \omega \cdot x $ 为 $ \omega $ 和 $ x $ 的内积。

分类过程

用上面的条件概率分布就能进行分类了，到底是怎么分类的呢？

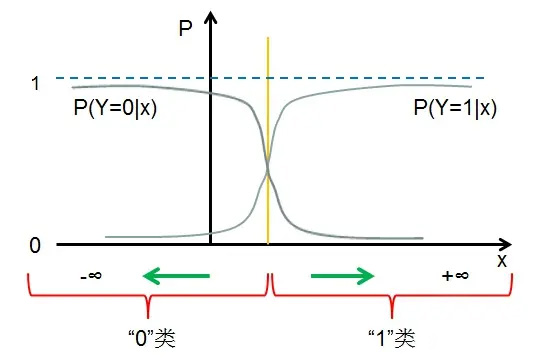
二项逻辑斯谛回归模型的分类原理

仔细看，$P(Y=1|x)$ 的图形(想象一下)很像前面说的逻辑斯谛分布函数的图形，$P(Y=0|x)$ 的图形则刚好和$P(Y=1|x)$ 的图形走势相反。

我们假设 $ x=-\frac{b}{\omega} $ 可知 $P(Y=1|x)与P(Y=0|x)$ 是相等的，都等于 $ 0.5$ ，所以对任意输入 $x$，如果满足 $ x>-\frac{b}{\omega} $ ，即 $P(Y=1|x)>P(Y=0|x)$ 则输出为"1"类，如果满足 $ x<-\frac{b}{\omega} $ ，即 $P(Y=1|x)<P(Y=0|x)$，则输出为"0"类。

即逻辑斯谛回归通过比较两个条件概率值得大小，将实例 $x$ 分到概率值较大的那一类。

本质上就是在和 0.5 作比较。

模型含义

几率

定义：几率是指该事件发生的概率与该事件不发生的概率的比值。即事件发生概率如果是p，那么该事件的几率为 $ \frac{p}{1-p} $。(可以想象，当几率大于1时，说明该事件发生的概率大，几率小于1时，说明该事件发生的概率小)

逻辑回归应用

结合定义，有：
$$
\log \frac{\mathrm{P}(\mathrm{Y}=1 \mid \mathrm{x})}{1-\mathrm{P}(\mathrm{Y}=1 \mid \mathrm{x})}=\omega^T\mathrm{x}
$$
这就是说，在逻辑斯谛回归模型中，输出Y=1的对数几率是输入x的线性函数。或者说，输出 Y = 1 的对数几率是由输入x 的线性函数表示的模型，即逻辑斯谛回归模型。

这就是为什么说**"逻辑斯谛回归模型属于对数线性模型"的原因，因为在逻辑斯谛回归模型中，输出Y=1的对数几率是输入x的线性函数**。

换一个角度看，考虑对输入$x$ 进行分类的线性函数 $\omega^T\mathrm{x}$，其值域为实数域。通过逻辑斯谛回归模型定义式可以将线性函数 $\omega^T\mathrm{x}$ 转换为概率：

$$
\mathrm{P}(\mathrm{Y}=1 \mid \mathrm{x})=\frac{\exp (\mathrm{w} \cdot \mathrm{x})}{1+\exp (\mathrm{w} \cdot \mathrm{x})}
$$

模型参数估计

参数估计就是估计出权值向量 $\omega$ 和偏置值 $b$ 的取值。采用我们熟悉的极大似然估计法来估计模型参数，从而得到逻辑斯谛回归模型。

给定训练数据集 $ T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\} $ 其中， $ x_{i} \in R^{n}, y_{i} \in{0,1} $

设：$ P(Y=1 \mid x)=\pi(x), P(Y=0 \mid x)=1-\pi(x) $

$ \pi(x) $ 是 $ \frac{\exp (\omega \cdot x)}{1+\exp (\omega \cdot x)} $ 的简写

似然函数为：

$$ \prod_{i=1}^{N}\left[\pi\left(x_{i}\right)\right]^{y_{i}}\left[1-\pi\left(x_{i}\right)\right]^{1-y_{i}} $$

取对数得到对数似然函数为：

$$ \begin{array}{l}L(\omega)=\sum_{i=1}^{N}\left[y_{i} \log \pi\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi\left(x_{i}\right)\right)\right]\\= \sum_{i=1}^{N}\left[y_{i} \log \frac{\pi\left(x_{i}\right)}{1-\pi\left(x_{i}\right)}+\log \left(1-\pi\left(x_{i}\right)\right)\right] \\ =\sum_{i=1}^{N}\left[y_{i}\left(\omega \cdot x_{i}\right)-\log \left(1+\exp \left(\omega \cdot x_{i}\right)\right)\right]\end{array} $$

对 $ L(\omega) $ 求极大值，得到 $\omega$ 的估计值。

这样，问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯谛回归学习中通常采用的方法是梯度下降法即拟牛顿法。

其中 $L(\omega)=\sum_{i=1}^{N}\left[y_{i} \log \pi\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi\left(x_{i}\right)\right)\right]$ 的似然函数形式与交叉熵如出一辙。

求解

求解逻辑回归的方法有非常多，我们这里主要聊下梯度下降和牛顿法。优化的主要目标是找到一个方向，参数朝这个方向移动之后使得损失函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是：
$$
J(w)=-\frac{1}{n} ( \sum_{i=1}^{n}\left(y_{i} \ln p\left(x_{i}\right)+\left(1-y_{i}\right) \ln \left(1-p\left(x_{i}\right)\right)\right)
$$

梯度下降

梯度下降是通过 J(w) 对 w 的一阶导数来找下降方向，并且以迭代的方式来更新参数，更新方式为 :

$$ \begin{array}{l}g_{i}=\frac{\partial J(w)}{\partial w_{i}}=\left(p\left(x_{i}\right)-y_{i}\right) x_{i} \\ w_{i}^{k+1}=w_{i}^{k}-\alpha g_{i}\end{array} $$

其中 k 为迭代次数。每次更新参数后，可以通过比较 $ \left\|J\left(w^{k+1}\right)-J\left(w^{k}\right)\right\| $ 小于阈值或者到达最大迭代次数来停止迭代。

牛顿法

牛顿法的基本思路是，在现有极小点估计值的附近对 f(x) 做二阶泰勒展开，进而找到极小点的下一个估计值。假设$ w^{k} $ 为当前的极小值估计值，那么有：

$$ \varphi(w)=J\left(w^{k}\right)+J^{\prime}\left(w^{k}\right)\left(w-w^{k}\right)+\frac{1}{2} J^{\prime \prime}\left(w^{k}\right)\left(w-w^{k}\right)^{2} $$

然后令 $ \varphi^{\prime}(w)=0 $ 得到了 $ w^{k+1}=w^{k}-\frac{J^{\prime}\left(w^{k}\right)}{J^{\prime \prime}\left(w^{k}\right)} $ , 因此有迭代更新式：
$$
w^{k+1}=w{k}-\frac{J^{{\prime}\left(w}{k}\right)}{J^{\prime \prime}\left(w^{{k}\right)}=w}{k}-H_{k}^{-1} \cdot g_{k}
$$
其中 $ H_{k}^{-1} $ 为海森矩阵：

$$ H_{m n}=\frac{\partial^{2} J(w)}{\partial w_{m} \partial w_{n}}=h_{w}\left(x^{(i)}\right)\left(1-p_{w}\left(x^{(i)}\right)\right) x_{m}^{(i)} x_{n}^{(i)} $$

此外，这个方法需要目标函数是二阶连续可微的，本文中的 $J(w) $ 是符合要求的。

多项逻辑斯谛回归

上面介绍的逻辑斯谛回归模型是二项分类模型，用于二类分类。可以将其推广为多项逻辑回归模型（multi-nomial logistic regression model），用于多类分类。假设离散型随机变量Y的取值集合是 ${ 1 , 2 , ⋅ ⋅ ⋅ , K } $，那么多项逻辑斯谛回归模型是:

$$ \begin{array}{c}\mathrm{P}(\mathrm{Y}=\mathrm{k} \mid \mathrm{x})=\frac{\exp \left(\mathrm{w}_{\mathrm{k}} \cdot \mathrm{x}\right)}{1+\sum_{\mathrm{k}=1}^{\mathrm{K}-1} \exp \left(\mathrm{w}_{\mathrm{k}} \cdot \mathrm{x}\right)}, \quad \mathrm{k}=1,2, \cdots, \mathrm{K}-1 \\ \mathrm{P}(\mathrm{Y}=\mathrm{K} \mid \mathrm{x})=\frac{1}{1+\sum_{\mathrm{k}=1}^{\mathrm{K}-1} \exp \left(\mathrm{w}_{\mathrm{k}} \cdot \mathrm{x}\right)}\end{array} $$

其中：$ \mathrm{x} \in \mathbf{R}^{\mathrm{n}+1}, \mathrm{w}_{\mathrm{k}} \in \mathbf{R}^{\mathrm{n}+1} $

二项逻辑斯谛回归的参数估计法也可以推广到多项逻辑斯谛回归。

与其他模型的对比

线性回归

逻辑回归是在线性回归的基础上加了一个 Sigmoid 函数（非线形）映射，使得逻辑回归称为了一个优秀的分类算法。本质上来说，两者都属于广义线性模型，但他们两个要解决的问题不一样，逻辑回归解决的是分类问题，输出的是离散值，线性回归解决的是回归问题，输出的连续值。

我们需要明确 Sigmoid 函数到底起了什么作用：

线性回归是在实数域范围内进行预测，而分类范围则需要在 [0,1]，逻辑回归减少了预测范围；
线性回归在实数域上敏感度一致，而逻辑回归在 0 附近敏感，在远离 0 点位置不敏感，这个的好处就是模型更加关注分类边界，可以增加模型的鲁棒性。

最大熵模型

逻辑回归和最大熵模型本质上没有区别，最大熵在解决二分类问题时就是逻辑回归，在解决多分类问题时就是多项逻辑回归。

SVM

相同点：

都是分类算法，本质上都是在找最佳分类超平面；
都是监督学习算法；
都是判别式模型，判别模型不关心数据是怎么生成的，它只关心数据之间的差别，然后用差别来简单对给定的一个数据进行分类；
都可以增加不同的正则项。

不同点：

LR 是一个统计的方法，SVM 是一个几何的方法；
SVM 的处理方法是只考虑 Support Vectors，也就是和分类最相关的少数点去学习分类器。而逻辑回归通过非线性映射减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重；
损失函数不同：LR 的损失函数是交叉熵，SVM 的损失函数是 HingeLoss，这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。对 HingeLoss 来说，其零区域对应的正是非支持向量的普通样本，从而所有的普通样本都不参与最终超平面的决定，这是支持向量机最大的优势所在，对训练样本数目的依赖大减少，而且提高了训练效率；
LR 是参数模型，SVM 是非参数模型，参数模型的前提是假设数据服从某一分布，该分布由一些参数确定（比如正太分布由均值和方差确定），在此基础上构建的模型称为参数模型；非参数模型对于总体的分布不做任何假设，只是知道总体是一个随机变量，其分布是存在的（分布中也可能存在参数），但是无法知道其分布的形式，更不知道分布的相关参数，只有在给定一些样本的条件下，能够依据非参数统计的方法进行推断。所以 LR 受数据分布影响，尤其是样本不均衡时影响很大，需要先做平衡，而 SVM 不直接依赖于分布；
LR 可以产生概率，SVM 不能；
LR 不依赖样本之间的距离，SVM 是基于距离的；
LR 相对来说模型更简单好理解，特别是大规模线性分类时并行计算比较方便。而 SVM 的理解和优化相对来说复杂一些，SVM 转化为对偶问题后，分类只需要计算与少数几个支持向量的距离，这个在进行复杂核函数计算时优势很明显，能够大大简化模型和计算。

朴素贝叶斯

朴素贝叶斯和逻辑回归都属于分类模型，当朴素贝叶斯的条件概率 $ P\left(X \mid Y=c_{k}\right) $ 服从高斯分布时，它计算出来的 $P(Y=1|X)$ 形式跟逻辑回归是一样的。

两个模型不同的地方在于：

逻辑回归是判别式模型 $p(y|x)$，朴素贝叶斯是生成式模型 $p(x,y)$：判别式模型估计的是条件概率分布，给定观测变量 $x$ 和目标变量 $y$ 的条件模型，由数据直接学习决策函数 $y=f(x)$ 或者条件概率分布 $P(y|x)$ 作为预测的模型。判别方法关心的是对于给定的输入$ x$，应该预测什么样的输出 $y$；而生成式模型估计的是联合概率分布，基本思想是首先建立样本的联合概率概率密度模型 $P(x,y)$，然后再得到后验概率 $P(y|x)$，再利用它进行分类，生成式更关心的是对于给定输入 $x$ 和输出 $y$ 的生成关系；
朴素贝叶斯的前提是条件独立，每个特征权重独立，所以如果数据不符合这个情况，朴素贝叶斯的分类表现就没逻辑回归好了。