概率论基础 - 20 - 二项分布(binomial distribution)

在概率论和统计学中，二项分布（Binomial distribution）是简单但十分重要的基础概率分布，本文介绍相关内容。

简介

在概率论和统计学中，二项分布（英语：Binomial distribution）是 $n$ 个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为 $p$。这样的单次成功/失败试验又称为伯努利试验。实际上，当 $n=1$ 时，二项分布就是伯努利分布。二项分布是显著性差异的二项试验的基础。

概率质量函数

一般来说，若随机变量 $X$ 服从参数为 $n$ 和 $p$ 的二项分布，我们记作 $ =X \sim b(n, p) $ 或 $X \sim B(n, p) $。 $n$ 次试验中正好得到k次成功的概率由概率质量函数给出：

$$ f(k, n, p)=\operatorname{Pr}(X=k)=\left(\begin{array}{l}n \\ k\end{array}\right) p^{k}(1-p)^{n-k} $$

对于 $ k=0,1,2, \cdots, n $ ，其中 $ \left(\begin{array}{l}n \ k\end{array}\right)=\frac{n !}{k !(n-k) !} $

期望

如果 $ X \sim B(n, p) $ , 那么 $X$ 的期望值为
$$
\mathrm{E}[X]=n p
$$

证明

首先假设有一个伯努利试验。试验有两个可能的结果：1 和 0，前者发生的概率为 $p$，后者的概率为 $1-p$ 。该试验的期望值等于 $\mu=1 \cdot p+0 \cdot(1-p)=p $。

一般的二项分布是 $n$ 次独立的伯努利试验的和。它的期望值 :
$$
\mu_{n}=\sum_{k=1}^{n} \mu=n p
$$

方差

如果 $ X \sim B(n, p) $ , 那么 $X$ 的方差为
$$
\operatorname{Var}[X]=n p(1-p)
$$

证明

假设有一个参数为 $p$ 的伯努利试验，方差根据定义计算得到：

$$ \sigma^{2}=(1-p)^{2} \cdot p+(0-p)^{2} \cdot(1-p)=p(1-p) $$

一般的二项分布是 $n$ 次独立的伯努利试验的和。它的方差 :

$$ \sigma_{n}^{2}=\sum_{k=1}^{n} \sigma^{2}=n p(1-p) $$

分布

概率质量函数

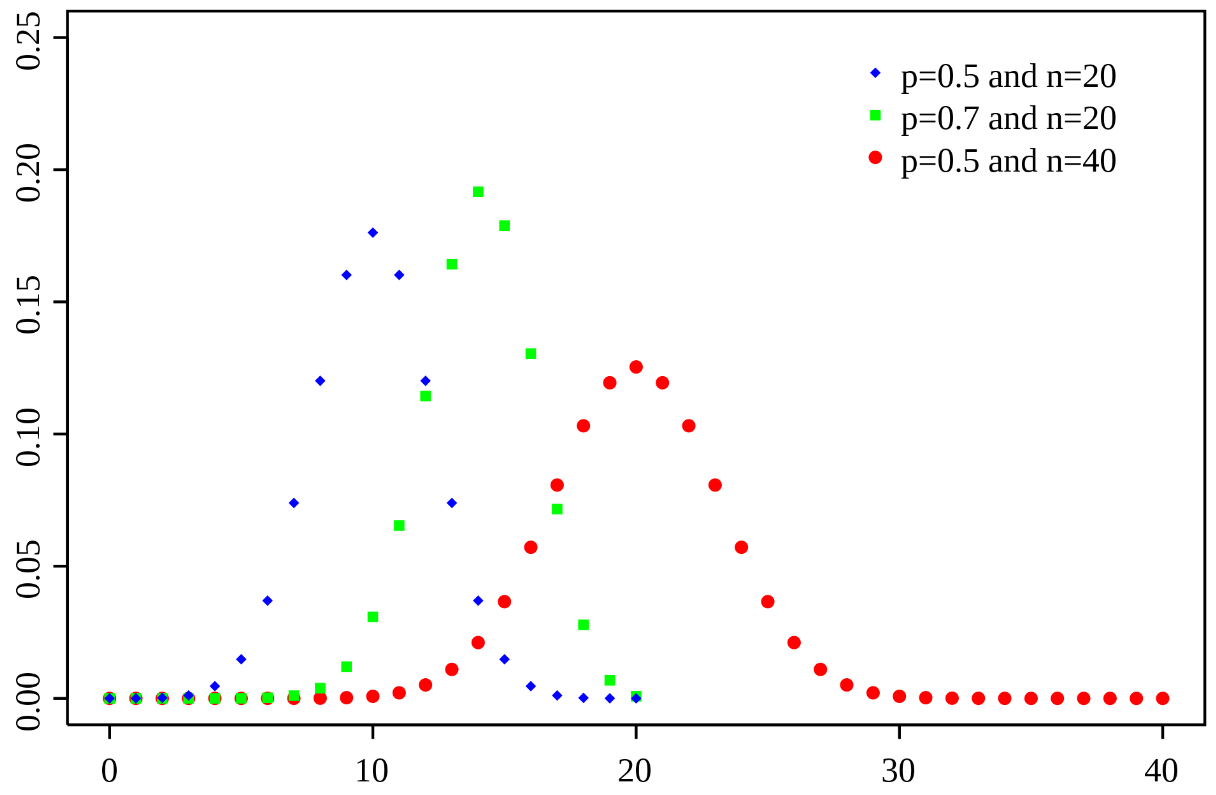
累积分布函数

参考资料

• https://zh.wikipedia.org/zh-cn/二項式分布

文章链接：
https://www.zywvvd.com/notes/study/probability/distributions/binomial-dis/binomial-dis/