本文最后更新于:2024年5月7日 下午
本文记录概率分布常用性质。
分布的性质
概率密度函数
在数学中,连续型随机变量的概率密度函数(Probability density function,简写作PDF ),在不致于混淆时可简称为密度函数,是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。图中,横轴为随机变量的取值,纵轴为概率密度函数的值,而随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分。当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。
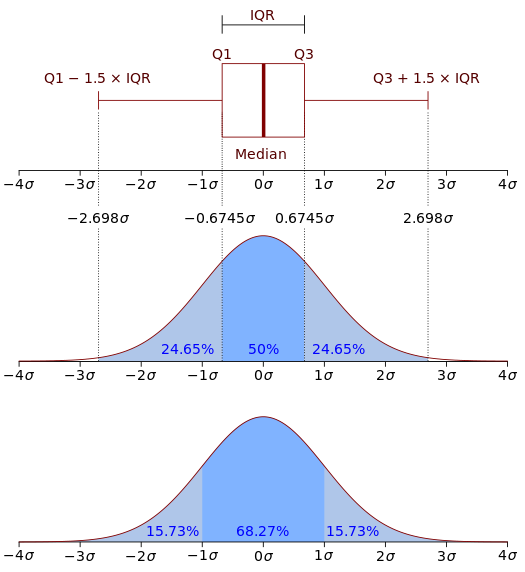
概率密度函数有时也被称为概率分布函数,但这种称法可能会和累积分布函数(CDF)或概率质量函数(PMF)混淆。一般来说,PMF 用于离散随机变量(在可数集上取值的随机变量),而 PDF 用于连续随机变量。
累积分布函数
累积分布函数(英语:cumulative distribution function,CDF)或概率分布函数,简称分布函数,是概率密度函数的积分,能完整描述一个实随机变量X的概率分布。
在标量连续分布的情况下,它给出了从负无穷到 $x$ 的概率密度函数下的面积。 累积分布函数也用于指定多元随机变量的分布。
值域
在数学中,函数的值域(英语:Range)是由定义域中一切元素所能产生的所有函数值的集合。有时候也称为函数的像。
期望
在概率论和统计学中,一个离散性随机变量的期望值(或数学期望,亦简称期望,物理学中称为期待值)是试验中每次可能的结果乘以其结果概率的总和。换句话说,期望值像是随机试验在同样的机会下重复多次,所有那些可能状态平均的结果,便基本上等同“期望值”所期望的数。期望值可能与每一个结果都不相等。换句话说,期望值是该变量输出值的加权平均。期望值并不一定包含于其分布值域,也并不一定等于值域平均值。
方差
方差(英语:variance)又称变异数[1]、变方[2],在概率论及统计学中,描述的是一个随机变量的离散程度,即一组数字与其平均值之间的距离的度量,是随机变量与其总体均值或样本均值的离差的平方的期望值。方差在统计中有非常核心的地位,其应用领域包括描述统计学、推论统计学、假设检验、度量拟合优度,以及蒙特卡洛采样。由于科学分析经常涉及统计,方差也是重要的科研工具。方差是标准差的平方、分布的二阶矩,以及随机变量与其自身的协方差.
中位数
统计学上,中位数(英语:Median),又称中央值、中值,是一个样本、种群或概率分布中之一个数值,其可将数值集合划分为数量相等的上下两部分。对于有限的数集,可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个,则中位数不唯一,通常取最中间的两个数值的平均数作为中位数。
一个数集中最多有一半的数值小于中位数,也最多有一半的数值大于中位数。如果大于和小于中位数的数值个数均少于一半,那么数集中必有若干值等同于中位数。
设连续随机变量X的分布函数为 $F(X)$,那么满足条件 $P(X≤m)=F(m)=1/2$ 的数称为X或分布F的中位数。
对于一组有限个数的数据来说,其中位数是这样的一种数:这群数据的一半的数据比它大,而另外一半数据比它小。
计算有限个数的数据的中位数的方法是:把所有的同类数据按照大小的顺序排列。如果数据的个数是奇数,则中间那个数据就是这群数据的中位数;如果数据的个数是偶数,则中间那2个数据的算术平均值就是这群数据的中位数。
众数
众数(英语:mode)指一组数据中出现次数最多的数据值。例如{8,7,7,8,6,5,5,8,8,8}中,出现最多的是8,因此众数是8,众数可能是一个数(数据值),但也可能是多个数(数据值)。若数据的数据值出现次数相同且无其他数据值时,则不存在众数。例如{5,2,8,2,5,8}中,2、5、8出现次数相同且没有其他数,因此此数据不存在众数。
偏度
偏度(英语:skewness),亦称歪度,在概率论和统计学中衡量实数随机变量概率分布的不对称性。偏度的值可以为正,可以为负或者甚至是无法定义。在数量上,偏度为负(负偏态;左偏)就意味着在概率密度函数左侧的尾部比右侧的长,绝大多数的值(不一定包括中位数在内)位于平均值的右侧。偏度为正(正偏态;右偏)就意味着在概率密度函数右侧的尾部比左侧的长,绝大多数的值(不一定包括中位数)位于平均值的左侧。偏度为零就表示数值相对均匀地分布在平均值的两侧,但不一定意味着其为对称分布。
偏度分为两种:
- 负偏态或左偏态:左侧的尾部更长,分布的主体集中在右侧。
- 正偏态或右偏态:右侧的尾部更长,分布的主体集中在左侧。
如果分布对称,那么平均值=中位数,偏度为零(此外,如果分布为单峰分布,那么平均值=中位数=众数)。
峰度
峰度(英语:Kurtosis),亦称尖度,在统计学中衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。
熵
在信息论中,熵(英语:entropy)是接收的每条消息中包含的信息的平均量,又被称为信息熵、信源熵、平均自信息量。这里,“消息”代表来自分布或数据流中的事件、样本或特征。(熵最好理解为不确定性的量度而不是确定性的量度,因为越随机的信源的熵越大。)来自信源的另一个特征是样本的概率分布。这里的想法是,比较不可能发生的事情,当它发生了,会提供更多的信息。由于一些其他的原因,把信息(熵)定义为概率分布的对数的相反数是有道理的。事件的概率分布和每个事件的信息量构成了一个随机变量,这个随机变量的均值(即期望)就是这个分布产生的信息量的平均值(即熵)。熵的单位通常为比特,但也用Sh、nat、Hart计量,取决于定义用到对数的底。
特征函数
在概率论中,任何随机变量的特征函数(缩写:ch.f,复数形式:ch.f’s)完全定义了它的概率分布。
矩生成函数
在概率论和统计学中,一个实数值随机变量的矩母函数(moment-generating function)又称矩生成函数,矩亦被称作动差,矩生成函数是其概率分布的一种替代规范。 因此,与直接使用概率密度函数或累积分布函数相比,它为分析结果提供了替代途径的基础。 对于由随机变量的加权和定义的分布的矩生成函数,有特别简单的结果。 然而,并非所有随机变量都具有矩生成函数。
顾名思义,矩生成函数可用于计算分布的矩:关于 0 的第 $n$ 个矩是矩生成函数的第 $n$ 阶导数,在 0 处求值。
除了实值分布(单变量分布),矩生成函数可以定义为向量或矩阵值的随机变量,甚至可以扩展到更一般的情况。
与特征函数不同,一个实数值分布的矩生成函数并不总是存在。 分布的矩生成函数的行为与分布的性质之间存在关系,例如矩的存在。
参考资料
文章链接:
https://www.zywvvd.com/notes/study/probability/distribution-nature/distribution-nature/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付