热力学基本定律

本文最后更新于：2024年1月14日晚上

能量可以理解为构成世界的物质，其本身有着基本运行规律，本文记录热力学基本定律。

简介

19世纪，热力学成为一门系统的学科。在19世纪40年代前后，人们已经形成了这样的观念:自然界的各种现象间都是相互联系和转化的。人们对热的研究也不再是孤立地进行，而是在热与其他现象发生转化的过程中认识热，特别是在热与机械功的转比中认识热。
热力学在发展过程中形成了三大基本定律，它们构成了热力学的核心。

热力学第一定律 —— 能量守恒定律

德国物理学家迈尔从1840年起就开始研究自然界各种现象间的转化和联系。在他的论文《与有机运动相联的新陈代谢》中，把热看作“力”(能量)的一一种形式，他指出"热是能够转比为运动的力“。他还根据当时的气体定压和定容比热的资料,计算出热的机械功当量值为367kgm/千k。
在论文中，迈尔详细考察了当时已知的几种自然现象的相互转化，提出了“力“不灭思想，迈尔是最早表述了能量守恒定律也就是热力学第一定律的科学家。

1850年，克劳修斯发表了《论热的动力和能由此推出的关于热学本身的定律》的论文。他认为单一的原理即“在一切由热产生功的情况，有一个和产生功成正比的热量被消耗掉，反之，通过消耗同样数量的功也能产生这样数量的热。” 加上一个原理即“没有任何力的消耗或其它变化的情况下，就把任意多的热量从一个冷体移到热体，这与热素的行为相矛盾”来论证。把热看成是一种状态量。
由此克劳修斯最后得出热力学第一定律的解析式：
$$
dQ=dU-dW
$$

其中 U 表示系统内能，Q 表示系统热量， W 表示外界做功（ W＞0，表示外界对系统做功；W＜0，表示系统对外界做功）
从1854年起，克劳修斯作了大量工作，努力寻找一种为人们容易接受的证明方法来解释这条原理。经过重重努力，1860年，能量守恒原理也就是热力学第一定律开始被人们普遍承认。
定律内容：

能量守恒原理表述为一个系统的总能量的改变只能等于传入或者传出该系统的能量的多少。总能量为系统的机械能、热能及除热能以外的任何内能形式的总和。

第一类永动机

定义：某物质循环一周回复到初始状态，不吸热而向外放热或做功，这叫“第一类永动机”。这种机器不消耗任何能量，却可以源源不断的对外做功。
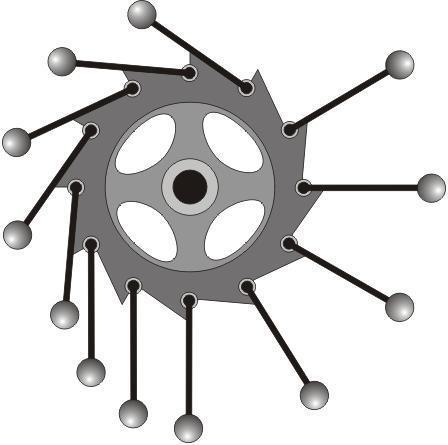
热力学第一定律的出现宣告了第一类永动机的破产，能量守恒，不会凭空产生或消失。

改变能量的方式

热力学第一定律还表述为：一个热力学系统的内能增量ΔU等于外界向它传递的热量Q与外界对它所做的功W的和。
$$
ΔU＝Q＋W
$$
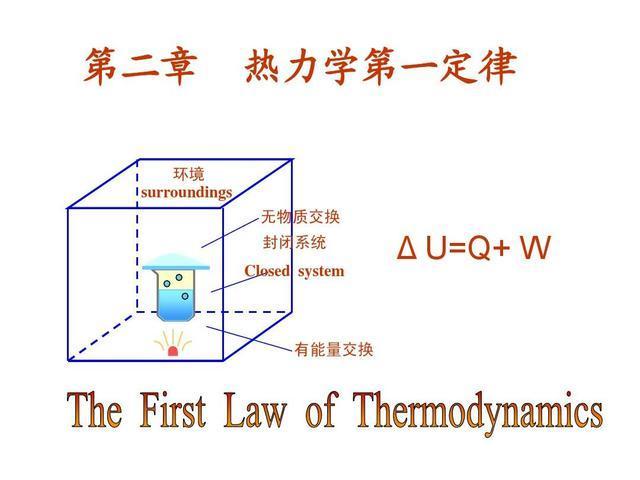
该定律也说明了 做功和热传递是改变物体内能的两种方式。
做功和热传递在改变物体的内能上是等效的。但从能量的转化和守恒的观点来看是有区别的：做功的过程是其他形式的能量和内能之间相互转化的过程，功是能量转化的量度；热传递是内能的转移，热量是内能转移的量度。

昭示了能量转化的可能

热力学第一定律指示了系统内能向做功转化的理论依据，促成了蒸汽机的诞生，直接导致了第一次工业革命
人类由此迈入了蒸汽时代，机械化生产时代开始到来。

热力学第二定律 —— 熵增定律

在热力学发展过程中，牛顿经典力学的一些局限性也暴露了出来，比如牛顿经典力学认为力学过程是可逆的，可逆性是指时间反演，即过程按相反的顺序进行。在经典力学的运动方程中，把时间参量 t换成-t，就意味着过程按相反的顺序历经原来的一切状态，最后回到初始状态。但热力学中的现象不都是可逆的。
1850 年克劳修斯在论文中提出了一条基本定律，也就是热力学第二定律：

没有某种动力的消耗或其他变化，不可能使热从低温转移到高温。

也可以表述为： 在孤立系统内，任何变化不可能导致熵的减少 。

熵此处可以粗浅地理解为系统混乱程度的定量表述，即如果没有外界作用，孤立系统的熵不会自动变少（有序），大多数情况下熵会增加到某种平衡状态。

能量品质

热力学第一定律确定了能量客观存在，且有不同形式，总量守恒。
第二定律核心表述了不同形式能量转化的不可逆性，以机械能和热能为例，可以认为机械能是一种高品质的能量，热能是一种低品质的能量。高品质能量可以很容易地向低品质能量转化，反之则需要额外的代价，表示能量转化的方向性。
热力学第二定律也可以理解为，宇宙的能量守恒，但品质越来越低。
因为热能部分转化成机械能的机器，需要两个温度不同的热源。如果低温热源的温度是$T1$（这里用的都是绝对温标，或称为热力学温标，单位是K，即开尔文），高温热源的温度是$T2$，那么热机的效率（即热能转化成机械能的比例）不可能超过$1 - T1/T2$。在没有摩擦的理想状况下，效率就是这个上限值。

第二类永动机

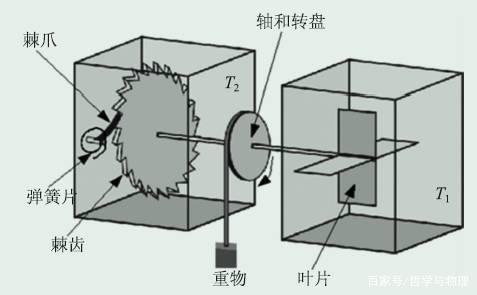
是在热力学第一定律问世后，人们认识到能量是不能被凭空制造出来的，于是有人提出，设计一类装置，从海洋、大气乃至宇宙中吸取热能，并将这些热能作为驱动永动机转动和功输出的源头。
定义： 从单一热源吸热使之完全变为有用功而不产生其它影响的热机称为第二类永动机。
热力学第二定律宣告了第二类永动机理论上的不可能性，问题出在 只有单一的热源，它从这个单一热源吸收的热量，可以全部用来做功，而不引起其他变化。

第二类永动机

熵

克劳修斯从热机的效率出发，认识到正转变（功转变成热量）可以自发进行，而负转变（热量转变成功）作为正转变的逆过程却不能自发进行。负转变的发生需要同时有一个正转变伴随发生，并且正转变的能量要大于负转变，这实际是意味着自然界中的正转变是无法复原的。
后来克劳修斯在 1854 年的随笔《关于热的力学理论的第二基础定理的一个修正形式》提出了新的物理量来解释这种现象,1865 年正式命名为熵, 以符号$S$表示。由此克劳修斯提出了热力学第二定律的又一个表述方式，也被称为熵增原理，那就是：

不可逆热力过程中熵的微增量总是大于零。在自然过程中，一个孤立系统的总混乱度（即“熵”）不会减小。
简而言之就是孤立系统的熵永不自动减少，熵在可逆过程中不变，在不可逆过程中增加，可以说非常鲜明地指出了不可逆过程的进行方向。

熵增原理是热力学第二定律的另外一种表述形式，却又拥有更加深刻的含义，它创造了“熵”这个概念。这个概念在后来被广泛应用，香农把熵的概念，引申到信道通信的过程中，从而开创了”信息论“这门学科，从而宣告了信息时代的到来。

熵增原理表明，在绝热条件下，只可能发生$dS≥0$ 的过程，其中$dS = 0$ 表示可逆过程；$dS>0$表示不可逆过程,$dS<0$ 过程是不可能发生的。但可逆过程毕竟是一个理想过程。因此，在绝热条件下，一切可能发生的实际过程都使系统的熵增大，直到达到平衡态。

热力学第三定律 —— 绝对零度的探索

1702年，法国物理学家阿蒙顿已经提到了“绝对零度”的概念。他从空气受热时体积和压强都随温度的增加而增加设想在某个温度下空气的压力将等于零。根据他的计算，这个温度即后来提出的摄氏温标约为-239°C，后来，兰伯特更精确地重复了阿蒙顿实验，计算出这个温度为-270.3°C。他说，在这个“绝对的冷”的情况下，空气将紧密地挤在一起。现代物理测定绝对零度温度为 -273.15°C。
1906年，德国物理学家能斯特在研究低温条件下物质的变化时，把热力学的原理应用到低温现象和化学反应过程中，发现了一个新的规律，这个规律被表述为：“当绝对温度趋于零时，凝聚系(固体和液体）的熵（即热量除以温度的商）在等温过程中的改变趋于零。”
德国著名物理学家普朗克把这一定律改述为：“当绝对温度趋于零时，固体和液体的熵也趋于零。”这就消除了熵常数取值的任意性。1912年，能斯特又将这一规律表述为绝对零度不可能达到原理，也就是热力学第三定律：

不可能使一个物体冷却到绝对温度的零度。
根据普朗克的表述，可以认为温度为绝对零度的系统熵值为0，降低系统熵需要外界系统做功，而系统本身的熵与系统粒子运动程度相关，系统粒子运动程度可以看做是外界通过做功减少系统熵值的转化率，熵值趋于零的同时，系统趋于绝对零度，基本上可说差不多没有粒子运动的能量，转化率也同时趋于零，系统更难受到外界做功减少熵，而且永远到不了 0 值。现代科学可以使用绝热去磁的方法达到$5×10^{ -10}K$，但永远达不到$0K$。

热力学第零定律 —— 系统热平衡

热力学第零定律表述为：

如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡(温度相同)，则它们彼此也必定处于热平衡。
第零定律是在不考虑引力场作用的情况下得出的，物质（特别是气体物质）在引力场中会自发产生一定的温度梯度。如果有封闭两个容器分别装有氢气和氧气，由于它们的分子量不同，它们在引力场中的温度梯度也不相同。如果最低处它们之间可交换热量，温度达到相同，但由于两种气体温度梯度不同，则在高处温度就不相同，也即不平衡。因此第零定律不适用引力场存在的情形。
第零定律比起其他任何定律更为基本，但直到二十世纪三十年代前一直都未有察觉到有需要把这种现象以定律的形式表达。第零定律是由英国物理学家拉尔夫·福勒于1939年正式提出，比热力学第一定律和热力学第二定律晚了80余年，但是第零定律是后面几个定律的基础，所以叫做热力学第零定律。