SuperPixel 超像素分割 SLIC 算法

本文最后更新于：2024年1月14日晚上

超像素是把一张图片中具有相似特征的像素进行聚类，形成一个更具有代表性的大“像素”。本文记录相关内容。

简介

(a) 原图 (b) 人眼分割 (c) 超像素分割 (d) 基于c的分割

超像素由一系列位置相邻且颜色、亮度、纹理等特征相似的像素点组成的小区域。这些小区域大多保留了进一步进行图像分割的有效信息，且一般不会破坏图像中物体的边界信息，用少量的超像素代替大量像素表达图像特征，降低了图像处理的复杂度，一般作为分割算法的预处理步骤。
超像素分割可以用于跟踪，标签分类，超像素词袋，视频前景分割，骨架提取，人体姿态估计，医学图像分割等对分割的速度有要求的应用。
超像素是把一张图片中具有相似特征的像素进行聚类，形成一个更具有代表性的大“像素”。这个新的像素可以作为其他图像处理算法的基本单位，可以减低图像的维度和异常像素点。目前常用的超像素分割算法有SLIC、SEEDS和LSC。
超像素算法的优秀属性：
- 超像素应当良好地粘附到图像边界。
- 当作为预处理步骤用于降低的计算复杂度时，超像素应当快速计算，存储器效率高且易于使用。
- 当用于分割目的时，超像素应当增加速度并提高结果的质量。

SLIC

线性迭代聚类（SLIC）超像素算法，它采用k均值聚类方法高效地生成超像素。尽管它很简单，但SLIC较以前的算法可以更好地获取边界，同时，它具有更快的速度，更高的内存效率，并且能提高分割性能，也可以直接扩展到超体元生成。
SLIC利用了简单的聚类（贪婪）算法，初始时，每一个聚类的中心被平均的分布在图像中，而超像素的个数，可以基本由这些中心点来决定。每一步迭代，种子像素合并周围的像素，形成超像素。

使用SLIC分割成尺寸（大约）为64,256和1024的超豫素

算法

初始化

默认情况下，算法的唯一参数是k，其含义是大小大致相等的超像素的个数。
对于CIELAB色彩空间中的彩色图像，聚类过程从初始化步骤开始，其中k个初始聚类中心为：
$$
C_{i}=\left[l_{i}, a_{i}, b_{i}, x_{i}, y_{i},\right]^{T}
$$
在间隔S个像素的规则网格上采样。为了产生大致相等大小的超像素，网格间隔为
$$
S=\sqrt{\frac{N}{k}}
$$

其中 N 为像素个数，可以理解为每个超像素面积为 $N/k$，S 为边长

将中心移动到与3×3邻域中的最低梯度位置相对应的种子位置。这样做是为了避免将超像素定位在边缘上，并且减少用噪声像素接种超像素的机会。

分配

定义每个聚类中心周围$2S×2S$ 范围为该中心的搜索范围，即该中心会与搜索范围内的所有像素度量距离，确定关联关系
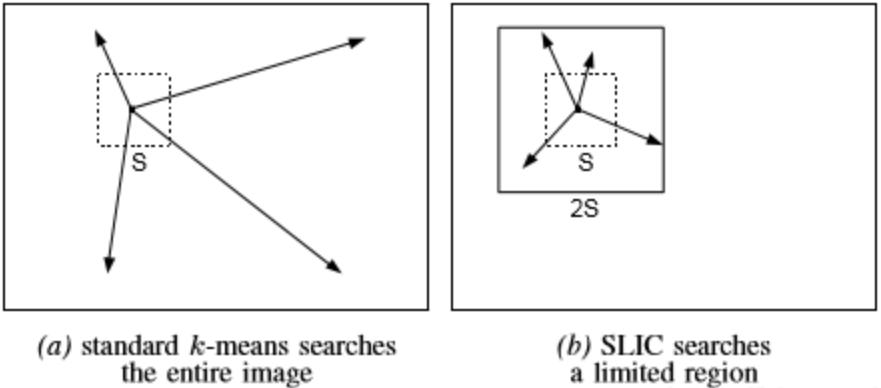
- 该范围限制了每个中心的计算区域，大大加速了 Kmeans 算法的运算速度
- 这种方法不仅减少了距离计算，而且使得SLIC的复杂性与超像素的数量无关
每个像素 $i$ 与搜索区域包含该位置的所有聚类中心度量距离（下文描述），将该像素与距离最小的聚类中心相关联
所有像素都找到了关联的中心后，计算L2 范数的 Loss，之后就可以进行下一次迭代了
直到误差收敛或完成迭代次数

距离度量

SLIC 距离度量分为两部分，颜色差异和欧式距离差异，两组差异需要归一化后计算最终距离度量
颜色距离和欧式距离定义为：
$$ \begin{align} d_{c}&=\sqrt{\left(l_{j}-l_{i}\right)^{2}+\left(a_{j}-a_{i}\right)^{2}+\left(b_{j}-b_{i}\right)^{2}} \\ d_{s}&=\sqrt{\left(x_{j}-x_{i}\right)^{2}+\left(y_{j}-y_{i}\right)^{2}} \end{align} $$
用它们在簇内的各自的最大距离 $ N_{s} $ 和 $ N_{c} $来标准化颜色接和空间的接近程度，用 $D’$ 表示：
$$ D^{\prime}=\sqrt{\left(\frac{d_{c}}{N_{c}}\right)^{2}+\left(\frac{d_{s}}{N_{s}}\right)^{2}} $$
给定群集内预期的最大空间距离对应于采样间隔：
$$
N_{s}=S=\sqrt{\frac{N}{K}}
$$
确定最大的颜色距离 $N_c$ 不是那么简单。因为颜色距离可以从簇到簇和图像到图像显著不同。这个问题可以通过将$N_c$固定为常数 $m$来避免 :

$$ D^{\prime}=\sqrt{\left(\frac{d_{c}}{m}\right)^{2}+\left(\frac{d_{s}}{S}\right)^{2}} $$

变形后得到 $D$ 即为我们在实践中使用的距离测量：
$$ D=\sqrt{d_{c}^{2}+\left(\frac{d_{s}}{S}\right)^{2} m^{2}} $$

总结流程

Python 示例

官方文档：https://docs.opencv.org/3.4/df/d6c/group__ximgproc__superpixel.html

语法：

1	`retval = cv2.ximgproc.createSuperpixelSLIC(image[, algorithm[, region_size[, ruler]]] )`

其中各个参数意义如下：

参数	含义
image	输入图像
algorithm	选择要使用的算法变体：SLIC、SLICO（默认）和MSLIC三种可选
region_size	平均超像素大小，默认10
ruler	超像素平滑度，默认10

示例代码

import cv2

img = cv2.imread("./cat.png")

#初始化slic项，超像素平均尺寸20（默认为10），平滑因子20
slic = cv2.ximgproc.createSuperpixelSLIC(img,region_size=20,ruler = 20.0)
slic.iterate(10)                                    #迭代次数，越大效果越好
mask_slic = slic.getLabelContourMask()              #获取Mask，超像素边缘Mask==1
label_slic = slic.getLabels()                       #获取超像素标签
number_slic = slic.getNumberOfSuperpixels()         #获取超像素数目
mask_inv_slic = cv2.bitwise_not(mask_slic)
img_slic = cv2.bitwise_and(img,img,mask =  mask_inv_slic)  #在原图上绘制超像素边界
cv2.imshow("img_slic",img_slic)
cv2.waitKey(0)
cv2.destroyAllWindows()