本文最后更新于:2024年5月7日 下午
信息熵是一种信息不确定性的度量,而两个随机变量分布匹配程度的度量可以使用KL散度。
定义
KL 散度(Kullback–Leibler divergence,简称KLD),也称作相对熵(relative entropy),信息散度(information divergence),信息增益(information gain)。
- KL散度是两个概率分布$P$和$Q$差别的非对称性的度量。
- KL散度是用来度量使用基于$Q$的编码来编码来自P的样本平均所需的额外的比特个数。 典型情况下,$P$表示数据的真实分布,$Q$表示数据的理论分布,模型分布,或$P$的近似分布。
- 根据 shannon 的信息论,给定一个字符集的概率分布,我们可以设计一种编码,使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X,对$x∈X$,其出现概率为$P(x)$,那么其最优编码平均需要的比特数等于这个字符集的熵:
$$
H\left( X \right) = - \sum\nolimits_{x \in X} {P\left( x \right)logP\left( x \right)}
$$
字符$x$出现的概率为$P(x)$,那么编码$x$需要的最优长度为$log(P(x))$,$H(X)$即为编码字符集$X$的期望编码长度,即按照概率加权平均,也不失为信息熵的一种理解方法。
应用场景
在同样的字符集上,假设存在另一个概率分布$Q(X)$。如果用概率分布$P(X)$的最优编码(即字符$x$的编码长度等于$log[1/P(x)]$,来为符合分布$Q(X)$的字符编码,那么表示这些字符就会比理想情况多用一些比特数。KL散度就是用来衡量这种情况下平均每个字符多用的比特数,因此可以用来衡量两个分布的距离。即:
$$ \begin{array}{l} D_{KL}({Q||P}) &= {\sum _{x \in X}}Q\left( x \right){\rm{log}}\frac{1}{{P(x)}}{\rm{ }} - {\rm{ }}{\sum _{x \in X}}Q\left( x \right){\rm{log}}\frac{1}{{Q(x)}}\\ &= {\sum _{x \in X}}Q\left( x \right)log\left[ {Q\left( x \right)/P\left( x \right)} \right] \end{array} $$$D_{KL}({Q||P})$的意思就是用$P$的最优编码方法($\rm{log}\frac{1}{{P(X)}}$)来编码$Q$分布中的变量,这种编码需要付出的额外编码长度
性质
$ \mathrm{KL} $ 散度非负
- 当它为 0 时, 当且仅当 $ \mathrm{P} $ 和 $ \mathrm{Q} $ 是同一个分布 $ ( $ 对于离散型随机变量), 或者两个分布几乎 处处相等 (对于连续型随机变量) 。
证明:
$$ \begin{array}{l} {D_{KL}}\left( {Q||P} \right){\rm{ }} &= {\rm{ }} - {\sum _{x \in X}}Q\left( x \right)log\left[ {P\left( x \right)/Q\left( x \right)} \right]{\rm{ }} \\ &= {\rm{ }}E\left[ { - logP\left( x \right)/Q\left( x \right)} \right] \end{array} $$由于$-log(x)$是凸函数,因此有:
$$ E\left[ { - logP\left( x \right)/Q\left( x \right)} \right]{\rm{ }} \ge - logE\left[ {P\left( x \right)/Q\left( x \right)} \right] $$ $$ - logE\left[ {P\left( x \right)/Q\left( x \right)} \right] = {\rm{ - }}log{\sum _{x \in X}}Q\left( x \right)P\left( x \right)/Q\left( x \right){\rm{ }} = {\rm{ }}0 $$当$P(x)=Q(x)$时等式成立
$ \mathrm{KL} $ 散度不对称
$$
D_{K L}(P | Q) \neq D_{K L}(Q | P)
$$
直观上看对于 $ D_{K L}(P | Q) $, 当 $ P(x) $ 较大的地方, $ Q(x) $ 也应该较大,这样才能使得 $ P(x) \log \frac{P(x)}{Q(x)} $ 较 小。
对于 $ P(x) $ 较小的地方, $ Q(x) $ 就没有什么限制就能够使得 $ P(x) \log \frac{P(x)}{Q(x)} $ 较小。这就是 $ \mathrm{KL} $ 散度不满足对 称性的原因。
示例
假设真实分布 $ P $ 为混合高斯分布,它由两个高斯分布的分量组成。如果希望用普通的高斯分布 $ Q $ 来近 似 $ P $, 则有两种方案:
$$ \begin{aligned} Q_{1}^{*} &=\arg \min _{Q} D_{K L}(P \| Q) \\ Q_{2}^{*} &=\arg \min _{Q} D_{K L}(Q \| P) \end{aligned} $$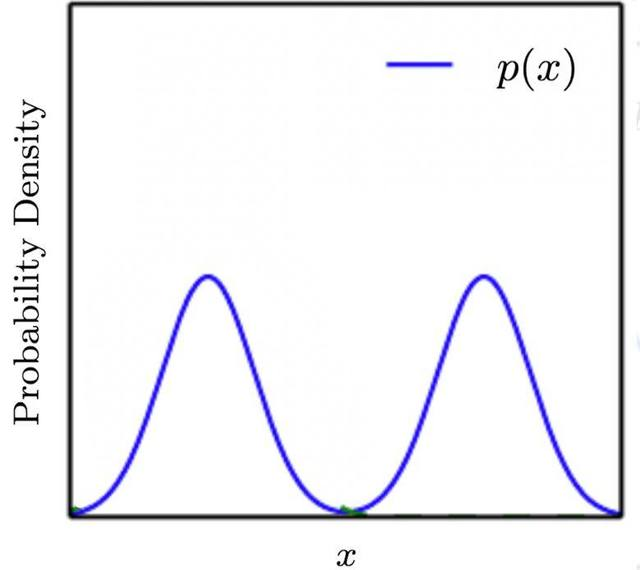
如果选择 $ Q_{1}^{*} $, 则:
-
当 $ P(x) $ 较大的时候 $ Q(x) $ 也必须较大。如果 $ P(x) $ 较大时 $ Q(x) $ 较小, 则 $ P(x) \log \frac{P(x)}{Q(x)} $ 较大。
-
当 $ P(x) $ 较小的时候 $ Q(x) $ 可以较大,也可以较小
因此 $ Q_{1} ^ { * } $ 会贴近 $ P(x) $ 的峰值。由于 $ P(x) $ 的峰值有两个, 因此 $ Q_{1} ^ { * } $ 无法偏向任意一个峰值,最终结果就是 $ Q_{1}^{*} $ 的峰值在 $ P(x) $ 的两个峰值之间。

如果选择 $ Q_{2}^{*} $, 则:
-
当 $ P(x) $ 较小的时候, $ Q(x) $ 必须较小。如果 $ P(x) $ 较小的时 $ Q(x) $ 较大,则 $ Q(x) \log \frac{Q(x)}{P(x)} $ 较大
-
当 $ P(x) $ 较大的时候, $ Q(x) $ 可以较大,也可以较小。
- 因此 $ Q_{2}^{*} $ 会贴近 $ P(x) $ 的谷值。最终结果就是 $ Q_{2}^{*} $ 会贴合 $ P(x) $ 峰值的任何一个。
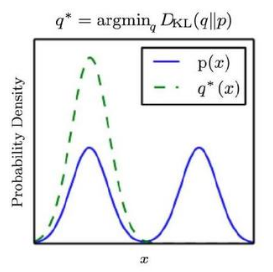
绝大多数场合使用 $ D_{K L}(P | Q) $
原因是:当用分布 $ Q $ 拟合 $ P $ 时我们希望对于常见的事件, 二者概率相 差不大。
参考资料
文章链接:
https://www.zywvvd.com/notes/study/information-theory/cross-entropy-KL-divergence/KL-divergence/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付