本文最后更新于:2024年5月7日 下午
孤立森林是一种超脱的异常检测算法,本文记录原理和实现。
简介
孤立森林(isolation Forest)算法,2008年由刘飞、周志华等提出,算法不借助类似距离、密度等指标去描述样本与其他样本的差异,而是直接去刻画所谓的疏离程度(isolation),因此该算法简单、高效,在工业界应用较多。
Isolation Forest算法的逻辑很直观,算法采用二叉树对数据进行分裂,样本选取、特征选取、分裂点选取都采用随机化的方式。
基本假设是异常点的特征距离正常数据比较远,而且数量不多。
基于这一假设,如果有个人随机生成特征空间中的平面来切分所有数据点的话,那么异常的点应该会以更大的概率被很快单独分割到某个子空间去。这也就是孤立森林的核心思想了。
形象说明

给你根棍子,还把你眼睛蒙上,要把上图的白棋扒拉出来,找个人在边上给你计数,看多少次能分出来,A这一堆,需要的次数非常多,可能一早上你都扒拉不出来;而B这一堆,可能一次就扒拉出来了,需要的次数非常少,那我们就可以通过计算扒拉的次数来衡量一个点的异常程度了,扒拉的次数越少,越不合群,也就越异常。一个人扒拉可能存在随机性,不大准,那我们找100个人来扒拉,然后将每个人扒拉的次数取的平均,那不就准了,孤立森林,大概也就是这个思想了。
论文示例
论文中给了图示,在一堆二维数据中,考虑孤立点 $x_0$ 和正常点 $x_i$
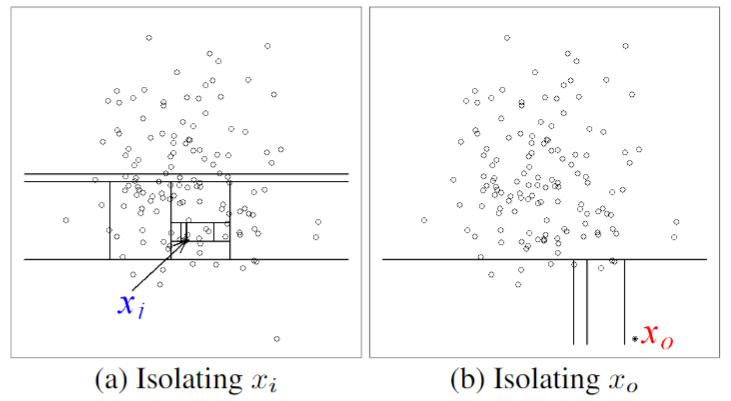
在二维空间中随机划分,将二者分到独立子空间中,多次组织划分,记录每次达到目的的次数,绘制统计图:

可以看到 $x_0$ 需要的划分次数要明显少很多,依此判断 $x_0$ 更为异常。
数据说明
假设现在有一组一维数据(如下图),我们要对这组数据进行切分,目的是把点A和 B单独切分出来,先在最大,值和最小值之间随机选择一个值 X,然后按照 <X 和 >=X 可以把数据分成左右两组,在这两组数据中分别重复这个步骤,直到数据不可再分。
点B跟其他数据比较疏离,可能用很少的次数就可以把它切分出来,点 A 跟其他数据点聚在一起,可能需要更多的次数才能把它切分出来。
那么从统计意义上来说,相对聚集的点需要分割的次数较多,比较孤立的点需要的分割次数少,孤立森林就是利用分割的次数来度量一个点是聚集的(正常)还是孤立的(异常)。
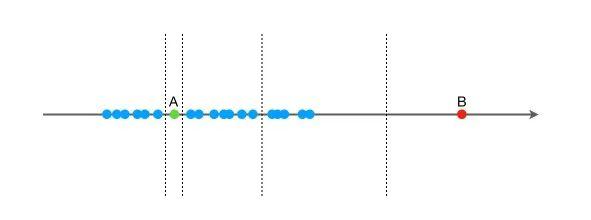
直观上来看,我们可以发现,那些密度很高的簇要被切很多次才会停止切割,即每个点都单独存在于一个子空间内,但那些分布稀疏的点,大都很早就停到一个子空间内了。
注: 所谓单独切分是指在现有的空间分割方案中的一个子空间内随机切分,切分的结果子空间中,如果只包含一个元素,那么我们称该元素被单独切分了出来,之后这个空间不会再次进行切分。
原理
孤立森林算法具体实现时,需要为样本数据维护一棵棵决策树,每个决策就是在切分特征空间,直到达到了切分次数极限或者所有样本都单独待在一个子空间之内。
随机选择m个特征,通过在所选特征的最大值和最小值之间随机选择一个值来分割数据点。观察值的划分递归地重复,直到所有的观察值被孤立(或达到最大分割次数)。
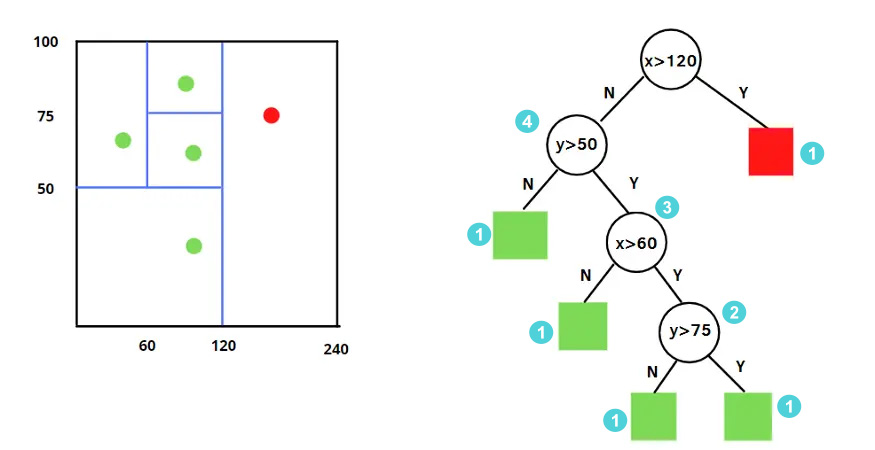
此时每个数据点记录自己所在决策树的层数,我们倾向于相信层数越低的数据越异常,但是一棵树不足以说明问题,于是同样的方法多生成一些树:

训练
1)训练逻辑
从原始数据中,有放回或者不放回的抽取部分样本,选取部分特征,构建一颗二叉树(iTree即Isolation Tree),利用集成学习的思想,多次抽取样本和特征,完成多棵iTree的构建。
2)iTree停止条件
树达到指定的高度/深度,或者数据不可再分。
3)算法伪代码如下


完成训练或,我们获得了 $t$ 棵完成训练的决策树。
- 树的最大深度=ceiling(log(subsimpleSize)),paper里说自动指定,sklearn也是在代码中写死:max_depth = int(np.ceil(np.log2(max(max_samples, 2))))这个值接近树的平均深度,我们只关注那些小于平均深度的异常值,所以无需让树完全生长
- Sub-sampling size,每次抽取的样本数,建议256即可,大于256,性能上不会有大的提升
- Number of tree,建议100,如果特征和样本规模比较大,可以适当增加
预测
树已经有了,接下来需要评价数据样本的异常程度,按照之前描述的思想, 很容易想到用该样本落入叶子结点时,split的次数(即样本落入叶子结点经过的边)作为衡量指标,对于 $t$ 棵树,取平均即可。
对于比较异常的样本,一般没有到达切分最大次数就到达叶子节点了,对于落入树中叶子节点位置的样本,直接统计其树的高度即可;但是当样本众多,叶子节点不是一个样本(经常发生)时,就没有直观的拆分次数用于评估了。
PathLength计算
此时如果直接用该节点的高度其实可能会出问题,因为既然该节点里有不止一个样本,那么肯定达到了最大拆分次数,如果直接使用高度,可能会导致大量的样本在此处评价异常程度时具有相同的权重,很可能导致本该有所区分的样本没有分开;那节点里不止一个样本该怎么办呢,既然统一太粗鲁,我们就尝试细分节点直接的区别,考虑叶子节点的情况,我们倾向于认为比较异常的样本落在的叶子节点里的节点数应该会比很正常的样本落在的叶子节点里的样本数少(这句话有点绕,但是道理就是这样的),那么就需要将这部分差异表现出来。
最暴力的差异表现手段当然是接着划分子空间啦,直到将所有数据分开,但是运算量巨大(不然为啥设置拆分数量上限),那么在不往下拆分的情况下还得估计节点所在数的高度,就需要做估计了。
$$
h(x)=e+c( T.size )
$$
其中e为样本 $x$ 从树的根节点到叶节点的过程中经历的边的个数,即 split 次数。$T.size$ 表示和样本 $x$ 同在一个叶子结点样本的个数,$C(T.size)$ 可以理解为在此处建立一棵节点数为 $T.size$ 的树中节点的平均高度,表示 $T.size$个样本构建一个二叉树的平均路径长度,也就是说这里的节点为了节约时间就不算了,但是每个节点咱们估计一个高度大家拿去用就行了,$c(n)$ 计算公式如下:
其中,0.5772156649为欧拉常数
计算异常分
样本落入叶子结点经过的边数(split次数),除了和样本本身有关,也和 limit length 和抽样的样本子集有关系。这里,作者采用归一化的方式,把 split length 的值域映射到 0-1 之间。具体公式如下:
$$
s(x, n)=2^{-\frac{E(h(x))}{c(n)}}
$$
其 中:
h(x): 为样本在iTree上的PathLength
E(h(x)): 为样本在t棵iTree的PathLength的均值
c(n): 为n个样本构建一个BST二叉树的平均路径长度,为什么要算这个,因为iTree和BST的结构的等价性, 标准化借鉴BST(Binary Search Tree)去估计路径的平均长度c(n)。
上述公式,指数部分值域为(−∞,0),因此s值域为(0,1)。当PathLength越小,s越接近1,此时样本为异常值的概率越大。
当观测的得分接近1时,路径长度非常小,那么数据点很容易被孤立,我们有一个异常。当观测值小于0.5时,路径长度就会变大,然后我们就得到了一个正常的数据点。如果所有的观察结果都有0.5左右的异常值,那么整个样本就没有任何异常。
实现
异常检测的工具还是很多的,主要有以下几个,我们这次选用的是Scikit-Learn进行实验。
- PyOD: 超过30种算法,从经典模型到深度学习模型一应俱全,和sklearn的用法一致
- Scikit-Learn: 包含了4种常见的算法,简单易用
- TODS: 与PyOD类似,包含多种时间序列上的异常检测算法
1 | |
参数详解
n_estimators : int, optional (default=100)
iTree的个数,指定该森林中生成的随机树数量,默认为100个
max_samples : int or float, optional (default=”auto”)
构建子树的样本数,整数为个数,小数为占全集的比例,用来训练随机数的样本数量,即子采样的大小
如果设置的是一个int常数,那么就会从总样本X拉取max_samples个样本来生成一棵树iTree
如果设置的是一个float浮点数,那么就会从总样本X拉取max_samples * X.shape[0]个样本,X.shape[0]表示总样本个数
如果设置的是"auto",则max_samples=min(256, n_samples),n_samples即总样本的数量
如果max_samples值比提供的总样本数量还大的话,所有的样本都会用来构造数,意思就是没有采样了,构造的n_estimators棵iTree使用的样本都是一样的,即所有的样本
contamination : float in (0., 0.5), optional (default=0.1)
取值范围为(0., 0.5),表示异常数据占给定的数据集的比例,数据集中污染的数量,其实就是训练数据中异常数据的数量,比如数据集异常数据的比例。定义该参数值的作用是在决策函数中定义阈值。如果设置为’auto’,则决策函数的阈值就和论文中定义的一样
max_features : int or float, optional (default=1.0)
构建每个子树的特征数,整数位个数,小数为占全特征的比例,指定从总样本X中抽取来训练每棵树iTree的属性的数量,默认只使用一个属性
如果设置为int整数,则抽取max_features个属性
如果是float浮点数,则抽取max_features * X.shape[1]个属性
bootstrap : boolean, optional (default=False)
采样是有放回还是无放回,如果为True,则各个树可放回地对训练数据进行采样。如果为False,则执行不放回的采样。
n_jobs : int or None, optional (default=None)在运行fit()和predict()函数时并行运行的作业数量。除了在joblib.parallel_backend上下文的情况下,None表示为1。设置为-1则表示使用所有可用的处理器
random_state : int, RandomState instance or None, optional (default=None)
每次训练的随机性
如果设置为int常数,则该random_state参数值是用于随机数生成器的种子
如果设置为RandomState实例,则该random_state就是一个随机数生成器
如果设置为None,该随机数生成器就是使用在np.random中的RandomState实例
verbose : int, optional (default=0)
训练中打印日志的详细程度,数值越大越详细
warm_start : bool, optional (default=False)当设置为True时,重用上一次调用的结果去fit,添加更多的树到上一次的森林1集合中;否则就fit一整个新的森林
方法
fit(X[, y, sample_weight]):训练模型
decision_function(X):返回平均异常分数
predict(X):预测模型返回1或者-1
fit_predict(X[, y]):训练-预测模型一起完成
get_params([deep]):Get parameters for this estimator.
score_samples(X):Opposite of the anomaly score defined in the original paper.
set_params(**params):Set the parameters of this estimator.
1 | |
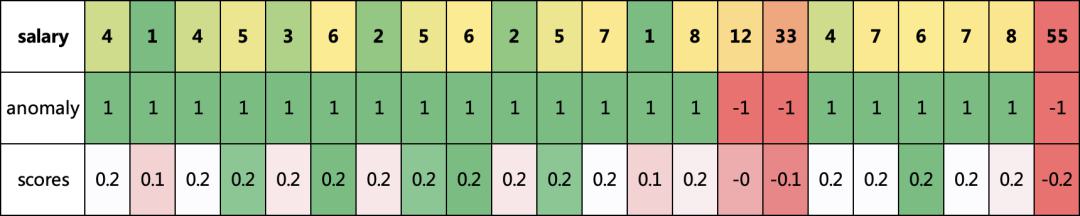
我们可以看到,发现了三个异常的数据,和我们认知差不多,都是比较高的,并且异常值越大,异常分scores就越大
原始论文
参考资料
- https://zhuanlan.zhihu.com/p/492469453
- https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf
- https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.IsolationForest.html#sklearn.ensemble.IsolationForest
文章链接:
https://www.zywvvd.com/notes/study/machine-learning/isolation-forest/isolation-forest/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付