旋转矩阵

本文最后更新于：2024年1月14日晚上

矩阵乘法可以理解为空间的映射，本文记录旋转矩阵的作用。

矩阵乘法

矩阵乘法可以理解为向量之间的投影，左侧矩阵的行向量与右侧矩阵的列向量投影作为结果。

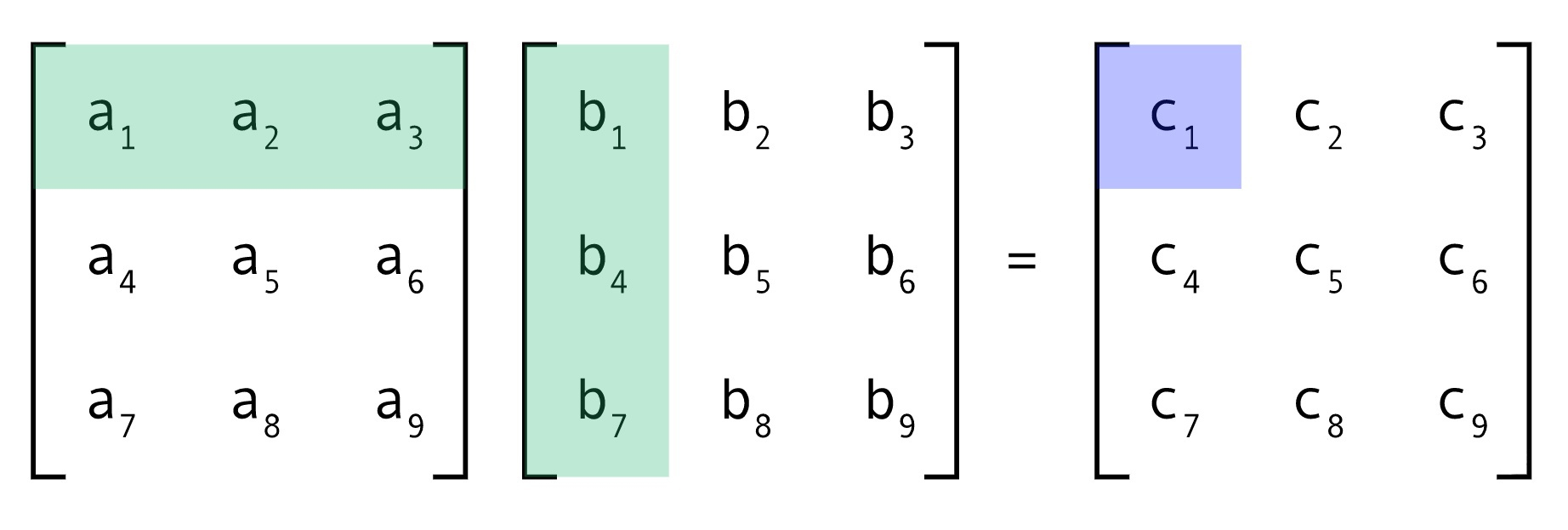
当左侧矩阵为 $N$ 维空间上的一组基时，这种乘法又可以看做是在求解原始空间中的向量 $[b_1,b_4,b_7]$ 在空间中新的基下的表示 $[c_1,c_4,c_7]$ 。

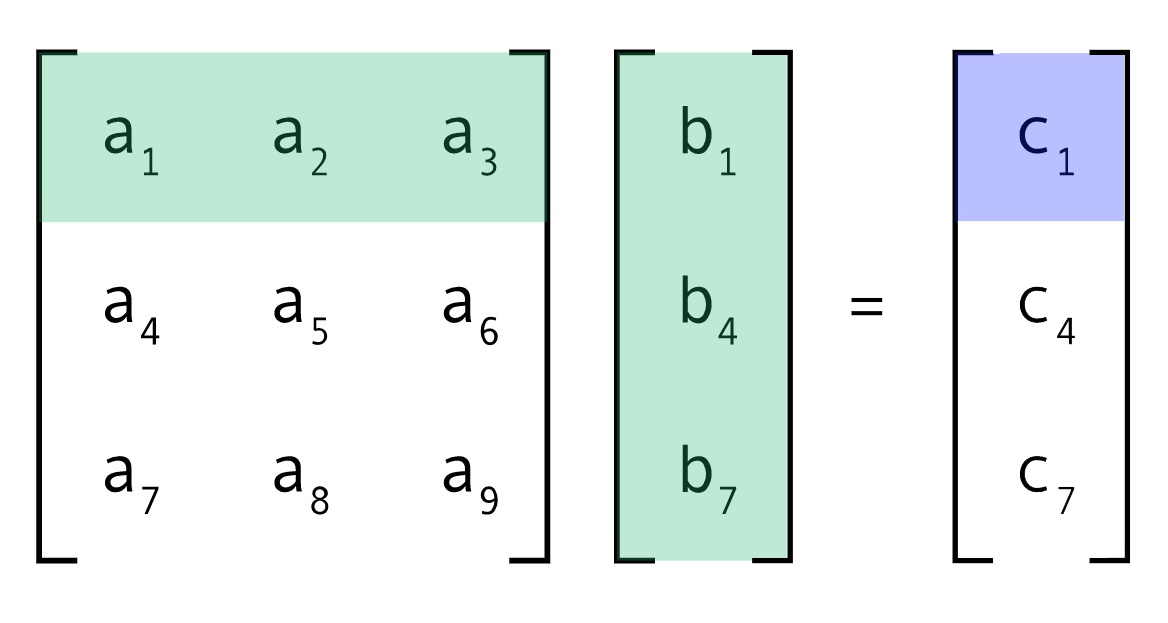
如果基的模长为1，那么求解原始空间中向量在新空间表示的长度时，其实就是原始向量在各个单位向量基上的投影长度，这也是基一般都是单位长度的原因。

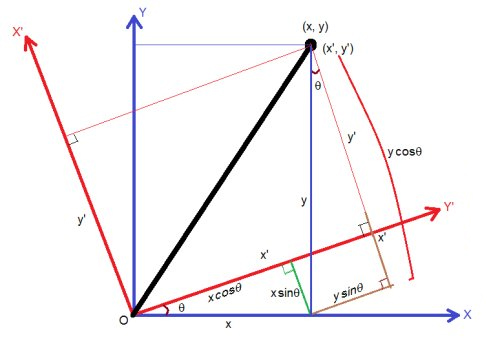
旋转矩阵是特殊的单位基，用角度和三角函数表示基的大小，例如 $[\cos \theta,\sin\theta]$

这样基天然就是单位长度，而且带有可解释的含义，经过这样的基映射后，相当于原始空间的某个轴旋转了某个角度 $\theta$

旋转示例

原始二维笛卡尔坐标系空间中的一点 $A(x,y)$，现将 $X$ 轴和 $Y$ 轴分别逆时针旋转 $\theta _ x$ , $\theta _ y$ 角度，之后原始的 $A$ 点在新空间有新的表示 $A’(x’,y’)$。

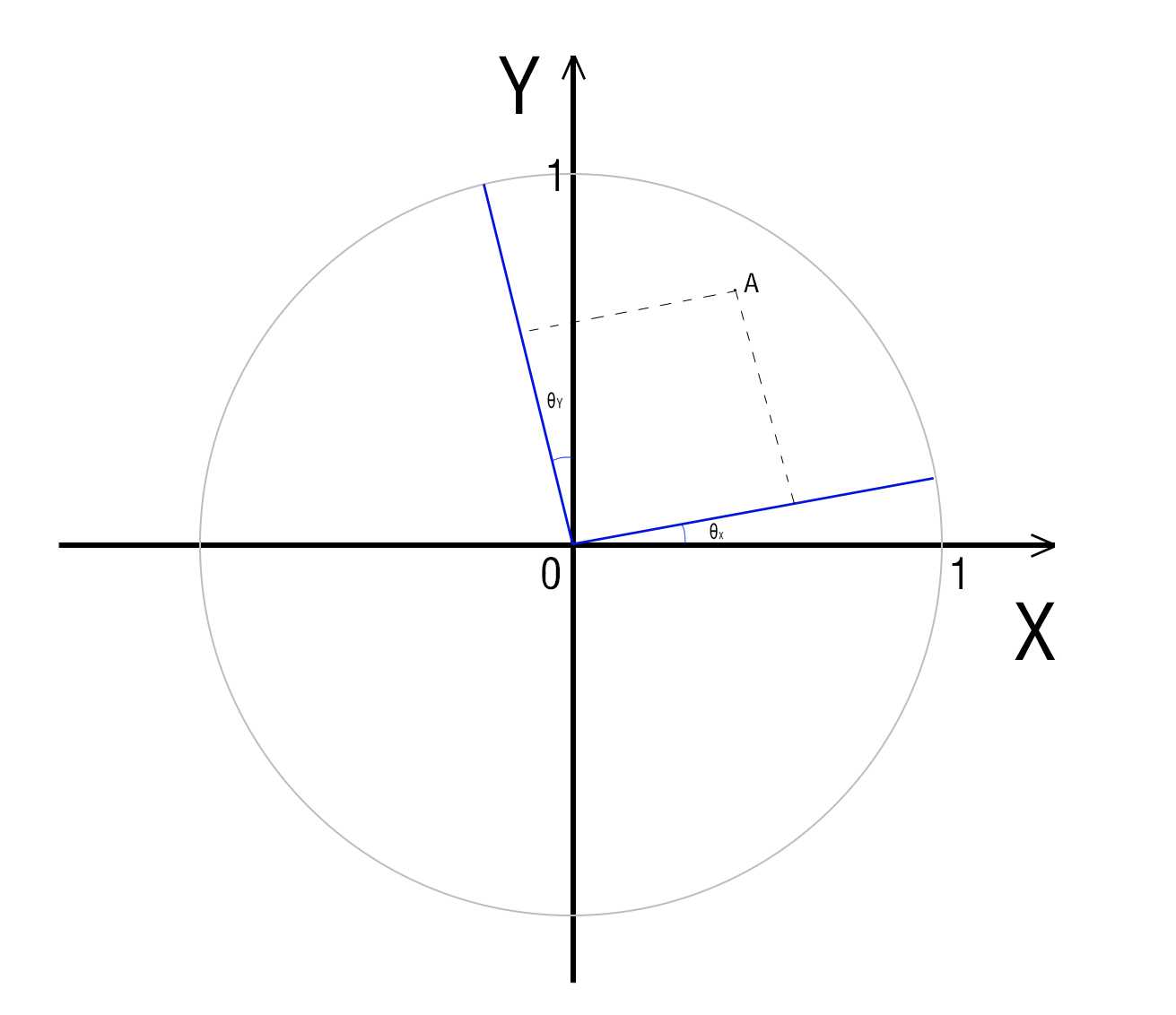
新的 $X$ 轴在原始坐标系下的单位向量为 $[\cos \theta_x,\sin \theta_x]$，新的 $Y$ 轴在原始坐标系下的单位向量为 $[-\sin \theta_y,\cos \theta_y]$

那么 $A$ 在新坐标系下的坐标为 $OA$ 向量分别到两个单位向量的投影长度：

$$ \begin{array}{l} x'=x\cos \theta_x+y\sin\theta_x\\ y'=-x\sin \theta_y+y\cos\theta_y\\ \end{array} $$

这也就完成了 $A$ 的坐标系转换，用矩阵表示就是：

$$ RA= \left[\begin{array}{cc}\cos \theta_x & \sin \theta_x \\ -\sin \theta_y & \cos \theta_y\end{array}\right] \left[\begin{array}{cc}x \\ y \end{array}\right] = \left[\begin{array}{cc}x' \\ y' \end{array}\right] $$

其中 $R =\left[\begin{array}{cc}\cos \theta_x & \sin \theta_x \\ -\sin \theta_y & \cos \theta_y\end{array}\right] $ 也就是旋转矩阵，这里表示的是 $X,Y$ 轴不一定垂直的特殊旋转，一般常用的旋转矩阵为 $\theta_x = \theta_y$，这里的是更一般的应用场景。