线性变换(linear transformation)

线性变换 (linear transformation) 是在生活和项目中经常见到的映射方式， 是线性代数(linear algebra)的基本概念，它是一类满足某些特殊性质的变换，本文介绍相关内容。

没人能够清楚地告诉你矩阵是什么，你必须自己亲自看看。 —— 墨菲斯

简介

国外很多线性代数课程的第一课便是线性变换，这个概念比矩阵来的更早。物理学家们通常更关注这个概念本身，关注它们是怎么变换的。但是在我们的学习中为了更方便的计算，引入了坐标系及坐标轴，并且使每一个线性变换都对应一个矩阵，矩阵背后也同样是线性变换的概念。

相关定义

变换

变换从本质上讲就是函数的意思。函数的意思就是把一个集合中元素对应到另外一个集合中元素的对应法则。

在线性代数里面，由所有 $n$ 维向量组成一个集合，这些向量之间可以进行加减法运算和数乘运算。把可以进行这两种运算的集合通常成为一个线性空间(linear space)，它其中的一组基(basis)所包含的向量的个数，称为线性空间的维度(dimension)。可以看出，所有 $n$ 维向量组成的集合就是一个 $n$ 维线性空间，通常记为$R^n$。

所以总结为一句话：变换的本质，就是从一个线性空间到另一个线性空间的函数。

线性变换

几何要素

线性变换从几何直观有三个要点：

1. 变换前是直线的，变换后依然是直线
2. 直线比例保特不变
3. 变换前是原点的，变换后依然是原点

定义描述

线性映射（ linear mapping）是从一个向量空间 $V$ 到另一个向量空间 $W$ 的映射且保持加法运算和数量乘法运算，而线性变换（linear transformation）是线性空间 $V$ 到其自身的线性映射。 —— 百度百科

公式表示

你可以将线性变换理解为一个特殊的函数，这个可以使得 $ V \rightarrow W $ ，并且满足以下条件:

$$ \begin{array}{l}\mathbf{T}(\mathbf{x}+\mathbf{y})=\mathbf{T}(\mathbf{x})+\mathbf{T}(\mathbf{y}) \\ \mathbf{T}(a \mathbf{x})=a \mathbf{T}(\mathbf{x})\end{array} $$

其中 $ x, y \in V ， a \in R $ 。

性质

1. 两个線性映射的复合映射是線性的: 如果 $ f: V \rightarrow W $ 和 $ g: W \rightarrow Z $ 是線性的，則 $ g \circ f: V \rightarrow Z $ 也是線性的。

2. 若線性映射可逆，則该線性映射的逆也是線性映射。

3. 如果 $ f_{1}: V \rightarrow W $ 和 $ f_{2}: V \rightarrow W $ 是線性的，則它们的和 $ f_{1}+f_{2} $ 也是線性的(这是由 $ \left(f_{1}+f_{2}\right)(x)=f_{1}(x)+f_{2}(x) $ 定义的)。

4. 如果 $ f: V \rightarrow W $ 是線性的，而 $ a $ 是基础域 $ K $ 的一个元素，則定义自 $ (a f)(x)=a(f(x)) $ 的映射 $ a f $ 扡是線性的。

5. 给定有限维的情况，如果基已经选择好了，則線性映射的复合对应于矩阵乘法，線性映射的加法对应于矩阵加法，而線性映射与标量的乘法对应于矩阵与标量的乘法。

示例

线性变换

$$
\mathbf{f}(x, y, z)=(3 x-y, 3 z, 0, z-2 x)
$$

非线性变换

$$ \begin{array}{c}\mathbf{g}(x, y, z)=(3 x-y, 3 z+2,0, z-2 x) \\ \mathbf{h}(x, y, z)=(3 x-y, 3 x z, 0, z-2 x)\end{array} $$

这两个都不是线性变换。

1. 在函数 $ g $ 中，第二个分量为 $ 3 z+2 ， 2 $ 是一个常数，并不包含输 入向量 $ (x, y, z) $ 中的任何分量，也可以换种解释方法，按照 $(1)$ 中的第二个公式，应有 $T(0)=0$，而$g(0,0,0)=(0,2,0,0) $ 与上式矛盾。
2. 在函数 $h$ 中，很明显含有一个非线性分量 $ 3 x z $ ，因此也不是一个线性变换。

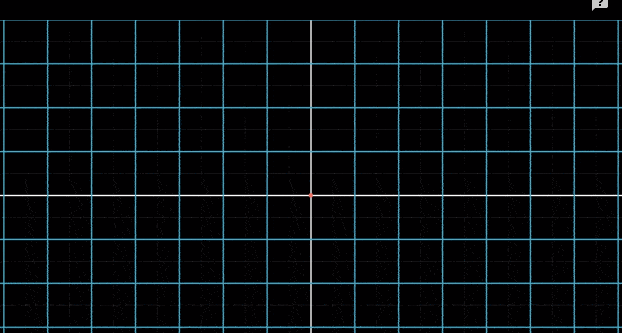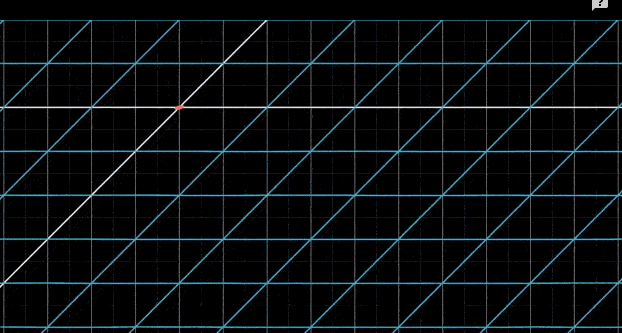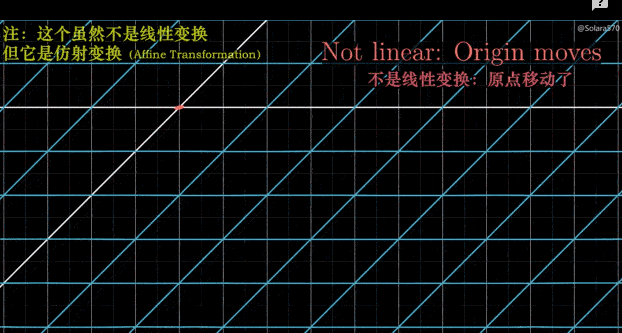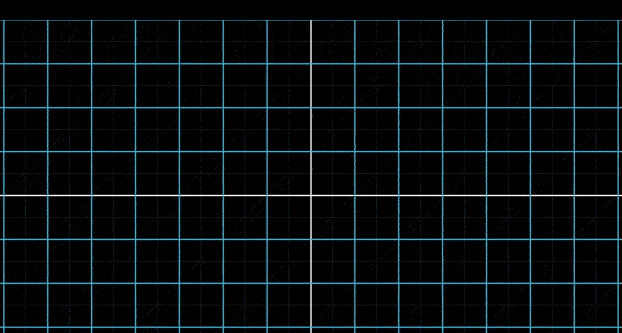
非线性变换图示

1. 变换后不能保持直线

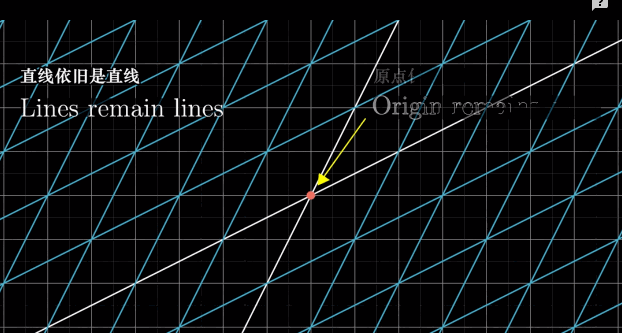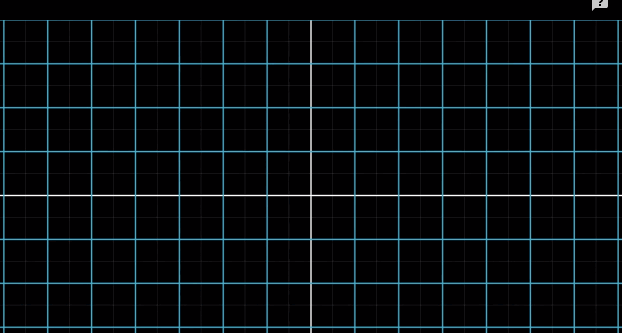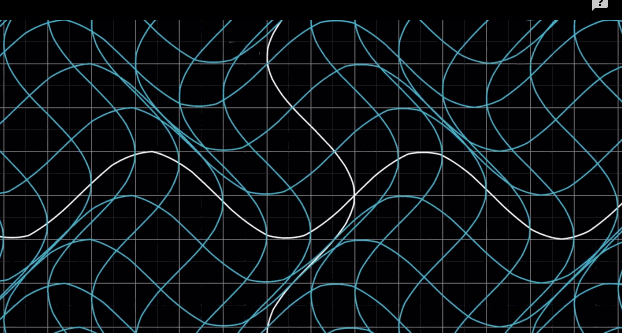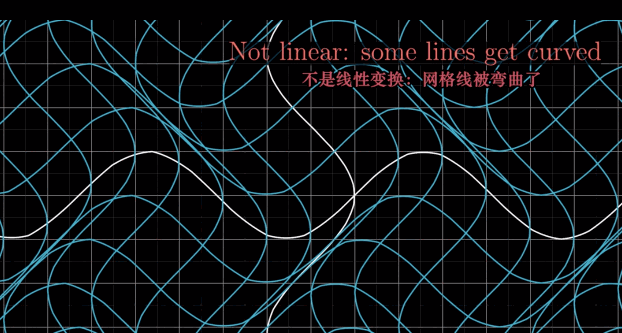
2. 变换后原点位置发生了变化 如：在二维平面上的仿射变换（在 3 维视角下仍然时线性变换）

矩阵表示

如果 $ V $ 和 $ W $ 是有限维的，并且在这些空间中有选择好的基，則从 $ V $ 到 $ W $ 的所有线性映射可以被表示为矩阵。反过来说，矩阵生成线性映射的例子：如果 $ A $ 是实 数的 $ m \times n $ 矩阵，则规定 $ f(x)=A x $ 描述一个线性映射 $ R^{n} \rightarrow R^{m} $ 。

设 $ \left\{v_{1}, \cdots, v_{n}\right\} $ 是 $ V $ 的一个基。則在 $ V $ 中所有向量 $ v $ 是唯一的，可以由

$$
c_{1} v_{1}+\cdots+c_{n} v_{n}
$$
的系数 $ c_{1}, \cdots, c_{n} $ 确定。

如果 $ f: V \rightarrow W $ 是线性映射
$$
f\left(c_{1} v_{1}+\cdots+c_{n} v_{n}\right)=c_{1} f\left(v_{1}\right)+\cdots+c_{n} f\left(v_{n}\right)
$$
这蕴涵了这个函数 $ f $ 是完全由

$$
f\left(v_{1}\right), \cdots, f\left(v_{n}\right)
$$
的值确定的。

现在设 $ \left\{w_{1}, \ldots, w_{m}\right\} $ 是 $ W $ 的基。則可以表示每个 $ f\left(v_{j}\right) $ 的值为
$$
f\left(v_{j}\right)=a_{1 j} w_{1}+\cdots+a_{m j} w_{m}
$$
因此函数 $ f $ 是完全由 $ a_{i, j} $ 的值确定的。

如果把这些值放置到 $ m \times n $ 矩阵 $ M $ 中，則可以方便的使用它来计算 $ f $ 对在 $ V $ 中任何向量的值。如果我放置 $ c_{1}, \cdots, c_{n} $ 的值到 $ n \times 1 $ 矩阵 $ C $ ，我们有 $ M C=f(v) $。

一个单一的线性映射可以由很多矩阵表示。这是因为矩阵的元素的值依赖于选择的基。

矩阵表示的优点

对角化的矩阵具有诸多优点。线性映射在写成矩阵后可以进行对角化（不能对角化的矩阵可以化简成接近对角矩阵的准对角矩阵，从而可以获得对角化矩阵拥有的独特优势（极大地简化乘法运算，易于分块，容易看出与基的选取无关的不变量。

比如，对于作用于同一个空间的可对角化的方形矩阵 $ A $ ，要求出 $ A $ 自乘 $ n $ 次后的结果 $ A^{n} $ ，一个一个慢慢地乘是很麻烦的事情。而知道对角化技巧的人会发现，在将这矩阵对角化后，其乘法运算会变得格外简单。实际应用中有很多有意思的问题或解题方法都会涉及到矩阵自乘n次的计算，如1阶非齐次线性递推数列通项公式的线性代数求解法和马尔可夫链的极限状态（极限分布）的求解。线性代数及矩阵论的一个主要问题就是寻找可使矩阵对角化的条件或者可使矩阵化简到含很多个 0 的条件，以便简化计算（这是主要原因之一）。

线性变换矩阵例子

二维空间 $ R^{2} $ 的線性變換的一些特殊情况有:

• 逆时针旋转90度：

$$ A=\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right] $$

• 逆時針旋轉 $\theta$ 度:

$$ A=\left[\begin{array}{cc}\cos (\theta) & -\sin (\theta) \\ \sin (\theta) & \cos (\theta)\end{array}\right] $$

• 针对 y 轴反射：

$$ A=\left[\begin{array}{cc}1 & 0 \\ 0 & -1\end{array}\right] $$

• 在所有方向上放大2倍：

$$ A=\left[\begin{array}{ll}2 & 0 \\ 0 & 2\end{array}\right] $$

• 水平错切：

$$ A=\left[\begin{array}{cc}1 & m \\ 0 & 1\end{array}\right] $$

• 挤压：

$$ A=\left[\begin{array}{cc}k & 0 \\ 0 & 1 / k\end{array}\right] $$

• 向 y 轴投影：

$$ A=\left[\begin{array}{ll}0 & 0 \\ 0 & 1\end{array}\right] $$

仿射变换的线性性

上文示例中给出了二维仿射变换不是线性变换，其实这是违反我对仿射变换的认知的，因为旋转、缩放、平移、错切给我的感觉就很“线性”，咋还非线性了呢。

二维仿射变换的非线性性

二维仿射变换的非线性性主要来自于平移，考虑简单的二维向量 $\textbf{p}=[x,y]^T$位移 $\Delta d$ 向量的平移变换：
$$
f(\textbf{p})=\textbf{p}+\Delta \textbf{d}
$$
那么线性变换的加法运算：
$$
f(\textbf{p} + \textbf{q})=\textbf{p}+\textbf{q}+\Delta \textbf{d}
$$
但是：
$$
f(\textbf{p}) + f(\textbf{q})=\textbf{p}+\textbf{q}+2\Delta \textbf{d}
$$
这就导致了仿射平移在二维空间上没有保持线性加法，同理标量乘法的性质也丢了：
$$
f(c\textbf{p})=c\textbf{p}+\Delta \textbf{d} \ne c(\textbf{p}+\Delta \textbf{d})=cf(\textbf{p})
$$
原点也没有映射到原点：
$$
f(\textbf{0})=\Delta \textbf{d} \ne \textbf{0}
$$
表明确实二维仿射变换在二维空间中不符合线性变换的定义。

二维仿射变换在三维空间

如果将二维平面看做是三维空间中的一个平面，结果却不一样了

二维平面看做是三维空间中 $z=1$ 的平面，那么之前二维的向量变为了 $\textbf{p}=[x,y,1]^T$，平移向量多加一维 0 值，设为 $\Delta\textbf{d} = [a,b,0]^T$，此时神奇的地方在于平移可以表示成矩阵乘法：

$$ \begin{array}{l} f(\textbf{p})&=&\textbf{p}+\Delta \textbf{d}\\ &=& \left[\begin{array}{l}x \\ y \\ 1 \end{array}\right] + \left[\begin{array}{l}a \\ b \\ 0 \end{array}\right]\\ &=&\left[\begin{array}{l}1 & 0 &a \\ 0 & 1 &b \\ 0 &0&1 \end{array}\right]\left[\begin{array}{l}x \\ y \\ 1 \end{array}\right]\\ &=&\textbf{Ap} \end{array} $$

注意：此处 $\textbf{p}+\Delta \textbf{d}$ 与 $\textbf{Ap}$ 仅在 $\textbf{p}$ 第三维为 1 时等价，也就是说对于一般的向量 $\textbf{q}=[x,y,z]^T$，$\textbf{q}+\Delta \textbf{d} \ne \textbf{Aq}$

其中：

$$ \textbf{A}=\left[\begin{array}{l}1 & 0 &a \\ 0 & 1 &b \\ 0 &0&1 \end{array}\right] $$

则这个平移操作变成了固定系数的矩阵乘法，也就是一个线性系统了：
$$
f(\textbf{p+q})=\textbf{A}(\textbf{p+q})=\textbf{Ap} +\textbf{Aq}=f(\textbf{p})+f(\textbf{q})
$$

$$
f(\textbf{cp})=\textbf{A}(c\textbf{p})=c\textbf{Ap}=cf(\textbf{p})
$$

也就是说，仿射变换表示成三维矩阵乘法后是线性变换，他是一般三维线性变换的一个特例。

参考资料

• https://www.zhihu.com/question/20666664?sort=created
• https://www.sohu.com/a/446566286_348129
• https://zhuanlan.zhihu.com/p/446758762
• https://zh.wikipedia.org/wiki/线性映射

文章链接：
https://www.zywvvd.com/notes/study/linear-algebra/linear-trans/linear-trans/