仿射变换(affine transformation)

本文最后更新于：2024年5月7日下午

简单来说，“仿射变换”就是：“线性变换”+“平移”，本文记录相关内容。

线性变换

之前我们整理过线性变换相关的知识，核心有三点：

变换前是直线的，变换后依然是直线
直线比例保持不变
变换前是原点的，变换后依然是原点

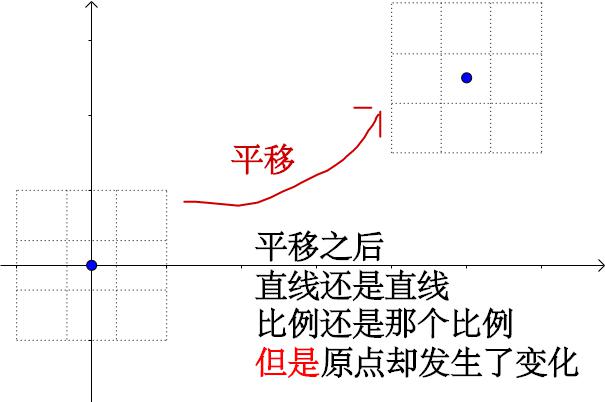
仿射变换

在线性变换中其实也提到了仿射变换，当时就定性了平面上二维仿射变换不是线性变换，因为原点会移动。

仿射变换从几何直观只有两个要点：

变换前是直线的，变换后依然是直线
直线比例保持不变

相比于线性变换就是不再保持原点的自我映射

$ A $ 为一 $ n \times n $ 阶实矩阵，对于现有 $n$ 维向量 $\textbf{x}$，针对他的仿射变换就是线性变换和平移变换的叠加，$ \mathbf{b} $ 是 $ n $ 维向量，定义于几何空间 $ \mathbb{R}^{n} $ 的仿射变换具有下列形式:
$$
T(\mathbf{x})=A \mathbf{x}+\mathbf{b}
$$
也就是说，仿射变换由一线性变换加上一平移量构成。因为 $ T(\mathbf{0})=\mathbf{b} $ 。除非平移量 $ \mathbf{b} $ 为零，仿射变换才是线性变换。仿射变换有两个特殊的性质：共线(collinearity)不变性和比例不变性，意思是 $ \mathbb{R}^{n} $ 的任一直线经仿射变换的像(image)仍是一直线，而且直线上各点之间的距离比例维持不变。

通过线性变换来完成仿射变换

$ \vec{y}=A \vec{x}+\vec{b} $ 可以写作 $ \left[\begin{array}{l}\vec{y} \\ 1\end{array}\right]=\left[\begin{array}{cc}A & \vec{b} \\ 0 & 1\end{array}\right]\left[\begin{array}{l}\vec{x} \\ 1\end{array}\right] $

即虽然在当前维度下仿射变换不是线性变换，但可以通过升维，实现通过高维线性变换完成低维仿射变换的效果。

引用马同学的解释：

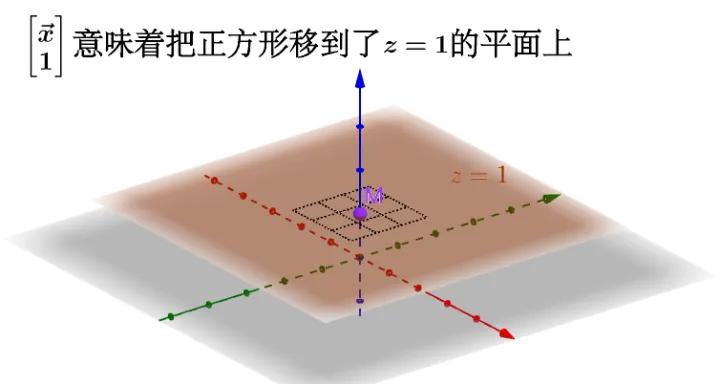
这样我就可以在二维空间下通过 $ \left[\begin{array}{cc}A & \vec{b} \\ 0 & 1\end{array}\right] $ 这个线生变换来喿作 $ z=1 $ 平面上的二维正方形，完成仿射变换：

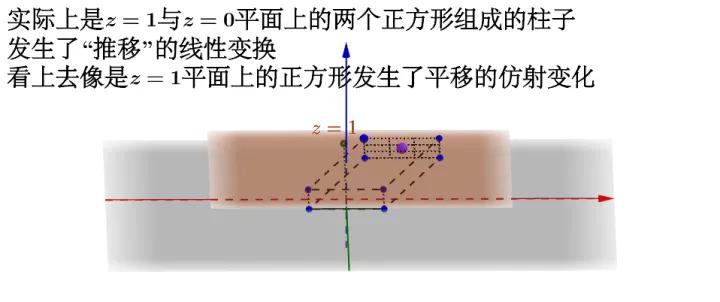
维基百科中有动图形象地揭示了这个过程：

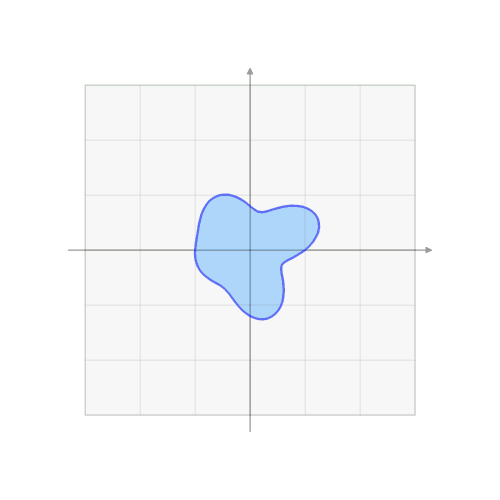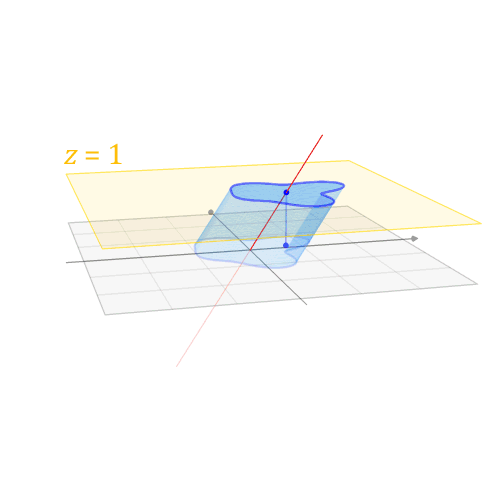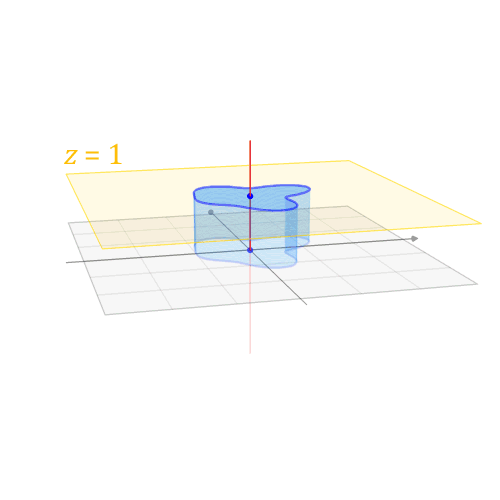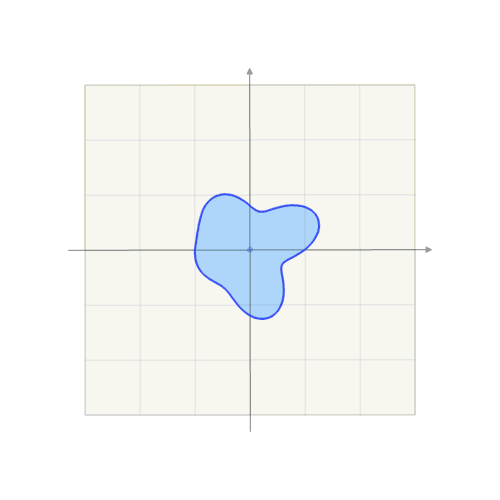
常见的仿射变换

仿射变换主要有旋转、平移、缩放、错切四种常见变换以及他们的任意组合形式。

变换名称	变换矩阵	示例
恒等变换	$\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$
平移	$\left[\begin{array}{ccc}1 & 0 & v_{x}>0 \\ 0 & 1 & v_{y}=0 \\ 0 & 0 & 1\end{array}\right]$
翻转	$\left[\begin{array}{ccc}-1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$
缩放	$\left[\begin{array}{ccc}c_{x}=2 & 0 & 0 \\ 0 & c_{y}=1 & 0 \\ 0 & 0 & 1\end{array}\right]$
旋转	$\left[\begin{array}{ccc}\cos (\theta) & -\sin (\theta) & 0 \\ \sin (\theta) & \cos (\theta) & 0 \\ 0 & 0 & 1\end{array}\right]$
错切	$\left[\begin{array}{ccc}1 & c_{x}=0.5 & 0 \\ c_{y}=0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$

求解仿射变换矩阵

我接触图像数据比较多，这里以平面仿射变换为例，高维仿射变换以此类推。

平面的仿射变换我们已经清楚，其本质就是二维线性变换叠加平移，那么未知参数就是二维线性变换的矩阵，维度为 $2\times2$，平移参数 $1\times2$，共 6 个参数

也可以理解为 $ x’ = Ax + by +C; y’ = Dx + Ey +F $，求解 6 个未知参数

对于这种情况最小需要 6 个方程用于求解，每有一对点就会获取两个方程，因此三对点可以确定一个二维仿射变换矩阵。

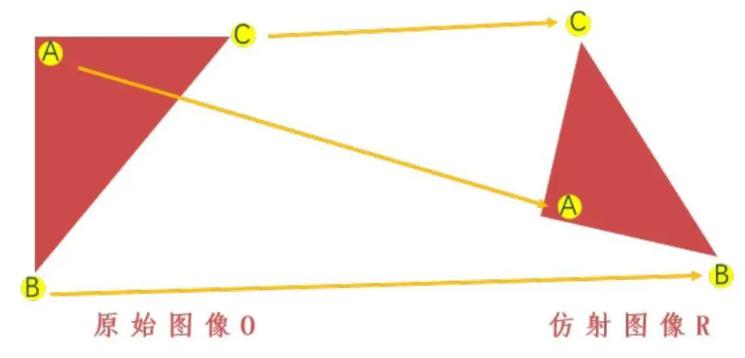
如果点对比较多，可以用最小二乘一类的方式求解，来降低误差对结果的影响。

OpenCV 实现仿射变换

OpenCV 中的仿射函数为 cv2.warpAffine() ，其通过一个变换矩阵（映射矩阵）M实现变换，具体为：
$$
dst(x, y)=src(M_{11}x+M_{12}y+M_{13}, M_{21}x+M_{22}y+M_{23})
$$
可以通过一个变换矩阵 $M$，将原始图像 $O$ 变换为仿射图像 $R$。

因此，可以采用仿射函数 cv2.warpAffine() 实现对图像的旋转，该函数的语法格式如下：

1	`dst=cv2.warpAffine(src, M, dsize [ , flags [ , borderMode [, borderValue]]])`

参数	含义
src	要仿射的原始图像
dst	仿射后的输出图像，该图像的类型和原始图像的类型相同。dsize决定输出图像的实际大小
M	2×3的变换矩阵。使用不同的变换矩阵，就可以实现不同的仿射变换
dsize	输出图像的尺寸大小
flags	插值方法，默认为`INTER_LINEAR`。当该值为`WARP_INVERSE_MAP`时，意味着 $M$ 是逆变换类型，实现从目标图像 dst 到原始图像 src 的逆变换
borderMode	边类型，默认为 `BORDER_CONSTANT`。当该值为 `BORDER_TRANSPARENT` 时，意味着目标图像内的值不做改变，这些值对应原始图像内的异常值
borderValue	边界值，默认是 0。