对数极坐标变换用于相位、尺度搜索

本文最后更新于：2022年5月21日 凌晨

Log 极坐标变换是一种坐标转换的方法，本文记录将其用于匹配圆环的尺度与相位的思想。

简介

对于二维图形，Log-polar 转换表示从笛卡尔坐标到极坐标的变化，广泛应用在计算机视觉中。此函数模仿人类视网膜中央凹视力，并且对于目标跟踪等可用于快速尺度和旋转变换不变模板匹配。

问题描述

  • 考虑已知圆形方程的圆环形态的图像$A,B$，图像之间存在关于圆心的放缩、旋转关系，如何确定二者的放缩系数 $\alpha$和旋转角度$\beta$？
A
B

解决方案

  • 求解缩放系数和旋转角度，二维空间可以搜索，这种情况下是否可以转换为关于 $x,y$ 平移的模板匹配问题呢，如果可以的话则可以之间使用 OpenCV 的模板匹配函数快速匹配。
  • 处理圆环一般会进行极坐标变换。
  • 圆环$A$，B关于圆心进行常规极坐标变换：
$$ \left\{\begin{array}{l}x_a=\rho_a \cos \theta_a \\ y_a=\rho_a \sin \theta_a\end{array}\right.,\left\{\begin{array}{l}x_b=\rho_b \cos (\theta_b) \\ y_b=\rho_b \sin (\theta_b)\end{array}\right. $$
  • 根据极坐标变换有：
$$ \rho=\sqrt{x^2+y^2}，\theta=arctan(\frac{y}{x}) $$
  • 考虑尺度变换：
$$ \rho_a=\sqrt{x_a^2+y_a^2},\rho_b=\alpha\sqrt{x_a^2+y_a^2} $$
  • 考虑角度变换：

$$
\theta_b = \theta_a+\beta
$$

  • 此时相位转换成了关于$\theta$ 的平移问题，而缩放还是相乘的关系，无法套用模板匹配

  • 但如果我们使用对数极坐标变换，此时角度不变：

    • 对于圆环 $A$ 有:

      $$ \rho_a^`=log(\sqrt{x_a^2+y_a^2}) $$

    • 对于圆环 $B$ 有：

      $$ \rho_b^`=log(\alpha\sqrt{x_a^2+y_a^2})\\ =log(\alpha)+log(\sqrt{x_a^2+y_a^2}) $$

  • 角度关系没有发生变化：

$$
\theta_b = \theta_a+\beta
$$

  • 可以看到 $\rho$ 和 $\beta$ 都转换为了需要平移搜索的变量，可以套用 OpenCV 的模板匹配

对数极坐标转换示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import mtutils as mt
import cv2
import numpy as np


def get_circle(img):
    bg = (img != 0).astype('uint8')
    bg = cv2.morphologyEx(bg, cv2.MORPH_CLOSE, np.ones([19, 19]))
    canny_res = cv2.Canny(bg * 255, 50, 150)
    Xs, Ys = canny_res.nonzero()
    ring_contours = np.stack((Xs, Ys), axis=1).astype('float32')
    ellipse, _ = mt.FitEllipse_RANSAC(ring_contours, max_itts=5, max_refines=2, graphics=True)
    center = ellipse[0][::-1]
    radius = np.mean(ellipse[1]) / 2

    return center, radius


if __name__ == '__main__':
    img_1 = mt.cv_rgb_imread('1.png', gray=True)
    circle_1 = get_circle(img_1)
    img_2 = mt.cv_rgb_imread('2.png', gray=True)
    circle_2 = get_circle(img_2)
    img_3 = mt.cv_rgb_imread('3.png', gray=True)
    circle_3 = get_circle(img_3)
    img_4 = mt.cv_rgb_imread('4.png', gray=True)
    circle_4 = get_circle(img_4)

    log_polar_res1 = cv2.warpPolar(img_1, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR + cv2.WARP_POLAR_LOG)
    log_polar_res2 = cv2.warpPolar(img_2, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR + cv2.WARP_POLAR_LOG)
    log_polar_res3 = cv2.warpPolar(img_3, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR + cv2.WARP_POLAR_LOG)
    log_polar_res4 = cv2.warpPolar(img_4, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR + cv2.WARP_POLAR_LOG)

    polar_res1 = cv2.warpPolar(img_1, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR)
    polar_res2 = cv2.warpPolar(img_2, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR)
    polar_res3 = cv2.warpPolar(img_1, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR)
    polar_res4 = cv2.warpPolar(img_2, [500, 1000], circle_1[0], 420, flags=cv2.INTER_CUBIC + cv2.WARP_POLAR_LINEAR)

    mt.PIS(img_1, img_2, img_3, img_4)
    mt.PIS(log_polar_res1, log_polar_res2, log_polar_res3, log_polar_res4)
    mt.PIS(polar_res1, polar_res2, polar_res3, polar_res4)
    pass
  • 设计四张经过缩放和旋转的圆环图像：

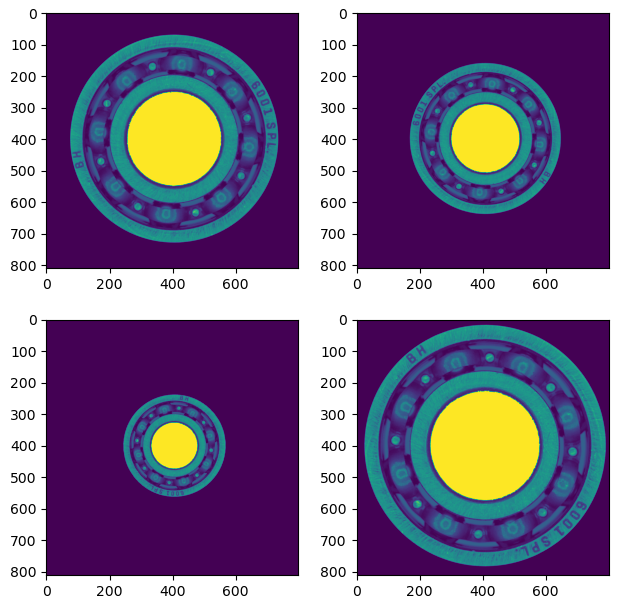
  • 正常极坐标变换后圆环宽度不同，无法平移匹配：

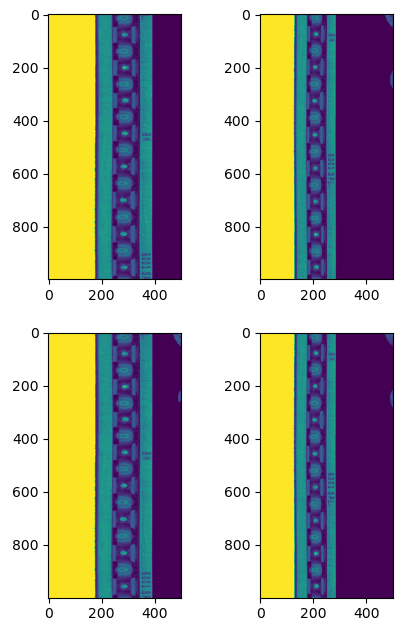
  • 对数极坐标变换后图像之间仅差平移的差距：

参考文档