本文最后更新于：2024年5月7日 下午

当分析一张图像的时候，针对轮廓，我们也许有很多事情要做。毕竟，所有轮廓都是或即将是我们想要进行识别或操作的。另外相关的还有多种对轮廓的处理，如描述轮廓，简化或拟合轮廓，匹配轮廓到模板，等等。本文记录 OpenCV 中的轮廓分析的相关操作。

多边形逼近

当我们绘制一个多边形或进行形状分析时，通常需要使用多边形逼近一个轮廓，使顶点数变少。有多种方法可以实现这个功能，OpenCV实现了其中的两种逼近方法。

Douglas-Peucker(DP) 逼近算法

  • 该算法首先从轮廓(图B)中挑出两个最远的点，将两点相连(图C)。然后在原来的轮廓上寻找一个离线段距离最远的点，
    将该点加入逼近后的新轮廓中。
  • 算法反复迭代，不断将最远的点添加到结果中，直到所有点到多边形的最短距离小于 parameter 参数指定的精度(图F)。从这里可以看出，将该精度设置为轮廓周长或外包矩形周长等表示轮廓总长度的值的几分之一比较合适。

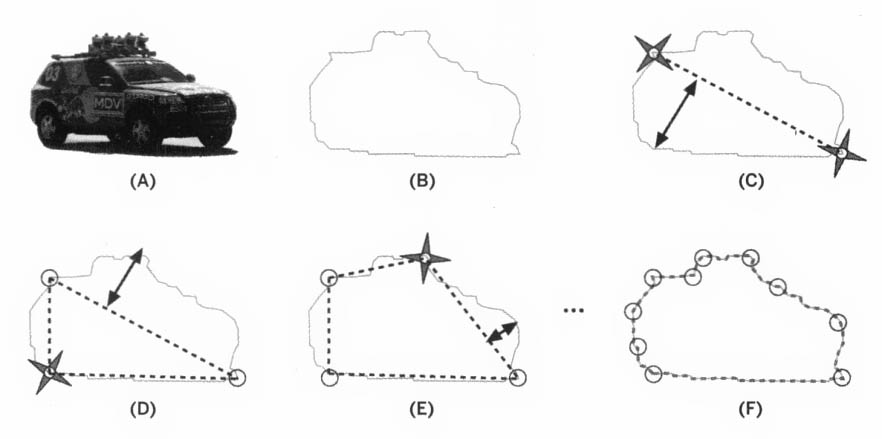
DP算法的示意图：(A)为原始图像；(B)为提取的轮廓；©表示从最远的两个点开始；(D~F)表示其他点的选择过程

cv2.approxPolyDP

以指定精度逼近多边形曲线。

官方文档

  • 函数使用
1
2
3
4
5
6
7
cv2.approxPolyDP(
	curve, 					# 输入排序的点向量
	epsilon, 				# 指定近似精度的参数。这是原始曲线与其近似值之间的最大距离。
	closed[, 				# 如果为真，则近似曲线是闭合的（它的第一个和最后一个顶点是连接的）。否则，它不会闭合。
	approxCurve]
	) ->
	approxCurve
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
img = 255 - mt.cv_rgb_imread('conc.png', gray=True)
contours, hierarchy = cv2.findContours(img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
cout_res = cv2.approxPolyDP(contours[0], 10, True)
res1 = np.zeros_like(img)
res2 = np.zeros_like(img)
cv2.drawContours(res1, [contours[0]], -1, [200], 3)
cv2.drawContours(res2, [cout_res], -1, [200], 3)
print(len(contours[0]), len(cout_res))
PIS(res1, res2)

-->

1209 14

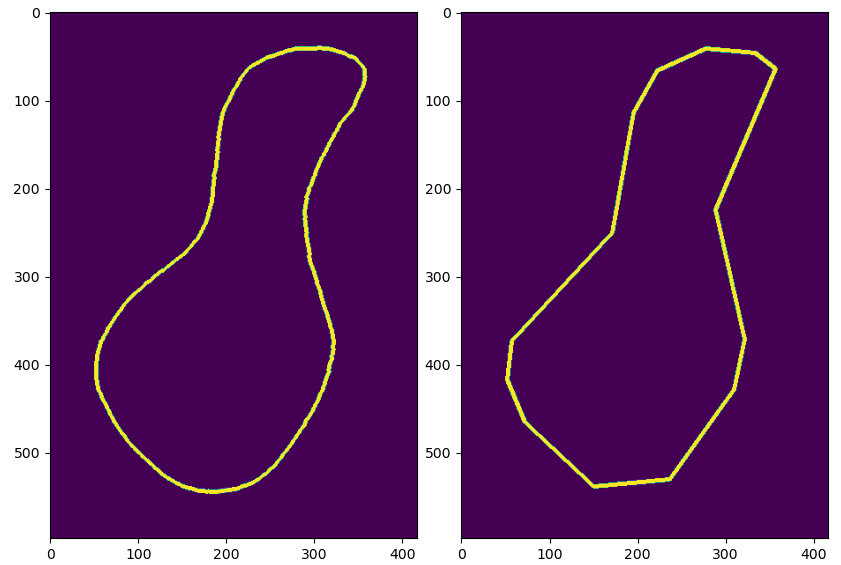
几何及特性概括

  • 轮廓处理中经常遇到的另一个任务是计算一些轮廓变化的概括特性。这可能包括长度或其他一些反应轮廓整体大小的量度。另一个有用的特性是轮廓矩(contour moment)可以用来概括轮廓的总形状特性，这部分我们在下一节讨论。以下一些方法对任何形式的点集都适用（包括那些并不代表轮廓的点集）。我们会指出哪些方法只适用于轮廓（如计算弧长），而哪些方法对任何点集都适用（如外包矩形）。

cv2.arcLength

计算轮廓周长或曲线长度。

官方文档

  • 函数使用
1
2
3
4
5
cv2.arcLength(
	curve, 				# 输入排序的点向量
	closed				# 指示曲线是否闭合的标志。
	) ->	
	retval				# 长度
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
contour = np.array([
    [[0], [0]],
    [[10], [0]],
    [[10], [10]],
    [[0], [10]]
])
length= cv2.arcLength(contour, True)

-->

length
40.0

cv2.boundingRect

  • 获得矩形包围框。当然，长度和面积只是轮廓的简单特性。描述轮廓的一种最简易的方法是为它加上一个外包围框。最简单的途径是直接计算外包围矩形。这正是 cv2.boundingRect 函数做的。
  • 该句型为正方向的矩形（不能旋转）

计算点集或灰度图像的非零像素的右上边界矩形。

官方文档

  • 函数使用
1
2
3
4
cv2.boundingRect(
	array
	) ->
	retval
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
contour = np.array([
    [[0], [0]],
    [[10], [0]],
    [[20], [10]],
    [[0], [10]]
])
bbox = cv2.boundingRect(contour)

-->

bbox
(0, 0, 21, 11)

cv2.minAreaRect

cv2.boundingRect得到的矩形框存在一个问题，只能表现一个四边水平和垂直的矩形。而函数cv2.minAreaRect可以返回一个包围轮廓最小的矩形，这个矩形很可能是倾斜的。

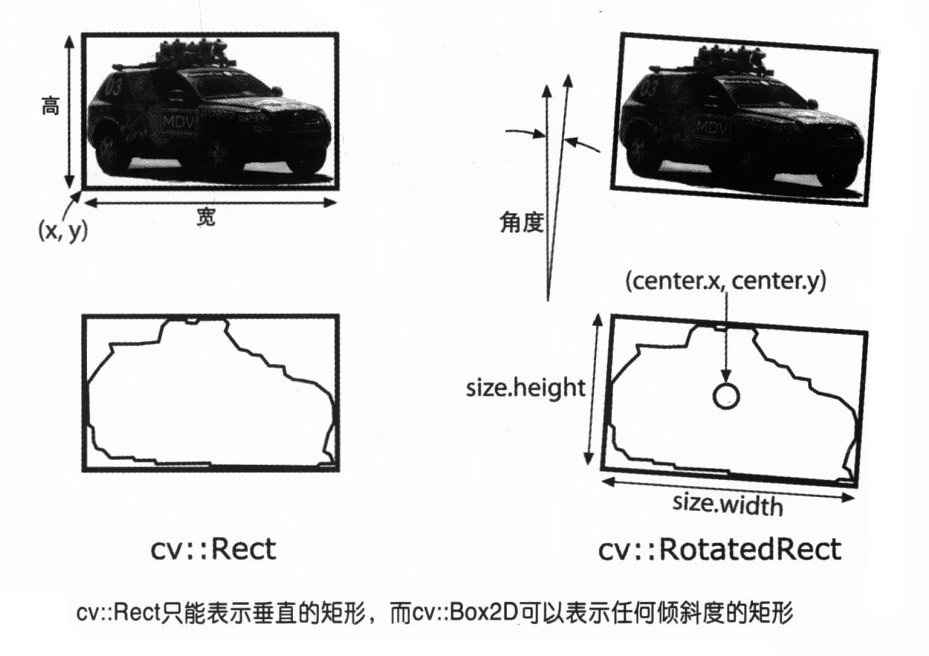
查找包含输入 2D 点集的最小区域的旋转矩形。

官方文档

  • 函数使用
1
2
3
4
cv2.minAreaRect(
	points
	) -> retval

  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
contour = np.array([
    [[5], [0]],
    [[0], [5]],
    [[10], [5]],
    [[5], [10]]
])
cv.minAreaRect(contour)

-->

((5.0, 5.000000476837158), (7.071068286895752, 7.071068286895752), 45.0)

中心，长宽，角度

cv2.minEnclosingCircle

获得最小包围圆

官方文档

  • 函数使用
1
2
3
cv2.minEnclosingCircle(
	points					# 输入点
	) -> center, radius
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
contour = np.array([
    [[5], [0]],
    [[0], [5]],
    [[10], [5]],
    [[5], [10]]
])
center, radius = cv2.minEnclosingCircle(contour)

-->
center, radius
((5.0, 5.0), 5.000100135803223)

cv2.fitEllipse

拟合椭圆

官方文档

  • 函数使用
1
2
3
4
cv2.fitEllipse(	
	points				# 输入点
	) ->	
	retval
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
contour = np.array([
    [[5, 0]],
    [[0, 16]],
    [[0, 24]],
    [[10, 16]],
    [[5, 40]],
    [[10, 24]]
]).astype('float32')
ellipse = cv2.fitEllipse(contour)
img = np.zeros([60, 30, 3], dtype='uint8')
cv2.ellipse(img, ellipse, color=[255, 255, 0], thickness=2)
PIS(img)

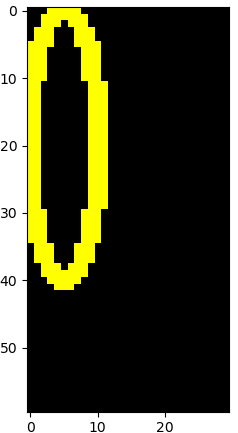
cv2.fitLine

拟合点成为一条直线

官方文档

  • 函数通过最小化 $ \sum_{i} \rho\left(r_{i}\right) $ 来拟合2D或3D的一系列点成为一条直线，其中$r_i$ 是第$i$ 个点距离直线的距离度量，$ \rho® $ 是一个距离计算函数，可以有如下的计算方式：

    官方文档

参数 计算方法
cv2.DIST_L2 $ \rho ( r )=r^{2} / 2 $ (最简单也是最快的，最小二乘法)
cv2.DIST_L1 $ \rho ( r ) =r$
cv2.DIST_L12 $ \rho ( r )=2 \cdot\left(\sqrt{1+\frac{r^{2}}{2}}-1\right) $
cv2.DIST_FAIR $ \rho ( r )=C^{2} \cdot\left(\frac{r}{C}-\log \left(1+\frac{r}{C}\right)\right) \quad where \quad C=1.3998 $
cv2.DIST_WELSCH $ \rho ( r )=\frac{C^{2}}{2} \cdot\left(1-\exp \left(-\left(\frac{r}{C}\right)^{2}\right)\right) \quad where \quad C=2.9846 $
cv2.DIST_HUBER $ \rho ( r )=\left\{\begin{array}{ll}r^{2} / 2 & \text { if } r < C \\ C \cdot(r-C / 2) & \text { otherwise }\end{array} \quad\right. $
$where \quad C=1.345$
  • 函数使用
1
2
3
4
5
6
7
8
9
10
11
12
cv.fitLine(
	points, 			# 点集列表，可以是2D也可以3D
	distType, 			# 使用的距离
	param, 				# 对于某些类型的距离，数值参数(c)。如果是0，则选择一个最佳值。
	reps, 				# 足够的半径精度（坐标原点和直线之间的距离）。
	aeps[, 				# 角度的精度，建议初始设置为 0.01 
	line]
	) ->	
	line				# 输出行参数。对于2d 拟合，它应该是一个由4个元素组成的向量(比如 Vec4f)-(vx，vy，x0，y0) ，
						  其中(vx，vy)是与直线共线的规范化向量，(x0，y0)是直线上的一个点。
						  对于3d 拟合，它应该是一个由6个元素组成的向量(比如 Vec6f)-(vx，vy，vz，x0，y0，z0) ，
						  其中(vx，vy，vz)是与直线共线的规范化向量，(x0，y0，z0)是直线上的一个点。
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
contour = np.array([
    [[5, 5]],
    [[14, 16]],
    [[28, 24]],
    [[10, 11]],
    [[42, 40]],
    [[31, 34]]
]).astype('int32')
line = cv2.fitLine(contour, cv2.DIST_L2, 0, 0.01, 0.01)
pt1 = mt.vvd_round(((line[2] - 100*line[0])[0], (line[3] - 100*line[1])[0]))
pt2 = mt.vvd_round(((line[2] + 100*line[0])[0], (line[3] + 100*line[1])[0]))

img = np.zeros([50, 50, 3], dtype='uint8')

img = cv2.line(img, pt1, pt2, [255, 255, 0], 1)
img[contour[:,0,0], contour[:,0,1], 2] = 255
PIS(img)

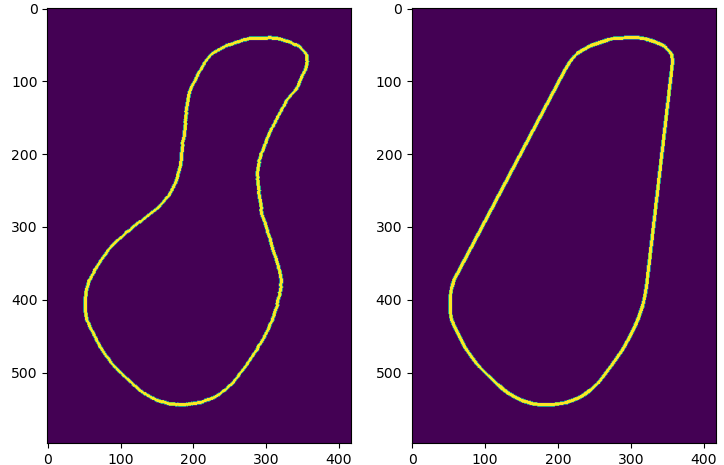
cv2.convexHull

计算轮廓凸包

官方文档

  • 函数使用
1
2
3
4
5
6
7
8
cv2.convexHull(
	points[, 				# 2D 点集
	hull[, 					# 输出凸包
	clockwise[, 			# 方向标志。如果为真，则输出凸包为顺时针方向。
							  否则，它是逆时针方向的。假设坐标系的 x 轴指向右侧，y 轴指向上方。
	returnPoints]]]			# 操作标志。对于矩阵，当标志为真时，函数返回凸包点。否则，它返回凸包点的索引。
	) ->
	hull
  • 示例代码
1
2
3
4
5
6
7
8
9
img = 255 - mt.cv_rgb_imread('conc.png', gray=True)
contours, hierarchy = cv2.findContours(img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
hull = cv2.convexHull(contours[0])
res1 = np.zeros_like(img)
res2 = np.zeros_like(img)
cv2.drawContours(res1, [contours[0]], -1, [200], 3)
cv2.drawContours(res2, [hull], -1, [200], 3)

PIS(res1, res2)

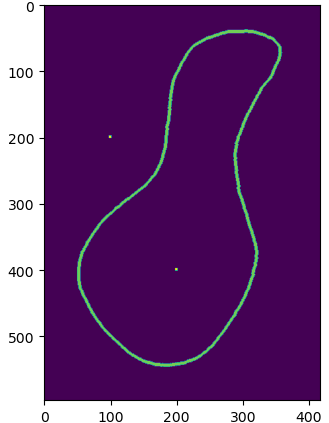
几何学测试

cv2.pointPolygonTest

判断点是否在轮廓内部

官方文档

  • 函数使用
1
2
3
4
5
6
cv2.pointPolygonTest(
	contour, 				# 轮廓
	pt, 					# 测试点
	measureDist				# 如果为真，该函数估计从点到最近等高线边缘的有符号距离。否则，该函数只检查点是否在等高线内。 
	) ->	
	retval
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
img = 255 - mt.cv_rgb_imread('conc.png', gray=True)
contours, hierarchy = cv2.findContours(img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
hull = cv2.convexHull(contours[0])
point_in = [200, 400]
point_out = [100, 200]
res1 = np.zeros_like(img)
res1[point_in[1]-2:point_in[1]+2, point_in[0]-2:point_in[0]+2] = 255
res1[point_out[1]-2:point_out[1]+2, point_out[0]-2:point_out[0]+2] = 255
cv2.drawContours(res1, [contours[0]], -1, [200], 3)
print(cv2.pointPolygonTest(contours[0], point_in, False))
print(cv2.pointPolygonTest(contours[0], point_out, False))
PIS(res1)

-->
1.0
-1.0

cv2.isContourConvex

函数用于判断轮廓是否为凸。判断一条轮廓是否为凸轮廓是常见的需求。这样做的理由很多，其中最常见的是许多算
法只能用于凸多边形，还有许多算法在多边形为凸时可以大大简化。

官方文档

  • 函数使用
1
2
3
4
cv2.isContourConvex(
	contour				# 轮廓
	) ->	
	retval
  • 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
img = 255 - mt.cv_rgb_imread('conc.png', gray=True)
contours, hierarchy = cv2.findContours(img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
hull = cv2.convexHull(contours[0])
res1 = np.zeros_like(img)
res2 = np.zeros_like(img)
cv2.drawContours(res1, [contours[0]], -1, [200], 3)
cv2.drawContours(res2, [hull], -1, [200], 3)
print(cv2.isContourConvex(contours[0]))
print(cv2.isContourConvex(hull))

-->

False
True

源码

https://github.com/zywvvd/Python_Practise/tree/master/OpenCV/Chapter 14

参考资料

  • 《学习OpenCV》 第十四章


文章链接：
https://www.zywvvd.com/notes/study/image-processing/opencv/opencv-contours-ana/contours-ana/

“觉得不错的话，给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信二维码

微信支付

支付宝二维码

支付宝支付

Image_Processing > OpenCV
#OpenCV #Image_Processing
OpenCV 轮廓 —— 轮廓分析
https://www.zywvvd.com/notes/study/image-processing/opencv/opencv-contours-ana/contours-ana/
作者
Yiwei Zhang
发布于
2022年4月23日
许可协议