机器视觉 —— 光信号检测

本文最后更新于：2023年12月5日下午

本文记录《机器视觉》第二章图像成像原理相关内容，主要介绍数字图像是如将光线转换为信号的。

信号检测

几乎所有图像传感器的工作原理都依赖于：光子击打某种特殊材料时所产生的“电子/空穴”对。这是生物视觉和摄影的基本过程。
不同的图像传感器之间的区别在于：它们对带电粒子流的检测方式不同。

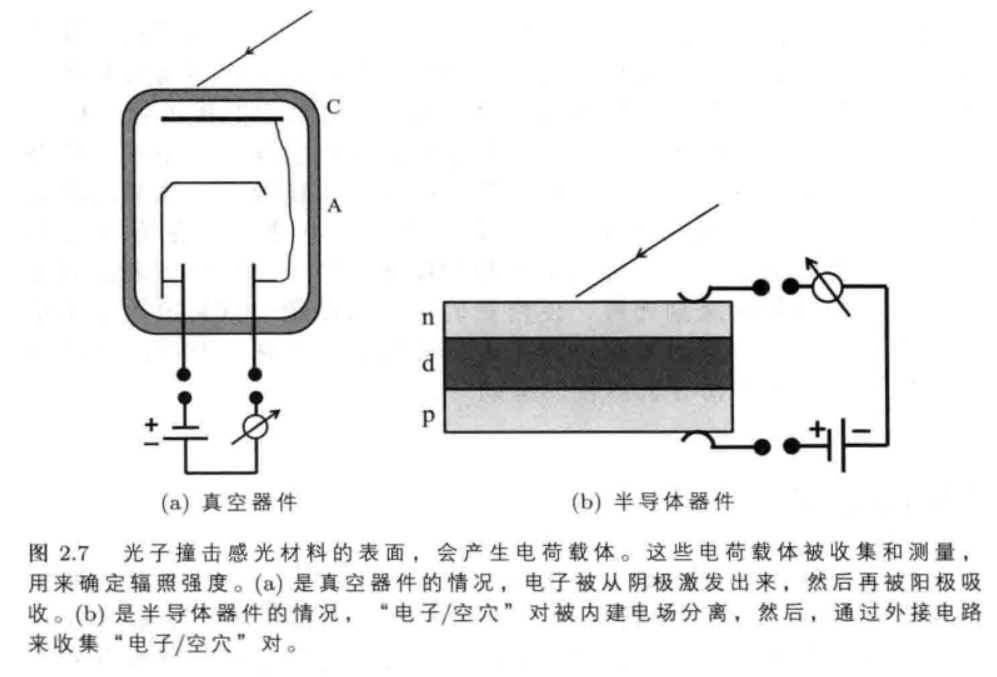
一些仪器使用真空中的电场来分离从材料表面释放出来的自由电子(如图(a)所示）：而在另一些仪器中，被激发出来的电子将击穿半导体中的耗尽层(如图(b)所示）

并不是所有的入射光子都会产生“电子/空穴”对。一些电子正好在感应层中传播，一些被反射回来，或者，以其他形式将其能量损失掉了。此外，并不是所有的电子都能正好进入检测电路。电子流和入射光子流的比值称为量子效率，记为$q(\lambda)$。量子效率依赖于入射光子的能量，因此，它依赖于入射光的波长$\lambda$。同时，量子效率还依赖于：1)材料，以及，2)仪器收集自由电子的方式。真空仪器上的涂料具有相对较低的量子效率。对于某些特定波长，固态电子器件近乎为理想器件。摄影胶片的量子效率很低。

感知颜色

仪器的灵敏度和入射光的波长有关。具有很大能量的光子会直接进入材料，而能量太小的光子可能在到达材料表面前就被拦截。每一种材料都有属于其自身的、随光的波长而变化的量子效率特征。对于一个很小的波长区间$ \delta \lambda $，令$ b(\lambda) \delta \lambda $表示：能量大于等于$ \lambda$而小于$ \lambda+\delta \lambda $的光子流，那么，材料表面所释放出的自由电子数目为：
$$
\int_{-\infty}^{\infty} b(\lambda) q(\lambda) d \lambda
$$
如果我们使用：由不同光敏材料做成的（图像）传感器，那么，我们将会得到不同的图像，因为传感器的光谱灵敏度不同。对于某一个曲面，假设：当我们用不同的传感器对其进行成像时，所得到的图像的灰度值不同：那么，我们可以利用这个结果来进行辨别。另一种获得这种效果的方法是：使用相同的感光材料，但是，在相机前放上滤光镜。滤光镜会对光谱中的不同频率成分进行选择性吸收。如果第$i$个滤光镜的透光率为$f_i(\lambda)$，那么滤光镜和传感器组合在一起的等效量子效率为$f_i(\lambda)q(\lambda)$。

随着所使用的滤光镜数目的增加，对材料的辨别能力也会增加。但是，这些测量结果是相关的，这是因为：对于绝大多数材料，其反射率随入射光的改变而发生“光滑”变化。一般情况下，使用太多的滤光镜并不能有效地提高对材料的辨别能力。

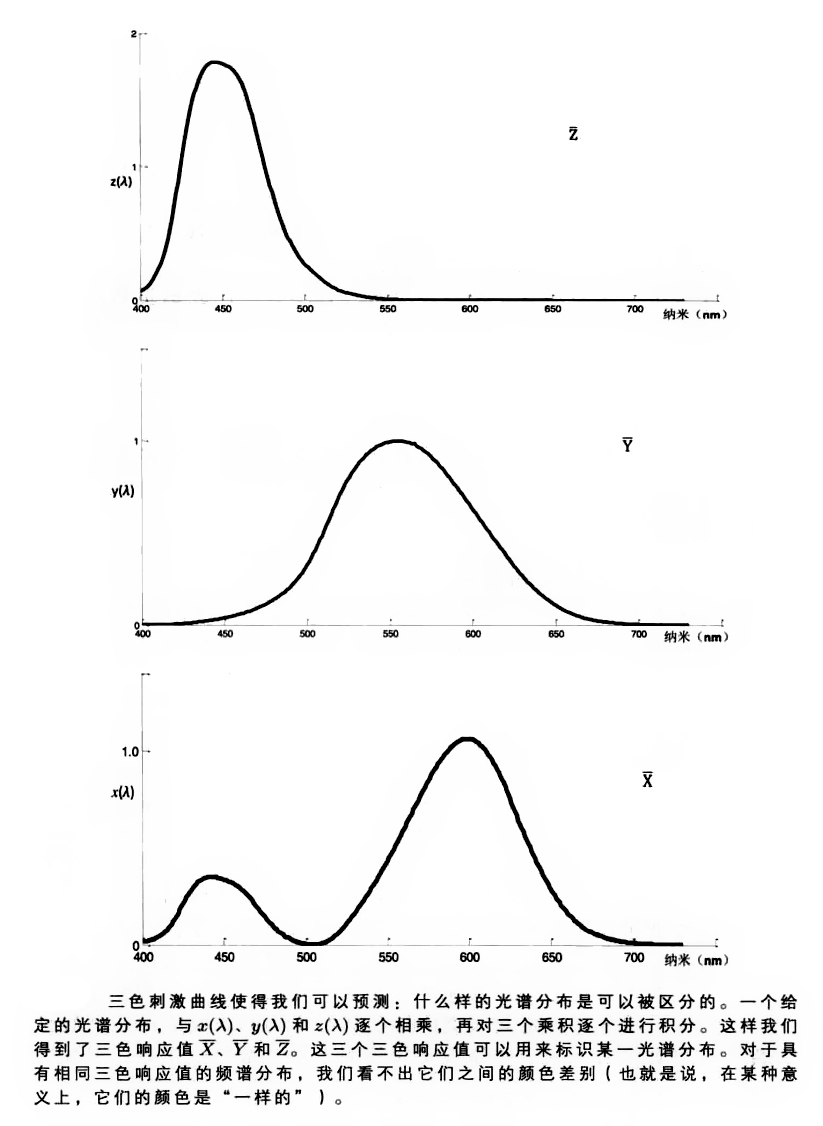
在白光条件下，人类视觉系统所使用的“传感器”有三种。这些“传感器”被称为：锥状体。这三种锥状体中的每一种都具有特殊的光谱灵敏度。一种锥状体主要用于感知：可见光谱（其范围从400纳米到700纳米）中的长波长区；一种锥状体主要用于感知：可见光谱中的中波长区：第三种锥状体主要用于感知：可见光谱中的短波长区。这三种锥状体的感应曲线之间有相当大的重合。

机器视觉系统使用红、绿、蓝三种滤光镜来获得图像。但是，需要指出的是：这种“选择方式”和人类的颜色感知方式没有任何关系：除非红、绿、蓝三种滤光镜的光谱响应曲线正好是：人类的三种锥状体的光谱响应曲线的线性组合。

随机性和噪声

信号测量过程中所产生的随机“起伏”会影响我们所得到的测量结果。我们进行重复测量，可能会得到不同的结果。通常，测量结果会聚集在一个“正确”结果的周围。我们可以讨论：一个测量值落在某一个区间范围内的概率。粗略地说，就是当试验次数趋于无穷大时，测量值属于这个区间的实验次数与实验总次数之间的比值。这个定义并不精确。因为，任何一个特殊的试验序列的结果都可能不趋于我们所期望得到的极限。但是，这些结果不会远离这个极限。事实上，这个事件发生的概率为0。

定义概率密度分布$p(x)$,即：当 $ \delta x $ 趋于 0 时，随机变量大于等于$x$而小于$x+\delta x$的概率趋近于$p(x)dx$。从有限次试验结果的统计直方图中，我们可以估计出一个概率分布。

从上面的关于概率分布的定义中，我们可以看出：任何概率分布函数$p(x)$都必须具有如下两个重要性质，即：

非负性，也就是说，$p(x)≥0$
归一性，也就是说: $ \int_{\infty}^{\infty} p(x) d x=1 $

定义均值：
$$
\mu \int_{\infty}^{\infty} p(x) d x=\int_{\infty}^{\infty} x p(x) d x
$$

$$
\mu=\int_{\infty}^{\infty} x p(x) d x
$$

如果测量结果中的“噪声”是独立的，并且，它们之间相互抵消，那么，提高测量精度的一个方法是：对多次测量的结果取平均。为了理解其中的原理，我们需要知道：如何计算多个随机变量的和的概率分布。假设：

$x$是两个独立随机变量$x1$和$x2$的和
$x_1$和$x_2$的概率密度函数分别是$p_1(x_1)$和$p_2(x_2)$

那么我们如何确定$x=x_1+x_2$的概率密度函数$p(x)$呢？给定 $x_2$ 以后，由于$x$的值介于$x$和$x+\delta x$之间，因此，$x_1$的值一定介于$x-x_2$和$x+\delta x-x_2$之间。这个事件发生的概率是$p_1(x-x_2)\delta x.$

现在，$x_2$ 可以取一系列的值，并且，$x_2$ 的值位于从 $x_2$ 到 $x_2+\delta x_2$ 的区间的概率为 $p_2(x_2)δx_2$。为了得到：$x$ 的值位于从$x$ 到$x+\delta x$的区间的概率，我们必须在整个 $x_2$ 的取值范围内，对 $p_1(x-x_2)δx$ 和 $p_2(x_2)\delta x_2$ 的乘积进行积分，也就是说：
$$
p(x) \delta x=\int_{\infty}^{\infty} p_{1}\left(x-x_{2}\right) \delta x p_{2}\left(x_{2}\right) d x_{2}
$$
可以进一步写为：
$$
p(x)=\int_{\infty}^{\infty} p_{1}(x-t) p_{2}(t) d t
$$
类似地，也可以得到：
$$
p(x)=\int_{\infty}^{\infty} p_{2}(x-t) p_{1}(t) d t
$$
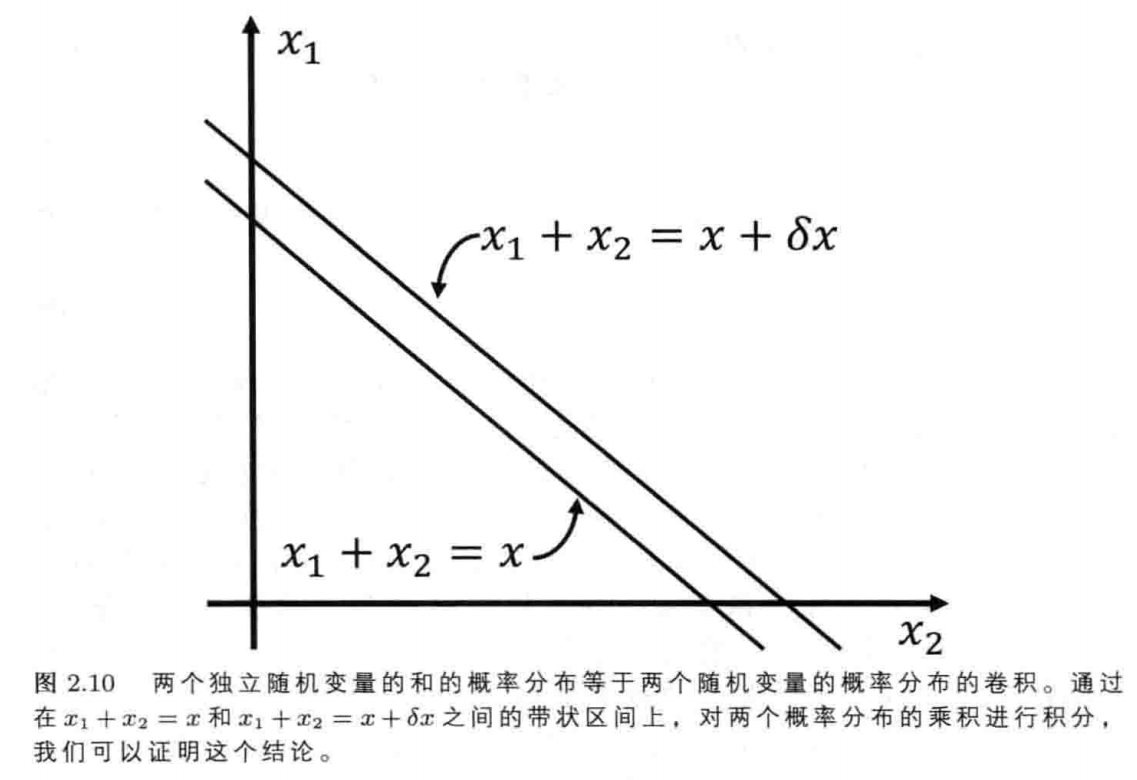
也就是说，$x_1$和$x_2$所扮演的“角色”是可以互换的。这种“互换”对应于：在一条倾斜的窄带上，使用两种不同的积分方式，对概率乘积
进行积分。对于每一种方式，我们讨论的都是：两个概率密度分布 $p_1$ 和 $p_2$ 的卷积，记为：
$$
p(x)=p_{1}(x) \otimes p_{2}(x)
$$

现在，让我们来考虑：在一个固定的时间段内，由落在某种材料表面的光子所激发出来的电子数目。这些事件（即：不同时间段内激发出来的电子数目）彼此之间是独立的。实验说明，在某一时间段 $T$ 内激发出$n$个电子的概率可以用泊松分布近似：

$$ P_n=e^{-m}\frac{m^n}{n!} $$

这个概率由一个参数$m$所决定。我们可以用如下方法来计算时间段$T$内所激发出的电子的平均数:
$$
\sum_{n=1}^{\infty} n e^{-m} \frac{m^{n}}{n !}=m e^{-m} \sum_{n=1}^{\infty} \frac{m^{(n-1)}}{(n-1) !}
$$
但是，注意：
$$
\sum_{n=1}^{\infty} \frac{m^{(n-1)}}{(n-1) !}=\sum_{n=0}^{\infty} \frac{m^{n}}{n !}=e^{m}
$$
因此，在时间段$T$内激发出的电子的平均数为$m$。

在$\delta t$时间内，从面积$\delta A$的区域内所激发出来的电子数为：
$$
N=\delta A \delta t \int_{-\infty}^{\infty} b(\lambda) q(\lambda) d \lambda
$$
其中，$q(\lambda)$表示量子效率，$b(\lambda)$表示图像辐照强度（即：单位面积上的光子数）。为了得到有用的结果，我们需要在一定的时间段内，从一定大小的区域上收集电子。因此，我们需要在（时间和空间上的）分辨率与精确性之间寻求一种平衡。

对于具有固定频谱分布的入射光，在一个固定的时间段内，我们所测量到的、从某一微小区域上被激发出的电子数目，和图像辐照强度成正比。这些测量结果需要被量化，以便于用计算机进行读取和处理。我们通过模数转换器(A/D)来实现量化过程。量化结果被称为灰度。我们难以精确测量图像辐照强度，因此，我们使用一个小的“数集”来表示图像辐照强度的“水平”。通常，我们所选用的数集为：从0到255的整数。因此，我们只需要使用8位字符来表示灰度。

图像量化

我们只能传送有限数量的测量结果给计算机，因此，我们需要对空间进行量化。通常，我们测量：矩形光栅结点上的灰度值。这样，图像就被表示成一个由整数构成的矩形数组。为了获得足够精细的图像，我们需要很多测量结果，这些结果中最小的图像数据单元称为像素。

矩形数组中的每一个数所表示的是：对应的小区域上的平均辐照强度。我们无法测量出：图像中某一点的辐照强度，因为，正如我们前面所讨论的，光通量和感应区域的面积成正比。乍一看，我们可能会觉得这似乎是一个“缺点”，但是，这最终会变成一个“优点”。这是因为：我们试图用一个离散数集去表示亮度的连续分布模式，采样定理告诉我们：只有在该连续分布函数足够光滑（也就是说，不包含高频分量）的条件下，这样做才是可行的。将亮度分布变光滑的一种方法是：用低通滤波器对其进行滤波。而低通滤波器正好对应于：对一个小区域上的灰度值取平均。

采样区域取多大最好呢？一个合理的选择方法是：让采样区域的大小和区域之间的间隔近似相等。这样做的优点是：我们能有效地在像平面上放置感应元件，从而使得：既不会造成对所需光子的“浪费”，又不会造成近邻区域之间的相互重叠。

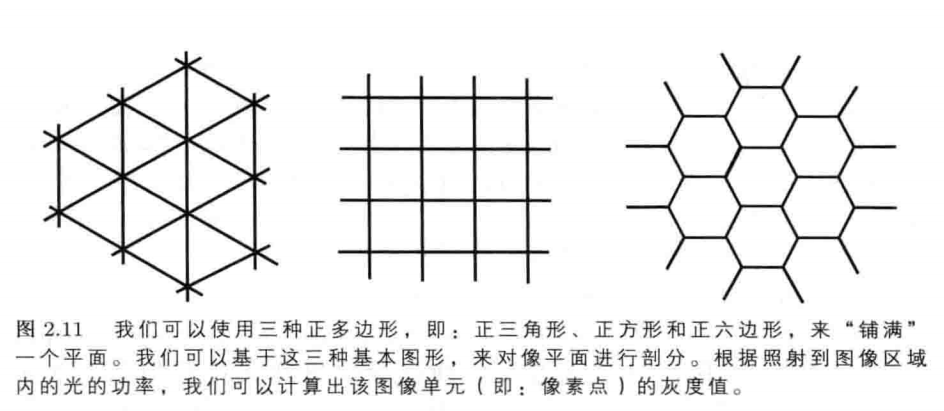
我们可以用一些边界线将像平面分割成许多小的感应区域。到目前为止，我们已经讨论了：用矩形网格将像平面分割成许多小的矩形区域的情况。在这种情况下，图像单元是完全相同的矩形，这会形成在横向和纵向上的不同分辨率。我们也可以采用其他的分割方法。假设我们想将像平面分割成许多全等的正多边形，并且，我们希望：这些正多边形之间既不存在相互覆盖，也没有“空隙”（也就是说，将这些正多边形放到一起，恰好能“完美”地覆盖整个像平面）。这样的分割方法只有三种，分别基于：

正三角形，
正方形，
正六边形。

我们容易看出：矩形采样模式的实现方法，即：沿着图像上等间隔的“线”上的等间隔的小区间来测量辐照强度。正六边形采样模式也几乎同样简单，只需让基数编号的“线”，相对于偶数编号的“线”，左右平移半个小区间。电视扫描采用隔行扫描的方式，也就是说，在扫描完所有偶数编号的“线”以后，才开始对基数编号的“线”进行扫描。因此，基于正六边形的采样模式特别容易实现。正三角形网格上的正六边形结构具有特殊的优点，我们后面将对其进行详细讨论。