OpenCV 图像分析之 —— 频域变换

本文最后更新于：2023年8月2日下午

图像可以转换到其他空间进行分析和处理，本文记录 OpenCV 分析算子中的频域变换相关内容。

离散傅里叶变换

定义

对于任意以离散参数为索引的数值集合，都可以通过与连续傅里叶变换相似的方法来定义离散傅里叶变换(DFT)。对于$N$个复数$ {x_{0}, x_{1}, x_{2}, /ldots, x_{N-1}} $,一维 DFT 由如下公式(其中$ i=/sqrt{-1} $):

$$
g_{k}=\sum_{n=0}^{N-1} f_{n} e^{-\frac{2 \pi i}{N} k n}
$$

相似的，对于二维数值数组，也可以定义变换：

$$
g_{k_{x}, k_{y}}=\sum_{n_{x}=0}^{N_{x}-1} \sum_{n_{y}=0}^{N_{y}-1} f_{n_{x}, n_{y}} e^{-\frac{2 \pi i}{N}\left(k_{x} n_{x}+k_{y} n_{y}\right)}
$$

一般计算项数为$N$的的变换预计需要$O(N^2)$次运算。实际上，有几种快速傅里叶变换(FFT)算法可以在的复杂度内计算这些值。

cv2.dft()

计算矩阵的离散傅里叶变换

函数使用

cv2.dft()函数实现离散傅里叶变换以及其逆变换(取决于flags参数)。源矩阵src必须是一维或二维的。结果矩阵dst将具有与src相同的类型和尺寸。

参数flags是一个位域值，可以设置为cv2.DFT_INVERSE,cv2.DFT_ROWS,cv2.DFT_SCALE,cv2.DFT_COMPLEX_OUTPUT或cv2.DFT_REALOUTPUT中的一个或多个。

1	`cv2.dft(src, flags=0, nonzeroRows=0)`

flags 说明
- 如果设置为cv2.DFT_INVERSE,则完成逆变换。
- 如果设置标志为cv2.DFT_ROWS,则二维n×m输入被视为长度为m的n个不同的一维向量，并且每个这样的向量将独立变换。
- 标志cv2.DFT_SCALE通过将结果除以矩阵中的元素数来标准化结果，这通常用于DFT_INVERSE,因为它保证逆的逆将具有正确的标准化。
- 标志cv2.DFT_COMPLEX_OUTPUT:和cv2.DFT_REAL_OUTPUT是有用的，因为当计算实数矩阵的傅里叶变换时，结果将有复共轭对称性。因此，即使结果是复数，结果矩阵的元素数量等于输入矩阵中的元素数量，而不是该数量的两倍。这样的压缩是cv2.dft()的默认行为。
- 若要强制输出复数的形式，则需设置标志cv2.DFT_COMPLEX_OUTPUT。在逆变换的情况下，输入（通常）为复数，输出也为复数。然而，如果输入矩阵（对逆变换的情况）具有复共轭对称性(例如，如果它本身是实数矩阵的傅里叶变换的结果)，那么逆变换将是一个实数矩阵。如果知道是这种情况，并且希望结果矩阵表示为一个实数矩阵（从而使用一半的内存量），则可以设置cv2.DFT_REAL_OUTPUT标志。
- 请注意，如果设置cv2.DFT_REAL_OUTPUT标志，cv2.dft()不会检查输入矩阵是否具有必要的对称性，它只是假定具有对称性。
nonzeroRows

cv2.dft()的最后一个参数是nonzeroRows,它默认为0，但如果设置它为任何非0值，将导致cv2.dft()认为只有输入矩阵的前nonzeroRows行是有意义的。如果cv2.DFT_INVERSE被设置，那么就认为只有输出矩阵的前nonzeroRows行是非零的。在使用cv2.dft()计算卷积的互相关时，这个标志特别方便。
最佳尺寸

cv2.dft()的性能很大程度上取决于传递给它的矩阵的确切尺寸，这种关系（性能与尺寸的关系）并不是线性的。只有一些尺寸是比其他尺寸表现出的性能更好。建议在将矩阵传递给cv2.dft()时，首先在比当前矩阵大的尺寸中确定最佳尺寸，然后将矩阵扩展为该尺寸。OpenCV提供了一个合适的例程来计算这个值，称为cv2.getOptimalDFTSize()。
示例代码

image = mt.cv_rgb_imread('img1.jpg')
image = mt.image_resize(image, [300, 300]).astype('float32')
image = mt.to_gray_image(image)

dft_res = cv2.dft(image)
inverse_img = cv2.dft(dft_res, flags=cv2.DFT_INVERSE)

PIS(image, dft_res, inverse_img)

cv2.idft()

计算矩阵的离散傅里叶逆变换，cv2.idft()只是离散傅里叶逆变换的一个方便的简写。对cv2.idft()的调用实际上相当
于调用带参数的cv2.dft(src, flags=cv2.DCT_INVERSE)

image = mt.cv_rgb_imread('img1.jpg')
image = mt.image_resize(image, [300, 300]).astype('float32')
image = mt.to_gray_image(image)

dft_res = cv2.dft(image)
res = cv2.idft(dft_res)
PIS(res)

cv2.mulSpectrums()

方法实现频谱复数元素逐元素乘积

官方文档

函数使用

cv2.mulSpectrums(
	a, 				# 第一个输入矩阵
	b, 				# 第二个输入矩阵，需要和 a 相同尺寸
	flags[, 		# 仅支持 cv2.DFT_ROWS, 表示 a 和 b 的每一行都是一个独立的一维傅里叶谱, 否则输入0
	c[, 
	conjB]]) ->c	# 在乘法执行前是否共轭虚部

其中 $a, b$ 为变量，同时为单通道频谱或双通道复数频谱

示例代码

a = np.array([[[1, 1], [1, -1]]], dtype='float32')
b = np.array([[[2, 1], [1, -2]]], dtype='float32')
mul_res = cv2.mulSpectrums(a, b, 0)


-->
mul_res
array([[[ 1.,  3.],
        [-1., -3.]]], dtype=float32)

表示复数 $(1+i, 1-i)$ 与 $(2+i, 1-2i)$ 逐元素乘积。

离散余弦变换

定义

$$ c_{k}=\left(\frac{1}{N}\right)^{\frac{1}{2}} x_{0}+\sum_{n=1}^{N-1}\left(\frac{2}{N}\right)^{\frac{1}{2}} x_{n} \cos \left(\left(k+\frac{1}{2}\right) \frac{n}{N} \pi\right) $$

用于实信号的频域分析
DCT 变换的由来

cv2.dct()

计算矩阵的离散余弦变换

函数使用

该函数根据flags参数的值执行离散余弦变换或离散余弦逆变换。源矩阵src必须是一维或二维的，并且尺寸应该是偶数(如果需要，可以填充矩阵)。结果矩阵dst将具有与src相同的类型和尺寸。参数flags是一个位域值，可以设置为cv2.DCT_INVERSE或cv2.DCT_ROWS中的一个或两个。

1	`cv2.dct(src, flags) --> dst`

参数说明
- src 需要为一维或二维的 float32 或 float64 数据
- flags 不设置默认正向变换
- flags 如果设置为cv2.DCT_INVERSE,则实现逆变换而不是前向变换。
- flags 如果设置标志为cv2.DCT_ROWS,则将二维n×m的输入视为长度为m的n个不同的一维向量。在这种情况下，每个这样的向量将被独立地变换。
最佳尺寸

cv2.dct() 的性能很大程度上取决于传递给它的矩阵的确切尺寸，这种关系（性能与尺寸的关系）并不是单调的。只有一些尺寸是比其他尺寸表现出的性能更好。建议在将矩阵传递给 cv2.dct() 时，首先在比当前矩阵大的尺寸中确定最佳尺寸，然后将矩阵扩展为该尺寸。OpenCV 为你提供了一个合适的例程来计算这个值，称为 cv2.getOptimalDFTSize()。
示例代码

image = mt.cv_rgb_imread('img1.jpg')
image = mt.image_resize(image, [300, 300]).astype('float32')
image = mt.to_gray_image(image)

dct_res = cv2.dct(image)
inverse_img = cv2.dct(dct_res, flags=cv2.DCT_INVERSE)

PIS(image, (dct_res*150).astype('uint8'), inverse_img.astype('uint8'))

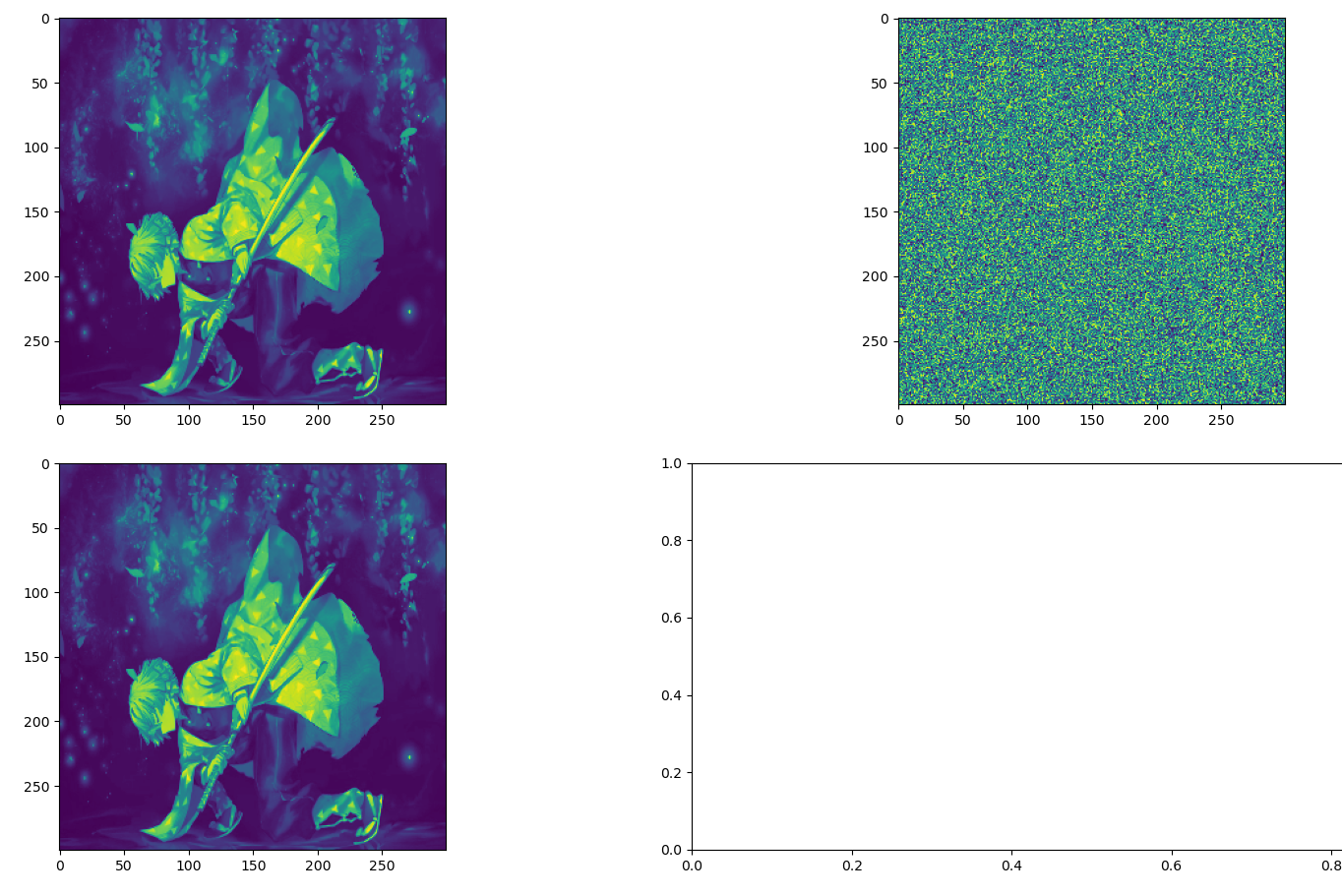
cv2.idft()

计算矩阵的离散傅里叶逆变换，cv2.idft()只是离散傅里叶逆变换的一个方便的简写。对cv2.idft()的调用实际上相当
于调用带参数的cv2.dft(src, flags=cv2.DCT_INVERSE)

image = mt.cv_rgb_imread('img1.jpg')
image = mt.image_resize(image, [300, 300]).astype('float32')
image = mt.to_gray_image(image)

dft_res = cv2.dft(image)
res = cv2.idft(dft_res)
PIS(res)