本文最后更新于:2024年5月7日 下午
本文摘录 OpenCV 中的图像变换相关操作内容,重点介绍 Opencv 中的拉伸、收缩、扭曲和旋转操作。
概述
图像变换最直接的应用就是改变图像的形状、大小、方向等等,这些在OpenCV 中有部分现成的实现。
-
文中示例为Python代码,用到了我常用的工具库
mtutils,文中用到的该库内容主要为opencv和matplotlib库的封装,可以用命令1
pip install mtutils安装该库
-
使用时可以按照如下方式引入:
1
2
3
4
5
6
7
8
9import mtutils as mt
mt.PIS(img)
mt.cv_rgb_imread(img_path)
# 或
from mtutils import PIS, cv_rgb_imread
PIS(img)
cv_rgb_imread(img_path)
均匀调整
图像放缩
我们经常遇到一些尺寸的图像,我们想转换成其他尺寸。我们可能想要增大或缩小图像,这两个任务都是可以通过相同的函数实现的。
cv2.resize()
- 函数使用
1 | |
-
参数说明
dsize和fx,fy只能配置一套,即要么配置尺寸,要么配置比例,二者互斥- 如
dsize为None,则其计算方法为:
$$
dsize =\operatorname{Size}( round (f x· \operatorname{src} . cols ) , round (fy·src.rows))
$$- 如
fx,fy为 0,则其计算方法为:
-
interpolation
可选值 含义 cv2.INTER_NEAREST 最近邻插值 cv2.INTER_LINEAR 双线性插值 cv2.INTER_CUBIC bicubic 插值 cv2.INTER_AREA 基于像素面积关系的重采样。这可能是图像抽取的首选方法,因为它给出了无云纹的结果。但是当图像缩放时,它类似于 cv2.INTER_NEAREST方法。cv2.INTER_LANCZOS4 在8x8的邻域兰克左斯插值 cv2.INTER_LINEAR_EXACT 精确的双线性我 cv2.INTER_MAX 插补代码的掩码 cv2.WARP_FILL_OUTLIERS 填充所有目标图像像素。如果其中一些对应于源图像中的异常值,则将其设置为零 cv2.WARP_INVERSE_MAP 反变换插值 -
示例代码
1 | |

图像金字塔
图像金字塔广泛应用于各种视觉应用中。图像金字塔是图像的集合,它由单个原始图像产生,连续降采样,直到达到一些期望的停止点。此停止点可能是单像素图像!
- 文献和应用中经常出现两种图像金字塔:高斯和拉普拉斯金字塔。高斯金字塔用于降采样图像,当我们要从金字塔中较低的图像重构上采样图像时,需要拉普拉斯金字塔。
cv2.pyrDown()
模糊图像并对其进行采样。
-
通常,我们通过首先将层$G_i$与高斯核卷积,然后去除每个偶数行和列,从而生成金字塔的层$G_i$生成高斯金字塔(我们表示该层$G_{i+1}$)中的层$(i+1)$。当然,在这种情况下,每个图像恰好是其前身的四分之一。在输入图像$G$。上迭代该过程产生整个金字塔。
OpenCV为我们提供了一种从其前身产生每个金字塔阶段的方法: -
函数使用
1 | |
dstsize默认为图像的一半尺寸
$$
((src.cols+1)/2,(src.rows+1)/2
$$
但若设置dstsize值需要有一些严格的限制(区分了该函数和cv2.resize),具体如下:
事实上是原图像尺寸一半附近极小的区域,用于控制复杂的需要严格控制金字塔的情况,一般使用建议就不要设置整个参数了.
- 示例代码
1 | |
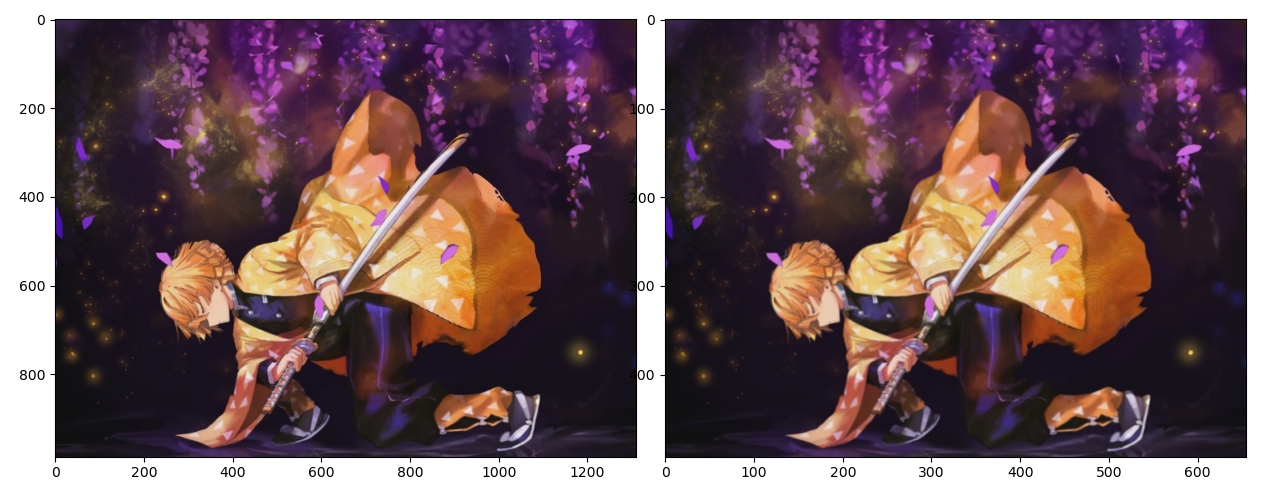
cv2.pyrDown()
上采样为图像的两倍大小
- 函数使用
1 | |
- 参数和
cv2.pyrUp类似,dstsize也同样遵循类似的限制:
- 示例代码
1 | |
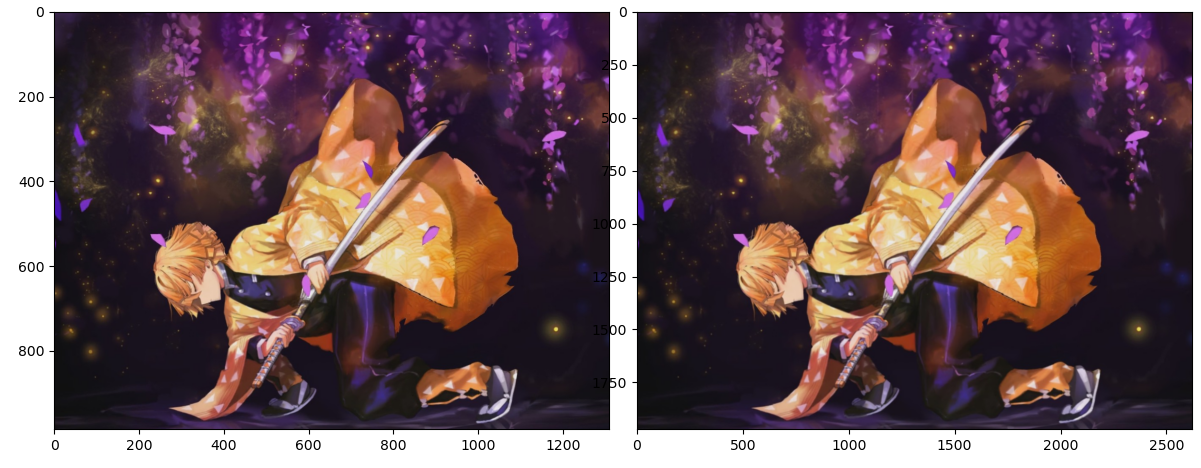
拉普拉斯金字塔
我们以前已经注意到,运算符cv2.pyrUp()不是cv2.pyrDown()的逆。这是很明显的,因为cv2.pyrDown()是一个丢失信息的操作符。为了恢复原始(较高分辨率)的图像,我们需要访问下采样过程丢弃的信息。
拉普拉斯金字塔可以认为是残差金字塔,用来存储下采样后图片与原始图片的差异。这个数据形成了拉普拉斯金字塔。拉普拉斯金字塔的第$i$层由以下关系定义:
$$
L_{i}=G_{i}-U P\left(G_{i+1}\right) \otimes g_{5 \times 5}
$$
这里,运算符$UP()$通过将原始图像中的位置$(x,y)$中的每个像素映射到目标图像中的像素$(2x+1,2y+1)$来进行大小化;符号$\otimes$表示卷积;而$g_{5×5}$是$5×5$高斯核。当然,$U P\left(G_{i+1}\right) \otimes g_{5 \times 5}$是由OpenCV提供的cv2.pyrUp()运算符的定义。因此,我们可以使用OpenCV直接计算拉普拉斯算子:
$$
L_{i}=G_{i}-pyrU P\left(G_{i+1}\right)
$$
高斯金字塔和拉普拉斯金字塔在下图中显示,这显示了从子图像恢复原始图像的逆过程。请注意拉普拉斯算子是如何实际使用高斯差异的近似值的,如之前的等式和图中示意图所示。
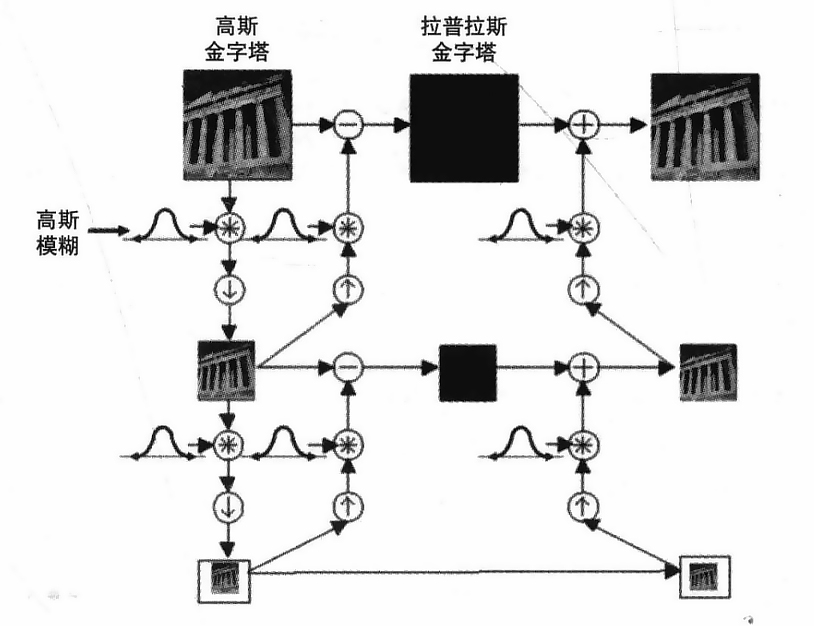
- 示例代码
1 | |
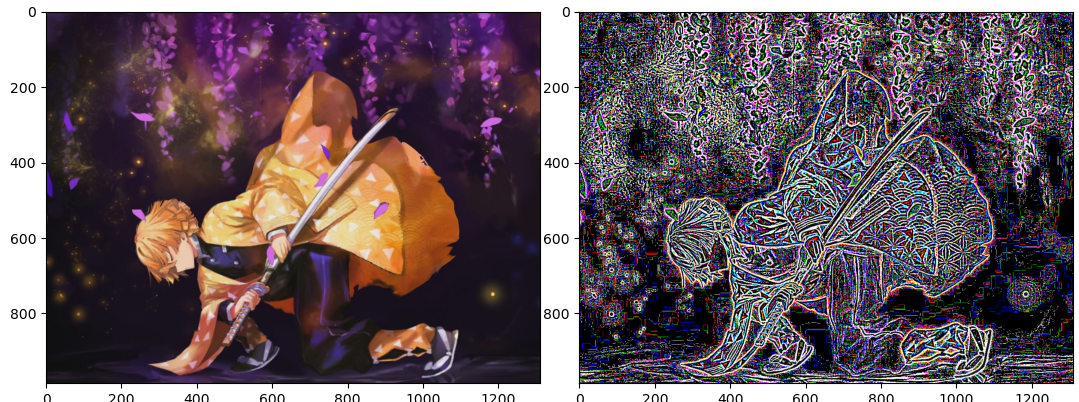
不均匀映射
在本节中,我们转向图像的几何操作,也就是说,这些变换起源于三维几何和投影几何的交叉点。这种操作包括均匀和不均匀的调整大小(后者称为“扭曲”)。执行这些操作有很多原因,例如,扭曲和旋转图像,使其可以叠加在现有场景的墙壁上,或人工放大用于目标识别的一组训练图像。可以拉伸、收缩、扭曲或旋转图像的功能称为“几何变换”。
- 对于平面区域,有两种几何变换:使用2×3矩阵的变换,称为“仿射变换”;而基于3×3矩阵进行变换,称为“透视变换”或“同形”。
- 你可以将后一种转换作为一种计算方法,用于计算一个特定观察者感觉三维平面的方法,而这些观察者可能不会直视平面。
仿射变换是可以以矩阵乘法后跟向量加法的形式表示的任何变换。在OpenCV中,代表这种转换的标准样式是2×3矩阵。定义如下:
- 很容易看出,仿射变换$A·X+B$的效果完全等同于将向量$X$扩展到向量$X’$,并且简单地将$X$的转置左乘$T$。
- 仿射变换包含 平移、旋转、侧切、缩放等功能,其中 $B$ 为平移项,其余功能由 $A$ 矩阵表示。
- 仿射变换可以如下显示:平面中的任何平行四边形$ABCD$可以通过一些仿射变换映射到任何其他平行四边形$A’B’C’D’$。如果这些平行四边形的面积不是零,隐含的仿射变换就由两个平行四边形的(三个顶点)唯一定义。如果喜欢,你可以想象一个仿射变换,将自己的图像画成一个大的橡胶片,然后通过在角上的推或拉变形来制作不同样子的平行四边形。
- 仿射变换可以将矩形转换为平行四边形。它们可以挤压形状,但必须保持两边平行。它们可以旋转或缩放它。透视变换提供更多的灵活性;透视变换可以将矩形转换为任意四边形。下图显示了各种仿射变换和透视变换的示意图。

仿射变换
仿射变换有两种情况。在第一种情况下,我们有一个想要转化的图像(或感兴趣的区域);在第二种情况下,我们有一系列点,想要计算转换的结果。这些情况在概念上非常相似,但在实际执行方面却有很大的差异。因此,对于这些情况,OpenCV有两个不同的函数。
cv2.warpAffine()
执行放射变化的函数
- 函数使用
1 | |
- 其中 $M$ 为最核心的转换矩阵,新的数据坐标由 $M$ 与原始坐标计算得到:
$$
d s t(x, y)=\operatorname{src}\left(M_{00} x+M_{01} y+M_{02}, M_{10} x+M_{11} y+M_{12}\right)
$$
- 然而,一般来说,该方程右边所示的位置可能不是整数像素。在这种情况下,需要使用插值来找到$dst(x,y)$的适当值。参数
flags用于选择插值方法。可用的插值方法和cv2.resize()中的差值方法相同 - 示例代码
1 | |

cv2.getAffineTransform()
从三对对应的点计算仿射变换。
- 函数使用
1 | |
这里的src和st是包含三个二维(x,y)点的数组。返回值是从这些点计算的仿射变换的数组。
- 示例代码
1 | |
cv2.transform()
适用于一系列点的仿射变换
- 函数使用
1 | |
当 $m.cols=src.channels()$
$$
\operatorname{dst}(I)=\mathrm{m} \cdot \operatorname{src}(I)
$$
当$ m.cols=src.channels()+1$
$$
\operatorname{dst}(I)=\mathrm{m} \cdot[\operatorname{src}(I) ; 1]
$$
- 示例代码
1 | |
cv2.invertAffineTransform()
这个函数计算一个由 2 × 3 矩阵 m 表示的仿射变换,反转仿射变换。
- 函数使用
1 | |
- 示例代码
1 | |
透视变换
透视变换是将图像从一个视平面投影到另外一个视平面的过程,所以透视变换也被称为投影映射(Projection Mapping)。我们知道在图像的仿射变换中需要变换矩阵是一个$2x3$的两维平面变换矩阵,而透视变换本质上空间立体三维变换,根据其坐标,要把三维坐标投影到另外一个视平面,就需要一个完全不同的变换矩阵M,这是透视变换跟仿射变换最大的不同。
实现原理
- 透视变换
- $ \mathrm{x}, \mathrm{y} $ 是原始图片坐标,对应得到变换后的坐标 $ x’,{y’} ,w’$,目标坐标 $ x_t=x^{\prime} / w^{\prime}, y_t=y^{\prime} / w^{\prime} $ 。
- 变换矩阵可以分为几部分理解
- $ \left[\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right] $表示线性变换
- $ \left[\begin{array}{ll}a_{31} & a_{32}\end{array}\right]_{j} $表示平移
- $ \left[\begin{array}{ll}a_{13} & a_{23}\end{array}\right]^{T} $表示透视
- 可以理解成仿射等是透视变换的特殊形式。
- 重写之前的变换公式可以得到:
cv2.warpPerspective()
实现图像的透视变换
- OpenCV 实现透视变换时 $M$ 是左乘到坐标上的,因此最终的计算公式为
$$
\operatorname{dst}(x, y)=\operatorname{src}\left(\frac{M_{11} x+M_{12} y+M_{13}}{M_{31} x+M_{32} y+M_{33}}, \frac{M_{21} x+M_{22} y+M_{23}}{M_{31} x+M_{32} y+M_{33}}\right)
$$
- 函数使用
1 | |
- 示例代码
1 | |
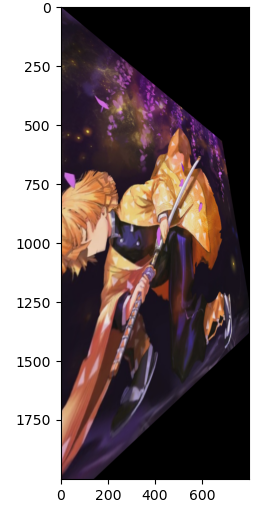
cv2.getPerspectiveTransform()
从四对相应的点计算透视变换,得到透视变换矩阵。
- 函数使用
1 | |
- 示例代码
1 | |
cv2.perspectiveTransform()
执行矢量的透视矩阵变换。
- 函数使用
1 | |
- 示例代码
1 | |
示例源码
参考资料
- 《学习 OpenCV3》 第十一章
- https://blog.csdn.net/zhangjunp3/article/details/80036310
文章链接:
https://www.zywvvd.com/notes/study/image-processing/opencv/opencv-image-trans/opencv-image-trans/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付