本文最后更新于:2024年5月7日 下午
本文摘录OpenCV 中的卷积、滤波相关操作内容,重点介绍 Opencv 操作中自定义核进行卷积的操作。
用任意线性滤波器做卷积
到目前为止,我们所接触到的卷积都是在OpenCV中API内部实现了的。学习了一些卷积操作之后,就立即联系OpenCV中实现了相应功能的函数。在调用这些函数时,函数默认地选择了某一种核,我们做的只是向函数传递一些参数来调整这个核。在OpenCV中,实际是允许我们用一个真实存在的核进行卷积操作的。
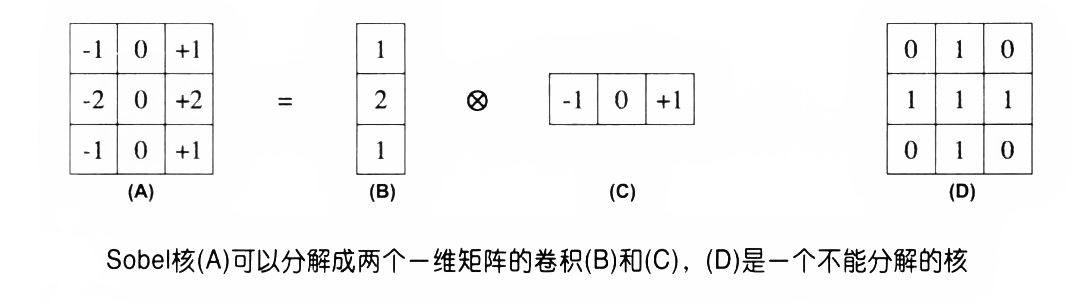
卷积核分解
理论上说,我们只要用一个数组表示一个核,然后放进一个函数,就可以用来卷积了。实际情况中,一些不起眼的地方却会在很大程度上影响到性能,可分解的矩阵通常会产生这种影响。
一个可分核可以理解成两个一维核,在卷积时先调用$x$内核,然后再调用$y$内核。两个矩阵进行卷积所产生的消耗可以用两个矩阵的面积之积近似,如此一来,用$n×n$的核对面积为$A$的图像进行卷积所需的时间时$An^2$,但如果分解成$n×1$和$1×n$的两个核,那么代价就是$An+An=2An$,因此分解卷积核可以提高提高卷积计算的效率。只要$n$不小于3,这种计算方式能提高效率,并且。随着$n$的增大,这种收益愈发明显。
cv2.filter()
官方文档
使用自定义的卷积核对图像进行卷积
1
2
3
4
5
6
7
8
9
| cv2.filter2D(
src,
ddepth,
kernel[,
dst[,
anchor[,
delta[,
borderType]]]]
) -> dst
|
1
2
3
4
5
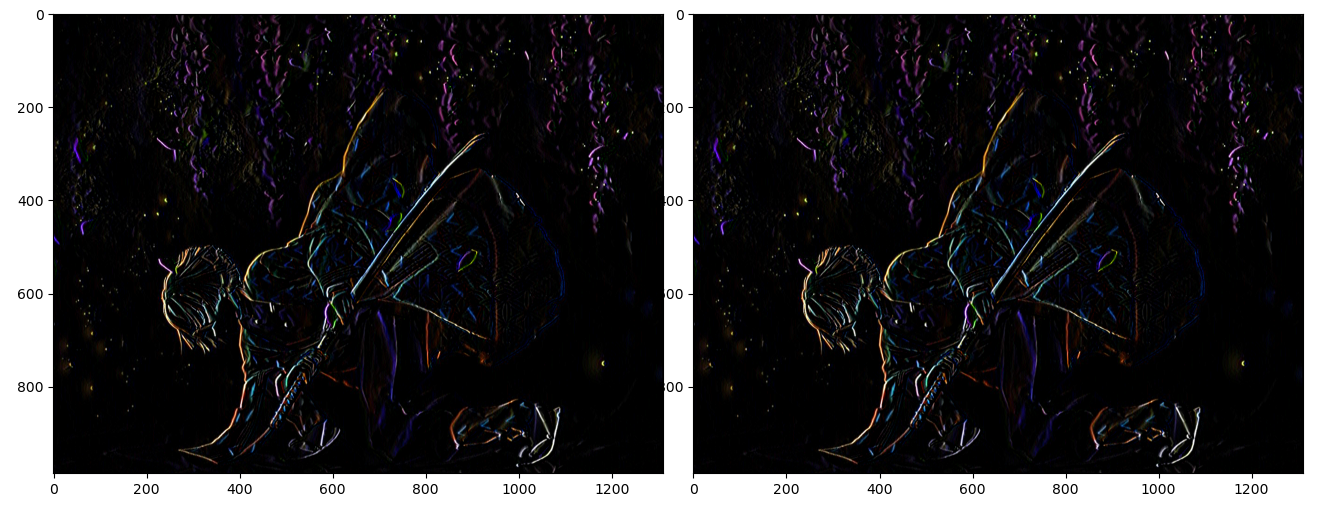
| img = mt.cv_rgb_imread('img1.jpg', gray=False)
kernal = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
sob_res = cv2.Sobel(img, -1, 1, 0, ksize=3)
cus_res = cv2.filter2D(img, -1, kernal)
PIS(sob_res, cus_res)
|
cv2.sepFilter2D
官方文档
当卷积核可分时,运算效率会得到提示,那么可以使用 cv2.sepFilter2D 函数进行卷积
1
2
3
4
5
6
7
8
9
| cv2.sepFilter2D(
src,
ddepth,
kernelX,
kernelY[,
dst[,
anchor[,
delta[,
borderType]]]] ) -> dst
|
1
2
3
4
5
6
| img = mt.cv_rgb_imread('img1.jpg', gray=False)
kernal_x = np.array([[-1, 0, 1]])
kernal_y = np.array([[1], [2], [1]])
sob_res = cv2.Sobel(img, -1, 1, 0, ksize=3)
cus_res = cv2.sepFilter2D(img, -1, kernal_x, kernal_y)
PIS(sob_res, cus_res)
|

生成卷积核
cv2.getDerivKernels()
官方文档
可以生成 Sobel 和 Scharr 的分解核
1
2
3
4
5
6
7
8
9
| cv2.getDerivKernels(
dx, # 关于 x 的导数阶。
dy, # 关于 y 的导数阶。
ksize[, # 核尺寸,可以是 1, 3, 5, 7 或 cv2.FILTER_SCHARR
kx[, # 行滤波器系数的输出矩阵,ktype 类型。
ky[, # 列滤波器系数的输出矩阵,ktype 类型。
normalize[, # 是否规范化(缩小)过滤器系数(除以面积), 如果要操作浮点图像,配置此项为True。默认为 False
ktype]]]] # 可以为 cv2.CV_32F(默认) 或 cv2.CV_64F
) -> kx, ky
|
1
2
3
4
5
6
7
8
9
10
11
| kx, ky = cv2.getDerivKernels(1, 0, 3, ktype=cv2.CV_64F)
kx
array([[-1.],
[ 0.],
[ 1.]])
ky
array([[1.],
[2.],
[1.]])
|
1
2
3
4
5
6
7
8
9
10
11
| kx, ky = cv2.getDerivKernels(1, 0, 3, normalize=True, ktype=cv2.CV_64F)
kx
array([[-0.5],
[ 0. ],
[ 0.5]])
ky
array([[0.25],
[0.5 ],
[0.25]])
|
1
2
3
4
5
6
7
8
9
10
11
| kx, ky = cv2.getDerivKernels(1, 0, cv2.FILTER_SCHARR, normalize=False, ktype=cv2.CV_64F)
kx
array([[-1.],
[ 0.],
[ 1.]])
ky
array([[ 3.],
[10.],
[ 3.]])
|
cv2.getGaussianKernel()
官方文档
用于生成 1D 高斯核
$$
G_{i}=\alpha * e^{-(i-(\mathrm{ksize}-1) / 2)^{2} /\left(2 * \operatorname{sigma}^{2}\right)}
$$
返回的核和为1
1
2
3
4
5
| cv2.getGaussianKernel(
ksize, # 核尺寸,需要是正奇数
sigma[, # 标准差
ktype] # 系数数据类型,可以为 cv2.CV_32F(默认) 或 cv2.CV_64F
) -> retval
|
其中标准差参数 sigma 可以为 None,此时:
$$
sigma =0.3 *((k s i z e-1) * 0.5-1)+0.8
$$
$$
G_{2d}=G_{1d}G_{1d}^T
$$
1
2
3
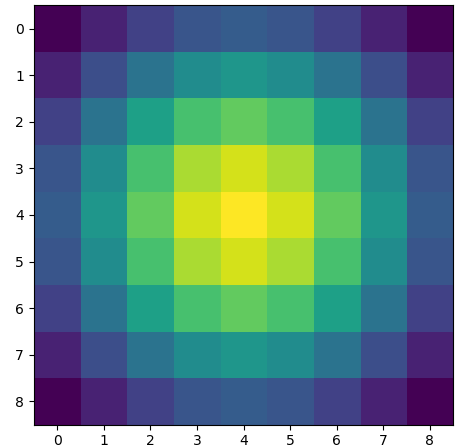
| g1d = cv2.getGaussianKernel(9, 3)
g2d = np.matmul(g1d, g1d.T)
PIS(g2d)
|
示例源码
参考资料
文章链接:
https://www.zywvvd.com/notes/study/image-processing/opencv/opencv-custom-conv/custom-conv/





