GLCM 灰度共生矩阵与 Haralick 特征

灰度共生矩阵(GLCM， Gray-level co-occurrence matrix) 是一种灰度图像纹理特征提取的方法， 是目前最常见、应用最广泛、效果最好的一种纹理统计分析方法之一， Haralick 据此定义了14种纹理特征 ，本文记录相关内容。

简介

• 灰度共生矩阵法(GLCM， Gray-level co-occurrence matrix)，就是通过计算灰度图像得到它的共生矩阵，然后透过计算该共生矩阵得到矩阵的部分特征值，来分别代表图像的某些纹理特征 (纹理的定义仍是难点) 的方法。
• 灰度共生矩阵能反映图像灰度关于方向、相邻间隔、变化幅度等综合信息，它分析图像的是图像局部模式和它们排列规则的基础。

GLCM 灰度共生矩阵

定义

• 灰度共生矩阵是一个统计描述影像中的一个局部区域或整个区域相邻象元或一定间距内两象元灰度呈现某种关系的矩阵。
• 该矩阵中的元素值代表灰度级之间联合条件概率密度 $P(i,j|d,θ) $，表示在 给定空间距离 $d$ 和方向 $θ$ 时，灰度以 $i$ 为始点，出现灰度级为 $j$ 的概率。
• 算例：

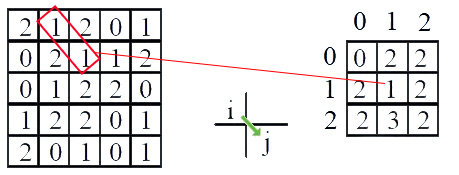
左边是一幅 $5 \times 5$ 的图像，其中灰阶为 ${0,1,2}$，三阶灰度，因此共生矩阵维度为 $3 \times 3$，在定义好向量方向后，统计图像中按照向量方向产生的数据对，将数据对的总数量填入共生矩阵的对应位置。

• 共生矩阵数学表示：

$$ \mathbf{G}=\left[\begin{array}{cccc}p(1,1) & p(1,2) & \cdots & p\left(1, N_{g}\right) \\ p(2,1) & p(2,2) & \cdots & p\left(2, N_{g}\right) \\ \vdots & \vdots & \ddots & \vdots \\ p\left(N_{g}, 1\right) & p\left(N_{g}, 2\right) & \cdots & p\left(N_{g}, N_{g}\right)\end{array}\right] $$

$p(i,j)$ 是通过计算一个值为 $i$ 的像素与值为 $j$ 的像素相邻的次数，然后将整个矩阵除以所进行比较的总次数而产生的。

• 统计方向，常用的统计方向为像素的 8 邻域方向：

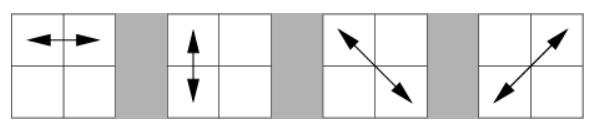
相关概念

• 共生矩阵的大小

  在不对原图像灰度级别进行压缩的情况下，共生矩阵的大小为原图像灰度的级数的平方；

  在实际应用中，从纹理特征的计算效率以及共生矩阵的存储方面考虑，通常先把原始图像的灰度等级进行压缩比如从灰度级别为 0-255 的 8bit 图像压缩为灰度级别为 0-31的 5bit 图像，相应的共生矩阵的维数从 $256\times256$ 降低到 $32 \times32 $

• 基准窗口

  当前像素为中心的某一个窗口，尺寸通常为奇数方阵，大小可设为$3 \times3$,$5 \times5 $,$7 \times7 $等

• 移动窗口

以基准窗口为参考窗口，通过设定的移动方向和步长进行移动的窗口。尺寸大小与基准窗口的一样，位置由移动方向与步长决定

• 移动方向

  基准窗口与移动窗口的相对方向。移动方向可以任意设定，通常为0°，45°，90°，135°

• 移动步长

  基准窗口中心像元和移动窗口中心像元的距离 (用像素表示)

特点

1. 共生矩阵是一个方阵， 该方阵的大小取决于原始图像灰度的级数，与原始图像尺度大小无关
2. 共生矩阵与统计方向和距离有关
3. 矩阵元素值的分布与图像的信息丰富程度密切相关：如果灰度共生矩阵非零元素集中在主对角线上，则说明图像信息量在该方向上低，如果非零元素值在非主对角线上离散分布，说明在该方向上图像灰度变化频繁，信息量大。
4. 共生矩阵元素值的大小相对于主对角线的分布与图像的纹理粗细程度密切相关：移动步长一定，如果靠近主对角线的元素值较大，则图像的纹理比较粗糙，反之，如果离主对角线较远的元素值较大，则表明图像的纹理较细。即灰度共生矩阵元素相对于主对角线的分布情况反映图像纹理的粗细程度。

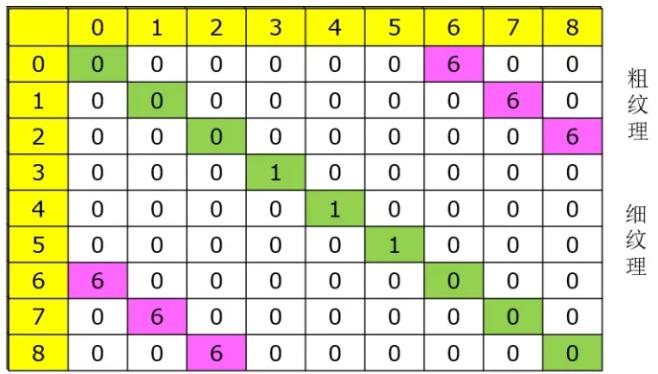
5. 基于GLCM的纹理分析需要综合考虑以下几个因素：
6. 图像的灰度级
7. 光谱波段
8. 不同特征值选择
9. 移动方向
10. 窗口大小和移动步长（基于像素GLCM计算中）

示例

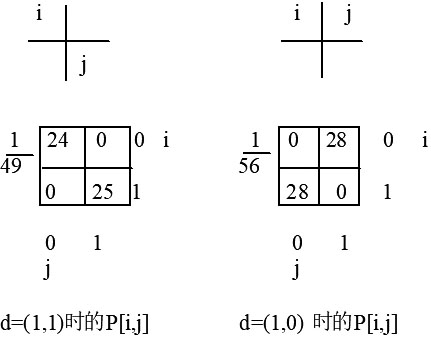
• 棋盘格图像：

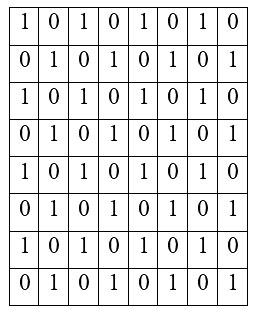
• 定义两种方向 $d$ 后，计算共生矩阵：

Haralick 特征

• 灰度共生矩阵提供了影像灰度方向、间隔和变化幅度的信息，但它并不能直接提供区别纹理的特性，因此需要在灰度共生矩阵的基础上提取用来定量描述纹理特征的统计属性。
• Haralick定义了14种纹理特征。

• 常用的特征统计量主要有: 均值(Mean) 、方差(Variance) 、同质性(Homogeneity)、对比度 (Contrast)、非相似性 (Dissimilarity)、熵 (Entropy )、角二阶矩( Angular Second Moment )、相关性 ( Correlation ) 等。

均值 (Mean)

• 均值反映纹理的规则程度，纹理杂乱无章、难以描述的，值较小；规律性强、易于描述的，值较大
• 公式：

$$
Mean =\sum_{i} \sum_{j} p(i, j)· i
$$

方差 (Variance)

• 方差、标准差反映像元值与均值偏差的度量，当图像中灰度变化较大时，方差、标准差值较大。

• 公式

$$
Variance =\sum_{i} \sum_{j} p(i, j)· (i-Mean)^2
$$

标准差 (Std)

• 方差、标准差反映像元值与均值偏差的度量，当图像中灰度变化较大时，方差、标准差值较大。
• 公式：

$$
Std = \sqrt{Variance}
$$

同质度 (Homogeneity)

• 也叫 **inverse difference moment (逆差距) **，是图像局部灰度均匀性的度量，如果图像局部的灰度均匀，同质度取值较大。
• 公式：

$$
Homogeneity=\sum_{i} \sum_{j} \frac{1}{1+(i-j)^{2}} p(i, j)
$$

对比度 (Contrast)

• 反映图像中局部灰度变化总量。在图像中，如局部像素对的灰度差别越大，则图像的对比度越大，图像的视觉效果越清晰。
• 公式

$$
Contrast=\sum_{i=1}^{N_{s}} \sum_{j=1}^{N_{s}} p(i, j) (i-j)^2
$$

非相似性 (Dissimilarity)

• 度量与对比度相类似，但是是线性增加。如果局部的对比度越高，则非相似度也越高。

• 公式：

$$
Dissmilarity =\sum_{i} \sum_{j} p(i, j){·}|i-j|
$$

熵 (Entropy)

• 是图像所具有的信息量的度量，是测量灰度级分布随机性的特征参数，表征了图像中纹理的复杂程度。图像的纹理越复杂，熵值越大；反之，图像中的灰度越均匀，则熵值就越小。
• 公式：

$$
Entropy =-\sum_{i} \sum_{j} p(i, j){·} \ln p(i, j)
$$

角二阶矩 ( Angular Second Moment )

• 也叫能量，是图像灰度分布均匀性的度量。当GLCM中元素分布较集中于主对角线附近时，说明局部区域内图像灰度分布较均匀，ASM取值相应较大；相反，如果共生矩阵的所有值均相等，则ASM值较小。

• 公式：

$$
ASM = \sum_{i} \sum_{j} p(i, j)^{2}
$$

相关性（Correlation）

• 描述 GLCM 中行或列元素之间的相似程度的，它反映某种灰度值沿某方向的延伸长度，若延伸的越长，则相关性越大，它是灰度线性关系的度量。
• 公式：

$$ Correlation =\sum_{i} \sum_{j} \frac{(i-\text { Mean }) (j-\text { Mean }) p(i, j)^{2}}{\text { Variance }} $$

参考资料

• https://zhuanlan.zhihu.com/p/429391655
• https://zhuanlan.zhihu.com/p/90235253
• https://zhuanlan.zhihu.com/p/110228230
• https://murphylab.web.cmu.edu/publications/boland/boland_node26.html

文章链接：
https://www.zywvvd.com/notes/study/image-processing/feature-extraction/image-glcm/image-glcm/