本文最后更新于:2024年5月7日 下午
Gabor 变换是一种短时加窗Fourier变换,本文记录相关内容。
简介
- Fourier 变换是一种信号处理的有力工具,可以将图像从空域转换到频域,并提取到空域上不易提取到的特征。但是Fourier变换缺乏时间和位置的局部信息。
- Gabor 变换是一种短时加窗Fourier变换(简单理解起来就是在特定时间窗内做Fourier变换),是短时傅里叶变换中窗函数取为高斯函数时的一种特殊情况。因此,Gabor滤波器可以在频域上不同尺度、不同方向上提取相关的特征。另外,Gabor函数与人眼的作用相仿,所以经常用作纹理识别上,并取得了较好的效果。
- 在二维空间中,使用一个三角函数(a)(如正弦函数)与一个高斯函数(b)叠加,我们得到了一个Gabor滤波器©。
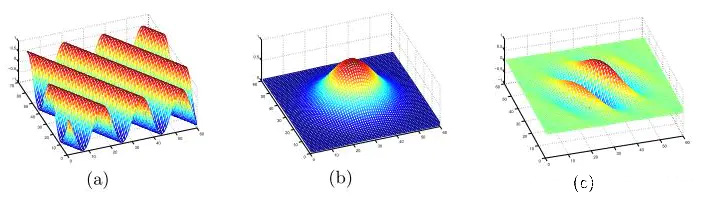
Gabor 滤波
公式定义
$$
g(x, y ; \lambda, \theta, \psi, \sigma, \gamma)=\exp \left(-\frac{x^{\prime 2}+\gamma^{2} y^{\prime 2}}{2 \sigma^{2}}\right) \exp \left(i\left(2 \pi \frac{x^{\prime}}{\lambda}+\psi\right)\right)
$$
$$
g(x, y ; \lambda, \theta, \psi, \sigma, \gamma)=\exp \left(-\frac{x^{\prime 2}+\gamma^{2} y^{\prime 2}}{2 \sigma^{2}}\right) \cos \left(2 \pi \frac{x^{\prime}}{\lambda}+\psi\right)
$$
$$
g(x, y ; \lambda, \theta, \psi, \sigma, \gamma)=\exp \left(-\frac{x^{\prime 2}+\gamma^{2} y^{\prime 2}}{2 \sigma^{2}}\right) \sin \left(2 \pi \frac{x^{\prime}}{\lambda}+\psi\right)
$$
$$
\begin{array}{l}
x^{\prime}=x \cos \theta+y \sin \theta \\ y^{\prime}=-x \sin \theta+y \cos \theta
\end{array}
$$
| 参数 |
简介 |
含义 |
| $\lambda$ |
波长 |
表示正弦因子的波长,它的值以像素为单位制定,通常大于等于2,但不能大于输入图像尺寸的1/5. |
| $\theta$ |
方向 |
表示法线到 Gabor 函数的平行条纹的方向 |
| $\phi$ |
相位偏移 |
相位偏移 |
| $\sigma$ |
标准差 |
高斯分布的标准差 |
| $\gamma$ |
长宽比 |
空间纵横比,指定 Gabor 函数支持的椭圆度 |
提取图像特征
- 一组具有不同频率和方向的 Gabor 滤波器可能有助于从图像中提取有用的特征。
- 在离散域中,二维 Gabor 滤波器表示为:
$$
\begin{array}{l}
G_{c}[i, j]=B e^{-\frac{\left(i^{2}+j^{2}\right)}{2 \sigma^{2}}} \cos (2 \pi f(i \cos \theta+j \sin \theta)) \\
G_{s}[i, j]=C e^{-\frac{\left(i^{2}+j^{2}\right)}{2 \sigma^{2}}} \sin (2 \pi f(i \cos \theta+j \sin \theta))
\end{array}
$$
其中 B 和 C 是要确定的标准化因子。
| 参数 |
含义 |
| $f$ |
定义在纹理中查找的频率。 |
| $ \theta$ |
查找纹理的方向 |
| $\sigma$ |
标准差,可以调整被分析图像区域的尺寸 |
应用示例
Python 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| import cv2
import numpy as np
import matplotlib.pyplot as plt
def Gabor_filter(K_size=111, Sigma=10, Gamma=1.2, Lambda=10, Psi=0, angle=0):
d = K_size // 2
gabor = np.zeros((K_size, K_size), dtype=np.float32)
for y in range(K_size):
for x in range(K_size):
px = x - d
py = y - d
theta = angle / 180. * np.pi
_x = np.cos(theta) * px + np.sin(theta) * py
_y = -np.sin(theta) * px + np.cos(theta) * py
gabor[y, x] = np.exp(-(_x**2 + Gamma**2 * _y**2) / (2 * Sigma**2)) * np.cos(2*np.pi*_x/Lambda + Psi)
gabor /= np.sum(np.abs(gabor))
return gabor
As = [0, 45, 90, 135]
plt.subplots_adjust(left=0, right=1, top=1, bottom=0, hspace=0, wspace=0.2)
for i, A in enumerate(As):
gabor = Gabor_filter(K_size=111, Sigma=10, Gamma=1.2, Lambda=10, Psi=0, angle=A)
out = gabor - np.min(gabor)
out /= np.max(out)
out *= 255
out = out.astype(np.uint8)
plt.subplot(1, 4, i+1)
plt.imshow(out, cmap='gray')
plt.axis('off')
plt.title("Angle "+str(A))
plt.savefig("out.png")
plt.show()
|

OpenCV 实现
函数定义
1
| cv.getGaborKernel( ksize, sigma, theta, lambd, gamma[, psi[, ktype]] ) -> retval
|
| 参数 |
含义 |
| ksize |
返回的筛选器大小。 |
| sigma |
高斯分布标准差。 |
| theta |
Gabor 函数法向平行条纹的方向。 |
| lambd |
正弦因子波长。 |
| gamma |
空间长宽比,表示椭圆形状。 |
| psi |
相位偏移。 |
| ktype |
滤波器系数的类型。它可以是 CV_32F 或 CV_64F。 |
- OpenCV 中
getGaborKernel 函数的代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| cv::Mat cv::getGaborKernel( Size ksize, double sigma, double theta,
double lambd, double gamma, double psi, int ktype )
{
double sigma_x = sigma;
double sigma_y = sigma/gamma;
int nstds = 3;
int xmin, xmax, ymin, ymax;
double c = cos(theta), s = sin(theta);
if( ksize.width > 0 )
xmax = ksize.width/2;
else
xmax = cvRound(std::max(fabs(nstds*sigma_x*c), fabs(nstds*sigma_y*s)));
if( ksize.height > 0 )
ymax = ksize.height/2;
else
ymax = cvRound(std::max(fabs(nstds*sigma_x*s), fabs(nstds*sigma_y*c)));
xmin = -xmax;
ymin = -ymax;
CV_Assert( ktype == CV_32F || ktype == CV_64F );
Mat kernel(ymax - ymin + 1, xmax - xmin + 1, ktype);
double scale = 1;
double ex = -0.5/(sigma_x*sigma_x);
double ey = -0.5/(sigma_y*sigma_y);
double cscale = CV_PI*2/lambd;
for( int y = ymin; y <= ymax; y++ )
for( int x = xmin; x <= xmax; x++ )
{
double xr = x*c + y*s;
double yr = -x*s + y*c;
double v = scale*std::exp(ex*xr*xr + ey*yr*yr)*cos(cscale*xr + psi);
if( ktype == CV_32F )
kernel.at<float>(ymax - y, xmax - x) = (float)v;
else
kernel.at<double>(ymax - y, xmax - x) = v;
}
return kernel;
}
|
特征提取示例
1
2
3
4
5
6
7
8
| import mtutils as mt
import cv2 as cv
retval = cv.getGaborKernel(ksize=(111,111), sigma=10, theta=60, lambd=10, gamma=1.2)
image1 = mt.cv_rgb_imread('test.jpg')
result = cv.filter2D(image1,-1,retval)
mt.PIS([image1, 'origin image'], [result, 'gabor image'])
|
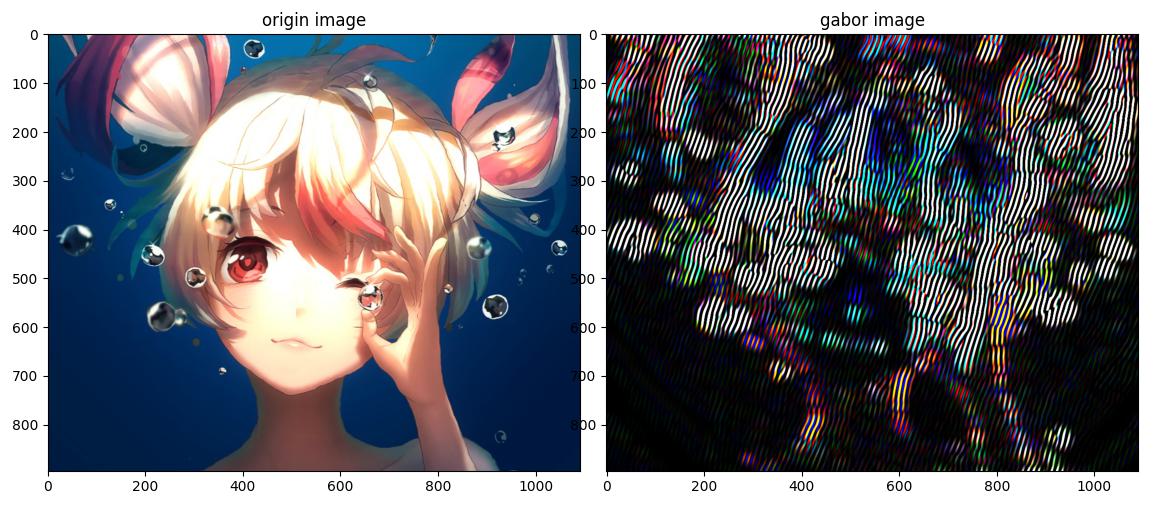
斑马线检测示例

-
检测代码
需要安装库 mtutils pip install mtutils
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| import mtutils as mt
import numpy as np
import cv2 as cv
image = mt.cv_rgb_imread('bmx.jpg', 1)
kernel_size = (5, 5)
sigma = 1
lambd = np.pi / 2
gamma = 0.5
psi = 0
theta_list = [0, np.pi * 0.25, np.pi * 0.5, np.pi * 0.75]
sum_result = np.zeros_like(image, dtype='float32')
kernel_list = list()
result_list = list()
for theta in theta_list:
kernel = cv.getGaborKernel(kernel_size, sigma, theta, lambd, gamma, psi)
kernel_list.append(kernel)
result = cv.filter2D(image, -1, kernel)
result_list.append(result)
sum_result += result
mt.PIS(*kernel_list, row_num=1)
mt.PIS([result_list[0], '0°'], [result_list[1], '45°'], [result_list[2], '90°'], [result_list[3], '135°'], [sum_result, 'fea_sum'], row_num=1, axis_off=True)
dst = cv.convertScaleAbs(sum_result, alpha=0.2, beta=0)
_, thr_res = cv.threshold(dst, 0, 255, cv.THRESH_BINARY_INV | cv.THRESH_OTSU)
mt.PIS(255 - thr_res)
pass
|
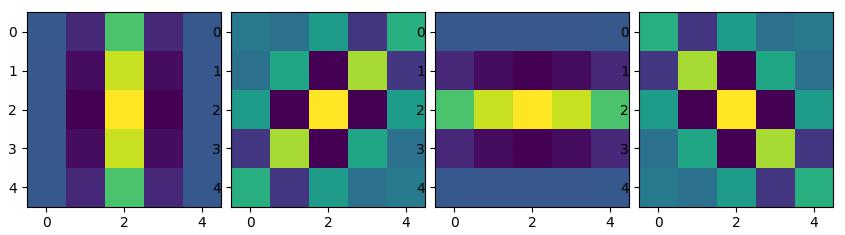


参考资料
文章链接:
https://www.zywvvd.com/notes/study/image-processing/feature-extraction/gabor-filter/gabor-filter/








