本文最后更新于:2024年5月7日 下午
cv.goodFeaturesToTrack()提取到的角点只能达到像素级别, 在很多情况下并不能满足实际的需求,这时,我们则需要使用cv.cornerSubPix()对检测到的角点作进一步的优化计算,可使角点的精度达到亚像素级别。
检测
前面已经提及 goodFeaturesToTrack() 提取到的角点 只能达到像素级别,获取的角点坐标是整数,但是通常情况下,角点的真实位置并不一定在整数像素位置,因此为了获取更为精确的角点位置坐标,需要角点坐标达到亚像素(subPixel)精度。这时,我们则需要使用cv::cornerSubPix()对检测到的角点作进一步的优化计算,可使角点的精度达到亚像素级别。
原理解析
在亚像素级精度的角点检测算法中,一种方法是从亚像素角点到周围像素点的矢量应垂直于图像的灰度梯度这个观察事实得到的,通过最小化误差函数的迭代方法来获得亚像素级精度的坐标值。

对于一个角点 $ q $ ,考虑在 $ q $ 附近的窗口 win 内的任意点 $ p $ 。 $ p $ 的图像梯度与向量 $ q-p $ 的点积总是为零。
原因是如果 $ p $ 在平坦区域,则 $ p $ 的梯度 为零,如果 $ p $ 在边缘处, $ p $ 的梯度总是与 $ q-p $ 垂直。
据此可以列出公式:
$$ \begin{array}{c} I_{x}(p)\left(x_{q}-x_{p}\right)+I_{y}(p)\left(y_{q}-y_{p}\right)=0 \\ I_{x}(p) x_{q}+I_{y}(p) y_{q}=I_{x}(p) x_{p}+I_{y}(p) y_{p} \end{array} $$联立窗口 win内的所有点 $ p_{i} $ 得到方程组,写成矩阵形式如下:
$$ \left(\begin{array}{cc}I_{x}\left(p_{1}\right) & I_{y}\left(p_{1}\right) \\ \vdots & \vdots \\ I_{x}\left(p_{n}\right) & I_{y}\left(p_{n}\right)\end{array}\right)\left(\begin{array}{c}x_{q} \\ y_{q}\end{array}\right)=\left(\begin{array}{c}I_{x}\left(p_{1}\right) x_{p_{1}}+I_{y}\left(p_{1}\right) y_{p_{1}} \\ \vdots \\ I_{x}\left(p_{n}\right) x_{p_{n}}+I_{y}\left(p_{n}\right) y_{p_{n}}\end{array}\right) $$这是一个超约束(over-constrained)线性方程组,可以用最小二乘法求最佳解。
$$ A=\left(\begin{array}{cc}I_{x}\left(p_{1}\right) & I_{y}\left(p_{1}\right) \\ \vdots & \vdots \\ I_{x}\left(p_{n}\right) & I_{y}\left(p_{n}\right)\end{array}\right), b=\left(\begin{array}{c}I_{x}\left(p_{1}\right) x_{p_{1}}+I_{y}\left(p_{1}\right) y_{p_{1}} \\ \vdots \\ I_{x}\left(p_{n}\right) x_{p_{n}}+I_{y}\left(p_{n}\right) y_{p_{n}}\end{array}\right) $$ $$ \begin{array}{c} A^{T} A\left(\begin{array}{l}x_{q} \\ y_{q}\end{array}\right)=A^{T} b \\ A^{T} A=\left(\begin{array}{cc}\sum I_{x}^{2} & \sum I_{x} I_{y} \\ \sum I_{x} I_{y} & \sum I_{y}^{2}\end{array}\right) \\ A^{T} b=\left(\begin{array}{l}\sum I_{x}^{2} x+\sum I_{x} I_{y} y \\ \sum I_{x} I_{y} x+\sum I_{y}^{2} y\end{array}\right) \\ \left(\begin{array}{l}x_{q} \\ y_{q}\end{array}\right)=\left(A^{T} A\right)^{-1} A^{T} b \end{array} $$或直接沿用伪逆求解最小二乘解的结论:
$$ \left(\begin{array}{l}x_{q} \\ y_{q}\end{array}\right)= A^{+} b $$然后以新的 $ \left(x_{q}, y_{q}\right) $ 为初始角点,重新执行以上优化过程,反复迭代,直至 $ \left(x_{q}, y_{q}\right) $ 收敛。
OpenCV 函数
函数定义:
1 | |
参数详解:
| 参数 | 含义 |
|---|---|
| image | 输入图像,和 cv::goodFeaturesToTrack() 中的输入图像是同一个图像。 |
| corners | 检测到的角点,即是输入也是输出。 |
| winSize | 计算亚像素角点时考虑的区域的大小,大小为NXN; N=(winSize*2+1)。 |
| zeroZone | 作用类似于winSize,但是总是具有较小的范围,通常忽略(即Size(-1, -1))。 |
| criteria | 表示计算亚像素时停止迭代的标准,可选的值有cv::TermCriteria::MAX_ITER 、cv::TermCriteria::EPS(可以是两者其一,或两者均选),前者表示迭代次数达到了最大次数时停止,后者表示角点位置变化的最小值已经达到最小时停止迭代。二者均使用 cv::TermCriteria()构造函数进行指定。 |
cornerSubPix 的实现中 :
-
随着角点位置的细化,每次迭代都要重新计算窗口的像素值。由于中心坐标并非整数,因此整个窗口的像素坐标也不是整数,需要用插值算法来计算每个点的像素值
-
使用加权最小二乘法优化结果,用高斯核让算法给离中心近的点更高的权重
Python 实现
示例图像:

示例代码:
1 | |
输出亚像素角点结果:
1 | |
绘制图像:
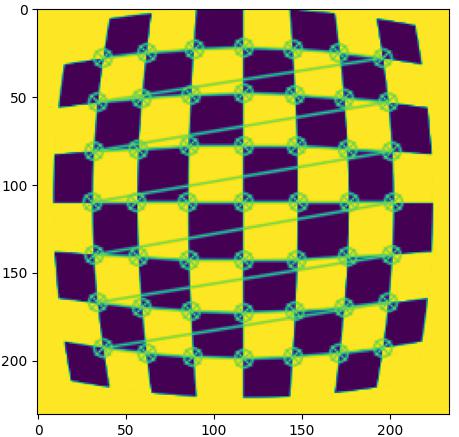
参考资料
- https://blog.csdn.net/qq_28584889/article/details/103356855
- https://blog.csdn.net/hhyh612/article/details/79189983
- https://www.cnblogs.com/riddick/p/8476456.html
文章链接:
https://www.zywvvd.com/notes/study/image-processing/corner-det/corner-subpix/corner-subpix/
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付